Spesso si sente usare l’aggettivo “esponenziale” come sinonimo di “molto” o di “veloce” (una certa “quantità esponenziale” o una certa “crescita esponenziale”), non solo tra amici o conoscenti ma anche in contesti più istituzionali. La BBC ha parlato della percezione che le persone hanno del senso della parola “esponenziale” in un articolo del 13 agosto relativamente alla crescita esponenziale dei casi di Covid-19. Questa fase dell’epidemia di coronavirus in Italia è caratterizzata dall’evoluzione esponenziale dei contagi e della frequenza dei positivi al test per la presenza del virus. Inoltre, le vacanze estive hanno indotto una crescita esponenziale dei contagi in regioni che erano in crescita lineare e un'accelerazione della crescita esponenziale in regioni dove la crescita era già di questo tipo.

Crescita esponenziale

Anzitutto bisogna inserire il concetto di crescita esponenziale in un contesto temporale, appunto, di crescita nel tempo. La differenza con la crescita lineare è che quest’ultima, se rappresentata in un piano cartesiano, è descritta da una linea retta (più o meno pendente), mentre la crescita esponenziale è descritta da una curva la cui pendenza in ciascun punto cresce nel tempo proporzionalmente al valore della curva in quel punto. Un parametro che si prende in considerazione per descrivere la velocità di una crescita esponenziale è il tempo di raddoppio: il tempo necessario a raddoppiare un certo valore, parametro che resta costante se non cambia il tipo di crescita esponenziale. Più è piccolo il valore del tempo di raddoppio e più velocemente cresce la curva.

Per capirci: se in una crescita lineare ci vogliono otto giorni per passare da 10 a 20 contagi, ce ne vorranno sedici per passare da 20 a 40. In una crescita esponenziale, se ci vogliono otto giorni per passare da 10 contagi a 20, ce ne vogliono sempre otto per passare da 20 a 40 e da 40 a 80 ma anche otto giorni per passare da 320 a 640 contagi, lo stesso aumento che nella crescita lineare di prima avviene in ben duecentocinquantasei giorni.

Come racconta la BBC, uno studio ha evidenziato che più tra le persone c’è difficoltà nel capire la velocità della crescita esponenziale dei contagi da Covid-19, meno si tende a rispettare le misure di contenimento della diffusione. Ecco, quindi, che capire questo semplice concetto matematico diventa molto importante – e prima lo si impara (a scuola) meglio è. Ma, come diceva negli anni ‘60 il maestro Alberto Manzi, “non è mai troppo tardi”.

Un altro esempio significativo di crescita esponenziale (e di gravità sottostimata del problema) è l’aumento – esponenziale, per l’appunto – della concentrazione di anidride carbonica in atmosfera negli ultimi 100 anni circa per causa umana.

Accelerazione da vacanze: crescita dei contagi da lineare a esponenziale

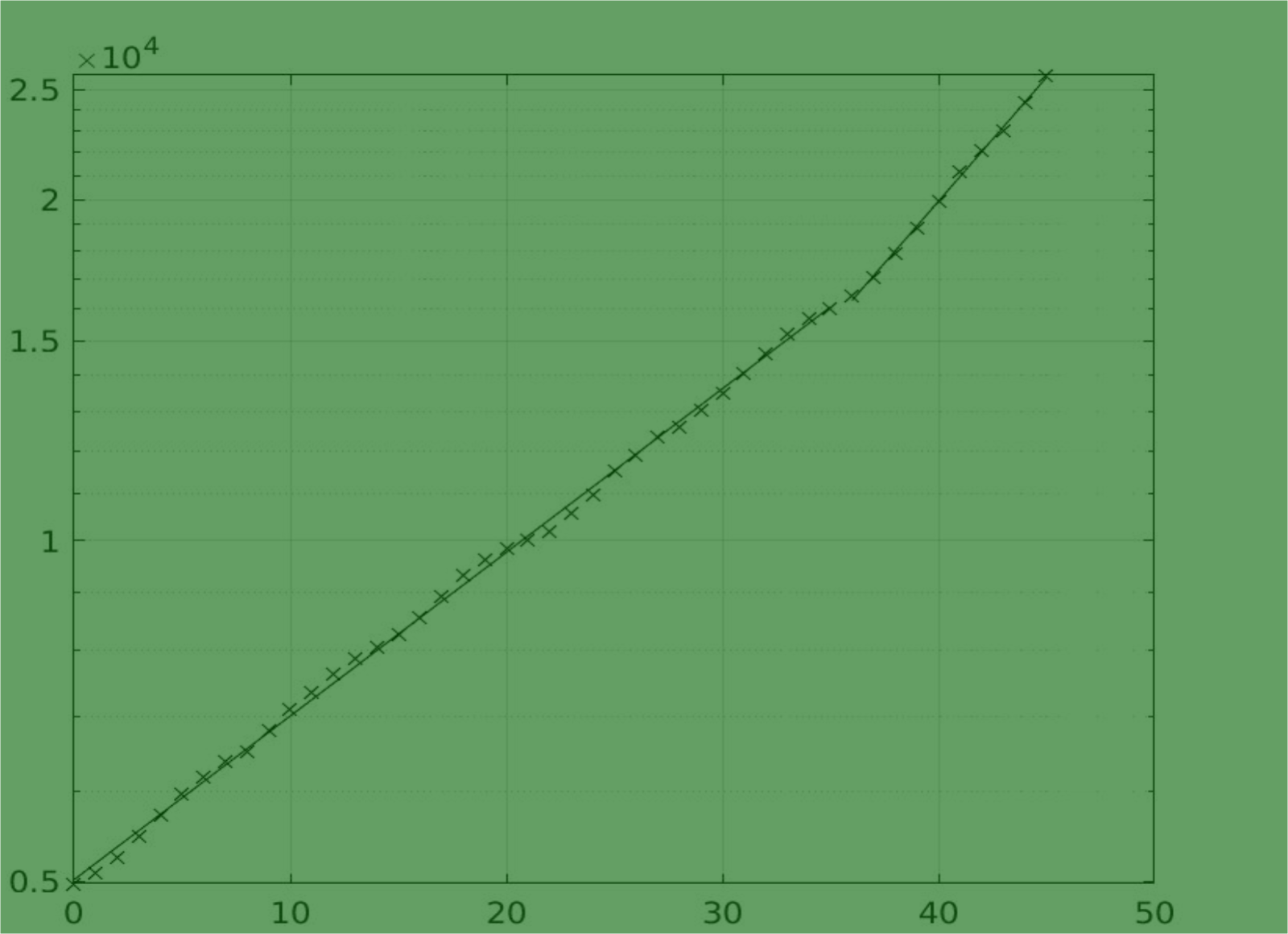
Come si può vedere nella seguente Figura 1, i contagi nella regione Emilia-Romagna dal 13 luglio al 27 agosto 2020 hanno seguito prima una crescita lineare che poi si è trasformata poco dopo metà agosto in esponenziale con tempo di raddoppio pari a circa 8 giorni.

Figura 1 Crescita del numero totale dei casi della regione Emilia-Romagna dal 13 luglio al 27 agosto 2020. È evidente dalle curve di regressione che la crescita, poco dopo metà agosto, è divenuta esponenziale da lineare.

Guardando il grafico della Sardegna, invece, si nota come una crescita esponenziale con tempo di raddoppio di circa 10 giorni, si sia trasformata in una crescita esponenziale più rapida, con tempo di raddoppio pari a circa 2 giorni, che rallenta un poco successivamente passando a un tempo di raddoppio di circa 3 giorni. I cambiamenti del tempo di raddoppio si notano meglio osservando la variazione del numero totale dei casi in scala logaritmica (in cui le curve esponenziali diventano rette). In altre parole, la crescita resta esponenziale ma, rispetto alla prima fase, diminuisce il tempo di raddoppio (questa variazione, nel grafico logaritmico, salta all'occhio immediatamente).

Figura 2 Numero totale dei casi dal 13 luglio al 27 agosto 2020 in Sardegna. Da poco dopo metà agosto la crescita esponenziale diventa più veloce. Negli ultimi quattro giorni notiamo un leggero aumento del tempo di raddoppio.

Figura 3 La variazione del numero totale dei casi della Sardegna in scala logaritmica denota, circa da poco dopo metà agosto, una diminuzione del tempo di raddoppio della crescita esponenziale. Negli ultimi quattro giorni notiamo un leggero aumento del tempo di raddoppio.

Ecco anche i due grafici relativi alla diminuzione del tempo di raddoppio in Italia, cioè sommando tutti i contributi a livello nazionale. I tempi di raddoppio nella prima e seconda fase sono 21 e 12 giorni rispettivamente.

Figura 4 Numero totale dei casi dal 13 luglio al 27 agosto 2020 in Italia. Poco dopo metà agosto la crescita esponenziale diventa più veloce.

Figura 5 Variazione, in scala logaritmica, del numero totale dei casi in Italia dal 13 luglio al 27 agosto 2020. Poco dopo metà agosto si nota l’aumento di pendenza.

Riportiamo anche il grafico del Veneto, in cui durante la crescita non cambia tempo di raddoppio, ma è comunque esponenziale (e non lineare!). Il tempo di raddoppio, in questo caso, è uguale a 18 giorni circa.

Figura 6 Numero totale dei casi dal 13 luglio al 27 agosto 2020 in Veneto. Si nota una crescita di tipo esponenziale.

Figura 7 Variazione, in scala logaritmica, del numero totale dei casi in Veneto dal 13 luglio al 27 agosto 2020. Si nota una crescita di tipo esponenziale.

Infine, nella Figura 8 vediamo l’andamento in scala logaritmica dal 13 luglio al 27 agosto del rapporto tra il numero di nuovi casi positivi al giorno in Italia e il corrispondente numero di tamponi. Come si può osservare, i dati mostrano evidenza di una crescita lineare in scala logaritmica, il che implica crescita esponenziale nella scala originaria.

Figura 8 Andamento in scala logaritmica, del rapporto tra il numero dei nuovi casi positivi giornalieri dal 13 luglio al 27 agosto 2020 e il corrispondente numero di tamponi. Si nota una crescita di tipo lineare, che implica una crescita esponenziale nella scala originaria.