La dinamica delle folle ha stimolato in tempi recenti l'interesse dei matematici applicati. Ciò è avvenuto soprattutto in conseguenza di eventi di grande portata, spesso catastrofici, che hanno fatto capire l'importanza di affiancare ai tradizionali metodi di indagine scientifica, quali l'osservazione sperimentale, strumenti di simulazione e predizione.
Emblematico è il caso del London Millennium Bridge, un ponte pedonale sul Tamigi chiuso due giorni dopo la sua inaugurazione nel 2000 a causa di forti oscillazioni laterali che compromettevano la sicurezza dei passanti. Approfondite (e costose) analisi supplementari accertarono che le instabilità erano dovute a fenomeni di risonanza innescati dagli stessi pedoni. Il ponte venne definitivamente riaperto due anni più tardi, ma le sue vicissitudini resero evidente la necessità di studiare l'accoppiamento folla-struttura in fase di progettazione di infrastrutture pedonali.

Ponte Jamarat
durante un pellegrinaggio
Un altro esempio significativo è il ponte delle Jamarat a Mina, una città dell'Arabia del Sud vicino a La Mecca, annualmente meta del Hajj, il pellegrinaggio che i musulmani fisicamente ed economicamente abili devono compiere almeno una volta nella vita. L'elevato numero di pellegrini che affollano il ponte in quelle occasioni ha provocato, negli anni Novanta, la morte di numerose persone schiacciate dalla folla. I modelli matematici hanno aiutato a studiare la dinamica del flusso di pellegrini, suggerendo contromisure per migliorare la sicurezza dell'evento.
Anche senza chiamare in causa eventi così importanti, si può fare quotidianamente esperienza di luoghi affollati: centri commerciali, stazioni, aeroporti, stadi, nella cui progettazione rientra sempre più spesso la simulazione virtuale. Essa consente infatti di studiare ambienti che rispondano ai necessari criteri di sicurezza per i loro frequentatori, senza costruirli veramente se non in ultima battuta.
Costruire un modello matematico
La costruzione di un modello per il moto di folle richiede di descrivere con il linguaggio della matematica un sistema fortemente non standard. Infatti i pedoni obbediscono solo in minima parte alle leggi della meccanica newtoniana e per il resto sono capaci di prendere decisioni e di auto-organizzarsi.
Uno degli approcci modellistici più in voga nella letteratura scientifica è quello macroscopico, così chiamato perché adotta un punto di vista a larga scala e guarda alla densità dei pedoni, assimilando idealmente questi ultimi ad un mezzo continuo (ad esempio un fluido) distribuito nello spazio. Il principio di base dei modelli macroscopici è la conservazione della massa: durante il moto i pedoni si spostano da un luogo all'altro, ma la loro quantità totale non varia almeno finché essi non escono dalla zona di osservazione. Ciò significa che la variazione nel tempo della quantità di pedoni in una qualsiasi sotto-zona, diciamo S, è dovuta unicamente al flusso di pedoni che ne attraversano il contorno:
variazione dei pedoni contenuti in S = (flusso entrante in S) - (flusso uscente da S).
I modelli considerano inoltre che la dinamica del sistema è determinata essenzialmente da due fattori: da un lato la volontà di ogni pedone di raggiungere una certa destinazione, dall'altro le interazioni che possono far deviare i pedoni dalle loro traiettorie preferenziali (infatti le persone generalmente non amano stare troppo a contatto e tendono ad evitare le zone di maggiore affollamento). Risolvendo le equazioni dei modelli con un computer si può visualizzare la densità dei pedoni a diversi istanti di tempo e trarre indicazioni utili sul raggiungimento di particolari livelli critici di congestione in alcune aree.
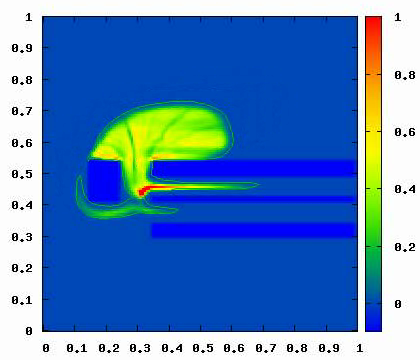
Simulazione di flusso pedonale
attraverso passaggi stretti
Un modello matematico per la simulazione dei flussi pedonali mette a disposizione un "laboratorio virtuale" per studiare, in tempi relativamente brevi e a costo quasi nullo, molte situazioni spesso non facilmente sperimentabili in pratica. Infatti, non è semplice realizzare esperimenti per raccogliere dati sul comportamento dei pedoni, perché le persone possono essere influenzate dal fatto di sapersi osservate o dal fatto di sapere che stanno effettuando una simulazione. Inoltre, i dati sperimentali non costituiscono da soli strumenti di indagine sufficienti, poiché sono istantanee statiche di eventi particolari, mentre i fenomeni più interessanti avvengono a livello dinamico e sono diversi caso per caso (Si veda qui a fianco una simulazione bidimensionale di un flusso di pedoni attraverso passaggi stretti. I colori rappresentano i diversi valori assunti dalla densità della folla nei punti del piano, in base alla scala mostrata sulla destra). I modelli matematici colgono invece il caso medio, ne descrivono l'evoluzione dinamica e permettono di riprodurlo un numero illimitato di volte.



