Roberto Battiston propone un metodo per lo studio dell'andamento dell'epidemia da Covid-19 nelle province italiane.
La recente polemica sull’affidabilità del dato tramesso all’Istituto Superiore di Sanità da parte della regione Lombardia, dato utilizzato dalla Fondazione Bruno Kessler per calcolare l’indice $R(t)$, solleva la questione molto importante sulla qualità dei dati a disposizione per analizzare l’andamento dell’epidemia COVID-19. Non è certamente la prima volta che si parla di questo tema, sollevato da molti esperti fin dal periodo della prima ondata e del lockdown di marzo: a un anno dall’inizio dell’epidemia ci troviamo però ancora con una situazione insoddisfacente e che richiede chiarimenti ed interventi risolutivi. Il dato epidemico, infatti, determina molte scelte relativamente alle politiche di contenimento, scelte che hanno impatti rilevantissimi sulla società, con aspetti che vanno da quelli sanitari a quelli economici.
Ricordiamo che la raccolta e il trasferimento dei dati avviene attraverso due percorsi diversi che partono dalla periferia e arrivano a Roma. Il primo percorso riguarda i dati raccolti nel sito pubblico, https://github.com/pcm-dpc/COVID-19, mantenuto dalla Protezione Civile1. Si tratta di un lavoro di raccolta prezioso e quotidiano, su cui si basa l’informazione giornaliera a disposizione di chi analizza il dato epidemico, dai ricercatori ai media. Allo stesso tempo si tratta di un dato non certificato: con una certa frequenza si osservano aggiornamenti, ritardi nelle comunicazioni, variazioni quotidiane che non sono compatibili con l’andamento epidemico - ad esempio improvvisi salti nei dati, a salire ma anche a scendere - che ovviamente introducono delle incertezze nell’analisi. Per questi motivi, nel gergo di chi analizza i dati, spesso questi dati sono chiamati "sporchi". In alcuni casi le conclusioni che se ne traggono possono essere messe in discussione perché potrebbero essere influenzate da errori significativi. Il secondo percorso riguarda i dati raccolti direttamente dall’Istituto Superiore di Sanità (ISS). Si tratta di dati molto più dettagliati, in cui vi sono informazioni sulla data dei primi sintomi e altre informazioni legate al singolo paziente: per questo motivo questi dati non sono resi pubblici anche se è in corso una condivisione con l’Accademia dei Lincei, a seguito di un accordo tra le due istituzioni.
In questo articolo mi limito a discutere dei dati raccolti dalla Protezione Civile, con l’obiettivo di mettere in evidenza alcune criticità ma anche di proporre delle soluzioni che ne permettano un migliore utilizzo, in particolare analizzando il dato provinciale.
Nella Figura 1, viene mostrato l’andamento nel tempo degli infetti attivi, $I(t)$, per la Toscana. Si identificano facilmente i picchi della prima e della seconda ondata (punti arancioni) e l’andamento di $R^*(t)$, il parametro di diffusione, calcolato secondo il metodo riportato qui (linea blu).

Figura 1
Nella Figura 2, la stessa quantità è mostrata per il Trentino. Si vede subito che vi sono importanti discontinuità nella curva $I(t)$, sia nella prima fase che che durante la seconda. Siccome $R^*(t)$ è strettamente collegato alla derivata logaritmica nel tempo di $I(t)$, $dln\left(I(t)\right)/dt$, a ognuna di queste discontinuità è associata una grande oscillazione di $R^*(t)$, anch’essa non imputabile ovviamente all’epidemia. Nel corso della seconda ondata, l’andamento di $I(t)$ diventa completamente caotico, come se venissero cambiate frequentemente le definizioni di infetto o di guarito. La stessa situazione si osserva in modo più o meno marcato per quattro altre regioni: Alto Adige, Marche e Molise e Veneto (Figure 3-6).

Figura 2

Figura 3

Figura 4

Figura 5

Figura 6
Fenomeni molto meno accentuati si osservano anche in altri casi, come la Lombardia (Figura 7) dove, oltre un salto a scendere ai primi di dicembre, si osserva un andamento "a gradini" nella coda finale.

Figura 7
Per ovviare a questa situazione è stata sviluppata l’analisi descritta nel seguito, che parte dall’andamento del numero totale di casi, $C(t)$, per derivare l’andamento di $I(t)$, sfruttando le equazioni del modello compartimentale SIR. $C(t)$ è una funzione monotona del tempo, che cresce a mano a mano che i casi vengono registrati. Non tiene conto di guarigioni e decessi e quindi è meno sensibile a cambiamenti di definizione o di trattamento della malattia. Non è immune a tutte le possibili distorsioni indotte sui dati da un inserimento non uniforme delle informazioni, come ad esempio nel caso in cui un infetto non entra mai nel conto dei casi, ma l’uso di C(t) riduce certamente l’effetto delle fluttuazioni improvvise non collegabili all’andamento epidemico.
Per il modello SIR valgono le seguenti relazioni:
\begin{equation} \begin{cases} &C(t) = I(t) + RIS(t)\\ &\frac{d\,RIS(t)}{dt} = \gamma\,I(t) \rightarrow RIS(t) = \gamma\int I(t) dt \end{cases} \end{equation}
dove $RIS(t)$ è il numero dei Risolti = Morti + Guariti.
Se discretizziamo la variabile tempo nelle equazioni precedenti, otteniamo:
\begin{equation}C(1) = I(1) + \gamma I(1) = (1 +\gamma) I(1) \rightarrow I(1) = \frac{C(1)}{1+\gamma}\end{equation}
\begin{equation}C(2) = I(2) + \gamma \left[I(1) + I(2)\right] = (1 +\gamma) I(2) + \gamma I(1) \rightarrow I(2) = \frac{C(2)}{1+\gamma} -\frac{\gamma}{1+\gamma} I(1)\end{equation}
Iterativamente otteniamo:
\begin{equation}I^{*}(n) = \frac{C(n)}{1+\gamma} -\frac{\gamma}{1+\gamma} \sum_{i=1,\ldots,n-1}I^{*}(i)\end{equation}
dove abbiamo utilizzato l’asterisco $I^{*}(t)$ per identificare la nuova funzione che descrive l’andamento degli infetti attivi nel tempo ricavata dal numero totale di infezioni $C(t)$. Il parametro $\gamma$ è il tasso di guarigione, in unità 1/giorni: risulta diverso per le diverse regioni e per il caso nazionale, ed è usato in questo metodo per calibrare la forma di $I^{*}(t)$ in modo da farla corrispondere a quella osservata $I(t)$.
Nelle figure seguenti vengono riportate le due funzioni $I(t)$ e $I^{*}(t)$ per il caso nazionale e per le ventuno regioni.
Nella Figura 8 riportiamo il caso per l’Italia: in rosso il dato $I(t)$, in blu la funzione $I^{*}(t)$, con $\gamma=0.11=1/9$ giorni. Osserviamo un ottimo accordo, ma la curva blu, $I^{*}(t)$, è leggermente più regolare di quella rossa, $I(t)$: in altri termini la curva blu segue più da vicino un andamento SIR, probabilmente correggendo anomalie presenti nel reporting quotidiano non imputabili all’epidemia.

Figura 8
Nella Figura 9 riportiamo il caso per le ventuno regioni italiane: anche in questo caso in rosso il dato $I(t)$, il numero di infetti attivi secondo i dati della Protezione Civile, in blu la funzione $I^{*}(t)$, quella calcolata a partire dal numero totale di infezioni $C(t)$: $\gamma$ è stato scelto in ogni regione in modo da fare corrispondere nel modo migliore la curva rossa con quella blu. Osserviamo un ottimo accordo per alcune regioni, un accordo buono per altre. Ve ne sono sei per cui l’accordo non è buono: Basilicata, Alto Adige, Trentino, Marche, Molise e Veneto. Per le ultime cinque (Alto Adige, Trentino, Marche, Molise e Veneto) si tratta delle regioni per le quali l’andamento di $I(t)$ non è compatibile con uno sviluppo epidemico. La funzione $I^{*}(t)$ per queste cinque regioni è quindi preferibile, in quanto maggiormente compatibile con una descrizione epidemica di tipo SIR.

Figura 9
Le stesse considerazioni possono essere fatte per le province, dove non è disponibile il dato $I(t)$ ma solo il dato $C(t)$. In questo caso il confronto può essere fatto fra la quantità $I^{*}(t)$ e la quantità $I(t)$ (o $I^{*}(t)$ per le cinque regioni di cui sopra, tranne che per Trentino e Alto Adige per cui il dato regionale coincide con quello provinciale) per la corrispondente regione. Tutti i grafici sono normalizzati al punto di massimo delle curve.
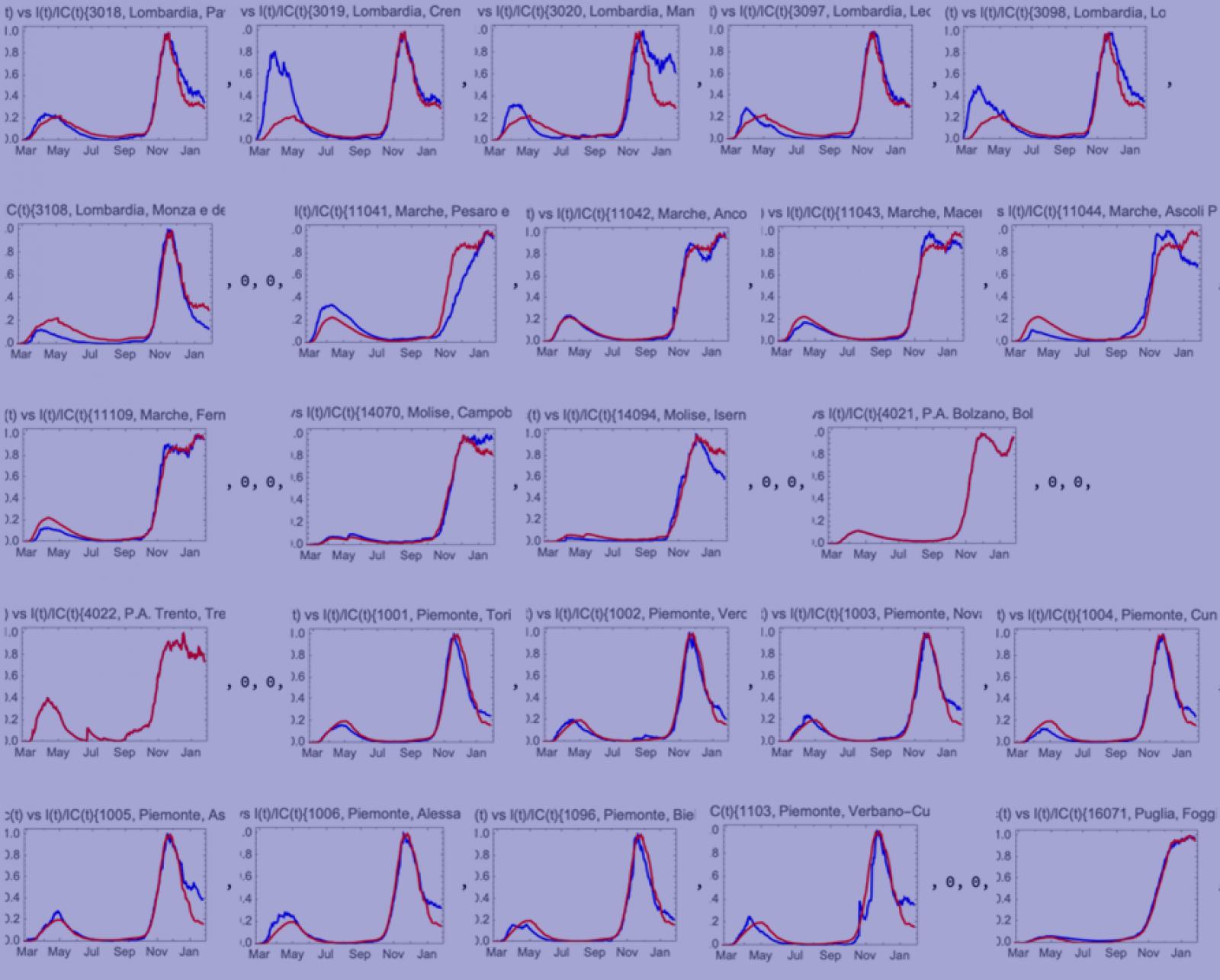
La figura 10 mostra il risultato per le ventuno regioni confrontate con le corrispondenti 107 province. Le differenze che si notano tra i vari $I^{*}(t)$ provinciali e quello della corrispondente regione sono dovute a due tipi di effetti:
- variabilità dell’andamento epidemico tra provincia e provincia,
- eventuali limiti del metodo impiegato che non vengono rivelati dall’analisi a livello regionale: per tutte le province viene usato lo stesso fattore $\gamma$, fattore che è collegato alla risposta del sistema sanitario all’epidemia. Se questo fattore varia da provincia a provincia e non segue uno standard regionale, questo fatto si ripercuoterebbe sulla forma delle curve $I^*(t)$ a livello provinciale.
Da un punto di vista metodologico, è stato verificato che, data una stessa regione, il parametro $\gamma$ non dipende dal tempo o dalle fasi dell’epidemia. In assenza di altre informazioni, nel seguito si assume quindi che l’effetto principale sia dovuto al punto 1. e che quindi le differenze osservate tra le diverse province, rispetto all’andamento regionale, siano attribuibili al reale andamento epidemico a livello locale. A titolo di esempio si prende il caso delle province della Lombardia: risulta evidente la differenza nella prima ondata, dove le province di Bergamo, Brescia e Lodi risultano maggiormente colpite. Interessante è anche l’andamento delle province dell’Emilia-Romagna, dove la prima ondata appare molto più intensa della media regionale per le province contigue alla Lombardia, mentre la seconda ondata appare più intensa della media regionale per le province adiacenti al Veneto. Relativamente al Veneto, dove viene fatto il confronto con l’$I^{*}(t)$ regionale per le ragioni riportate sopra, si osserva un andamento molto uniforme di tutte le province rispetto all’andamento regionale, sia per la prima che per la seconda ondata. Infine, per le province di Trento e di Bolzano, la curva $I^{*}(t)$ rappresenta, secondo questa analisi, il «vero» andamento dell’epidemia nelle due province, da utilizzare al posto della curva $I(t)$ ricavata direttamente dal dato della Protezione Civile. Esistono molti altri effetti a livello provinciale, che con questo metodo sono messi in evidenza e possono essere oggetto di analisi.






Figura 10
Il dato provinciale così ottenuto può essere analizzato nelle modalità con cui fino ad ora è stato analizzato il dato regionale. Nel seguito sono riportati alcuni esempi (Figure 11 e 12).
Per la lista completa ci si può riferire al sito www.robertobattiston.it.

Figura 11

Figura 12


