Analisi dei dati epidemiologici del coronavirus in Italia: nota metodologica
- 48609 letture

I dati qui analizzati sono stati scaricati dal repository della Protezione civile. Tra i vari modelli matematici a disposizione per descrivere il fenomeno della diffusione dell’epidemia del coronavirus, uno dei più semplici coinvolge alcuni “compartimenti”. Il primo compartimento S contiene gli individui che non presentano il virus all’interno del loro corpo e che risultano quindi “suscettibili” di essere infettati. Da questo compartimento ciascun individuo può spostarsi nel secondo compartimento I dove ci sono invece gli individui che sono stati infettati. Da qui ciascun individuo può andare in un terzo compartimento M che contiene i soggetti che hanno sviluppato i sintomi della malattia, diagnosticata di conseguenza tramite test e che siano stati isolati, a casa, in ospedale o in terapia intensiva. Da questo compartimento, un individuo passerà nel quarto e ultimo compartimento R dove si trovano gli individui guariti e quelli morti. Assumiamo qui che i guariti non contengano più il virus, o che comunque non possano trasmetterlo ad altri individui infettandoli. È comunque stato riportato che in Cina circa il 14% dei pazienti guariti dall’infezione da coronavirus presentano il virus nelle feci dopo due settimane dalla dimissione. Osserviamo che non tutti gli individui infetti passano nel compartimento M. Questo può accadere sia per una mancata o erronea diagnosi e/o isolamento. Più preoccupante è il caso in cui una frazione non trascurabile degli infetti non sviluppino i sintomi della malattia, pur potendo trasmetterla, cioè siano “portatori sani”. Questo sembra essere il caso per il coronavirus. Purtroppo, da circa la fine di febbraio non vengono più effettuati test diagnostici a campione sugli asintomatici che permetterebbero una stima della frazione dei portatori sani.
Consideriamo le quattro funzioni S(t), I(t), M (t) e R(t) che descrivono il numero di individui presenti al tempo t in ciascuno dei quattro compartimenti. A questo punto possiamo ragionare in termini deterministici considerando il flusso di spostamento da S ad I, quello da I ad M e quello da M ad R. Il primo flusso può essere assunto proporzionale sia al numero di individui suscettibili S(t) che al numero di infetti I(t). Gli altri due flussi possono invece essere assunti proporzionali ad I(t) e ad M(t) rispettivamente. Analogamente, possiamo ragionare in modo probabilistico rimpiazzando i flussi con delle probabilità. Nel caso deterministico, le tre funzioni possono essere determinate risolvendo numericamente un sistema di equazioni differenziali ordinario. Nel caso stocastico possiamo usare invece l’algoritmo di simulazione di Gillespie.
Ci siamo finora focalizzati sul numero C(t) = M (t) + R(t) di persone che sono state contagiate ed osservate fino al tempo t. Abbiamo optato per questa scelta sperando che gli errori da cui sono affette le misure delle singole variabili, e.g. il numero dei morti, di cui C(t) è la somma, si compensino. La funzione C(t) è per definizione crescente nel tempo, o meglio non decrescente. Inoltre, dalle soluzioni ottenute numericamente, osserviamo un aumento progressivo del tasso di crescita di C(t) fino ad un massimo oltre il quale tale tasso diminuisce, mentre C(t) continua a crescere ma sempre più lentamente e dopo un tempo sufficientemente lungo non ha in pratica più variazioni. Una funzione che ha questo andamento è la funzione “logistica”
y 0 /(1 + exp(−(t − t 0 )/τ ))
come mostrato in figura 1. Dei tre parametri y 0 , t 0 e τ contenuti in questo modello, il parametro positivo τ influenza la velocità con cui viene raggiunto il valore limite: diminuendo il suo valore, aumenta tale velocità.

Figura 1. Esempio di andamento temporale di una variabile descritta da una funzione logistica.
In figura 2 si osserva la sequenza temporale della frazione dei contagiati osservati in Italia rispetto alla popolazione nazionale, assieme ad un fit con due modelli matematici applicati in sequenza in ciascuno di due sotto-intervalli contigui in cui abbiamo diviso l’intervallo temporale. Il modello utilizzato in ciascun sotto-intervallo è di tipo geometrico y02t/τ . Questa funzione, al contrario della logistica, cresce indefinitivamente e cosı̀ fa anche il suo tasso di crescita. Il parametro positivo τ rappresenta il tempo di raddoppio del valore della funzione. Più basso è il valore di questo parametro, più rapidamente cresce nel tempo il valore della funzione. La scelta di usare due modelli in sequenza è stata motivata dal cambiamento del criterio di identificazione dei contagiati avvenuto alla fine del mese di Febbraio, che non coinvolge più l’uso di tamponi su soggetti asintomatici. Sfortunatamente, si intuisce facilmente che la frazione dei contagiati effettivi dopo il cambio di criterio risulta significativamente sottostimata. Sulla base dei dati osservati fino a 12 Marzo alle 18, a livello dell’intera Italia non c’è evidenza di riduzione del tasso di crescita dei contagiati osservati. Infatti l’adattamento del modello ai dati è equivalente a quello in cui la funzione geometrica nel secondo sotto-intervallo è sostituita dalla logistica.

Figura 2. Sequenza della frazione del numero dei contagiati osservati in Italia rispetto alla popolazione nazionale. Il miglior fit con un modello doppio geometrico è sovrapposto ai dati.
Abbiamo considerato le sequenze temporali dal 1 marzo della frequenza dei contagiati osservati rispetto alla popolazione regionale delle nove regioni più colpite del “nord”: Lombardia, Emilia, Veneto, Marche, Piemonte, Toscana, Liguria, Trentino e Friuli. Sulla base di questi dati, abbiamo raggruppato le nove regioni in tre gruppi ciascuno composto da sequenze “simili”. A questo scopo abbiamo utilizzato l’algoritmo di clustering gerarchico che minimizza localmente la somma delle variazioni dei dati all’interno di ciascun gruppo. Nella Figura 3 viene mostrato il cosiddetto “dendrogramma”, cioè l’albero che visualizza i successivi raggruppamenti dell’algoritmo. Si parte dal livello più basso, dove ciascuna delle nove sequenze costituisce un gruppo sino ad arrivare al livello più alto, dove tutte e nove le sequenze sono in un unico gruppo. Il dendrogramma mostra chiara evidenza della presenza di tre gruppi:
- Lombardia;
- Emilia, Veneto e Marche;
- Piemonte, Toscana, Liguria, Trentino e Friuli.
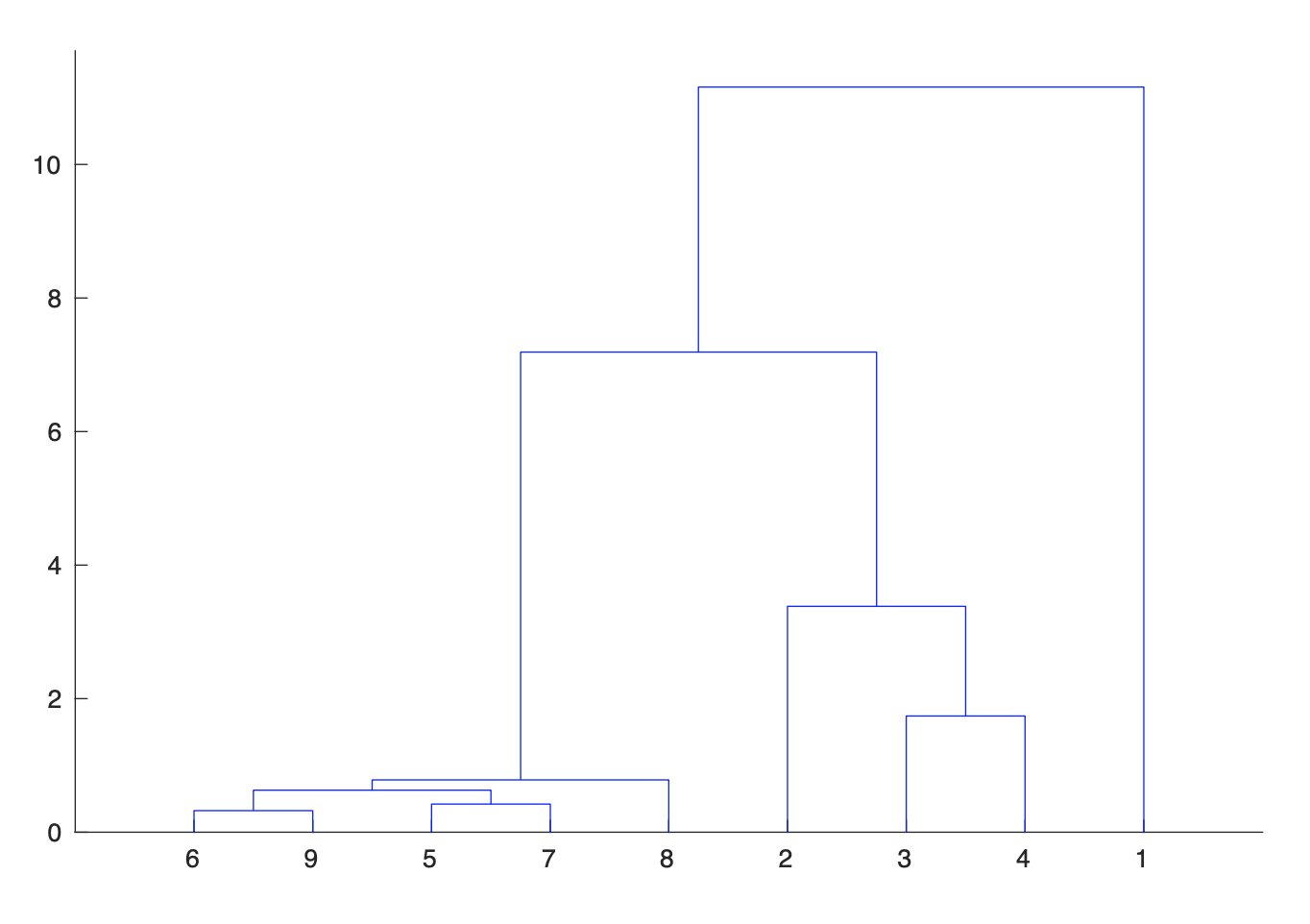
Figura 3. Dendrogramma per il raggruppamento delle nove regioni considerate tramite l’algoritmo di clustering gerarchico applicato alle nove sequenze delle frazioni dei contagiati osservati a partire dal 1 Marzo.
Per la Lombardia non si osserva evidenza di diminuzione del tasso di crescita della frazione dei contagiati osservati che segue un modello doppio esponenziale, come si può apprezzare in Figura 4 ed in Figura 5 a partire dal 1 marzo in scala semi-logaritmica, per cui la funzione esponenziale diventa una retta. Le sequenze relative alle regioni nel secondo gruppo mostrano evidenza di diminuzione del tasso di crescita. Infatti il modello logistico si adatta meglio ai dati di quello geometrico.
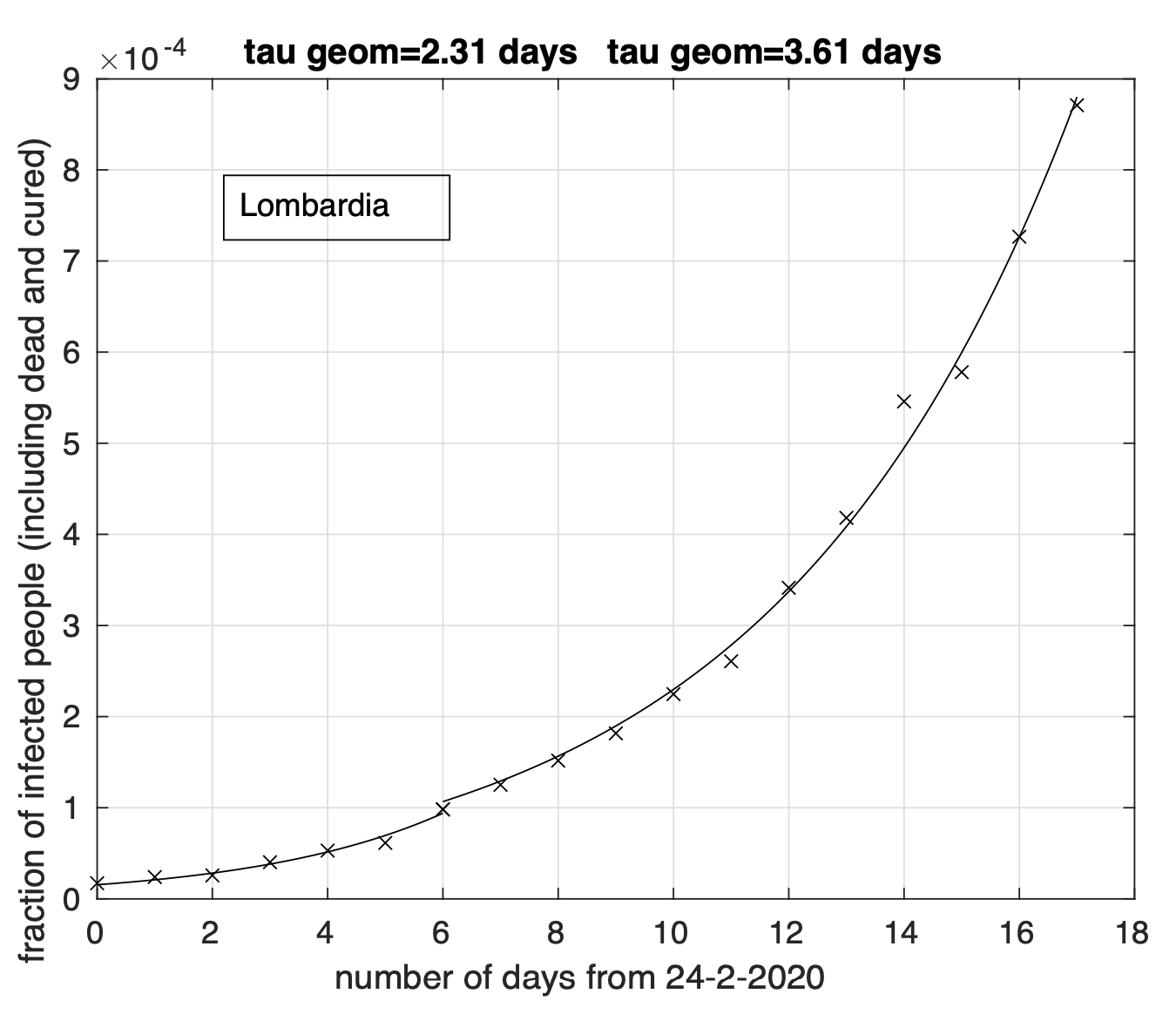
Figura 4. Sequenza della frazione dei contagiati osservati in Lombardia rispetto alla popolazione della regione. Il miglior fit con un modello doppio geometrico è sovrapposto ai dati.
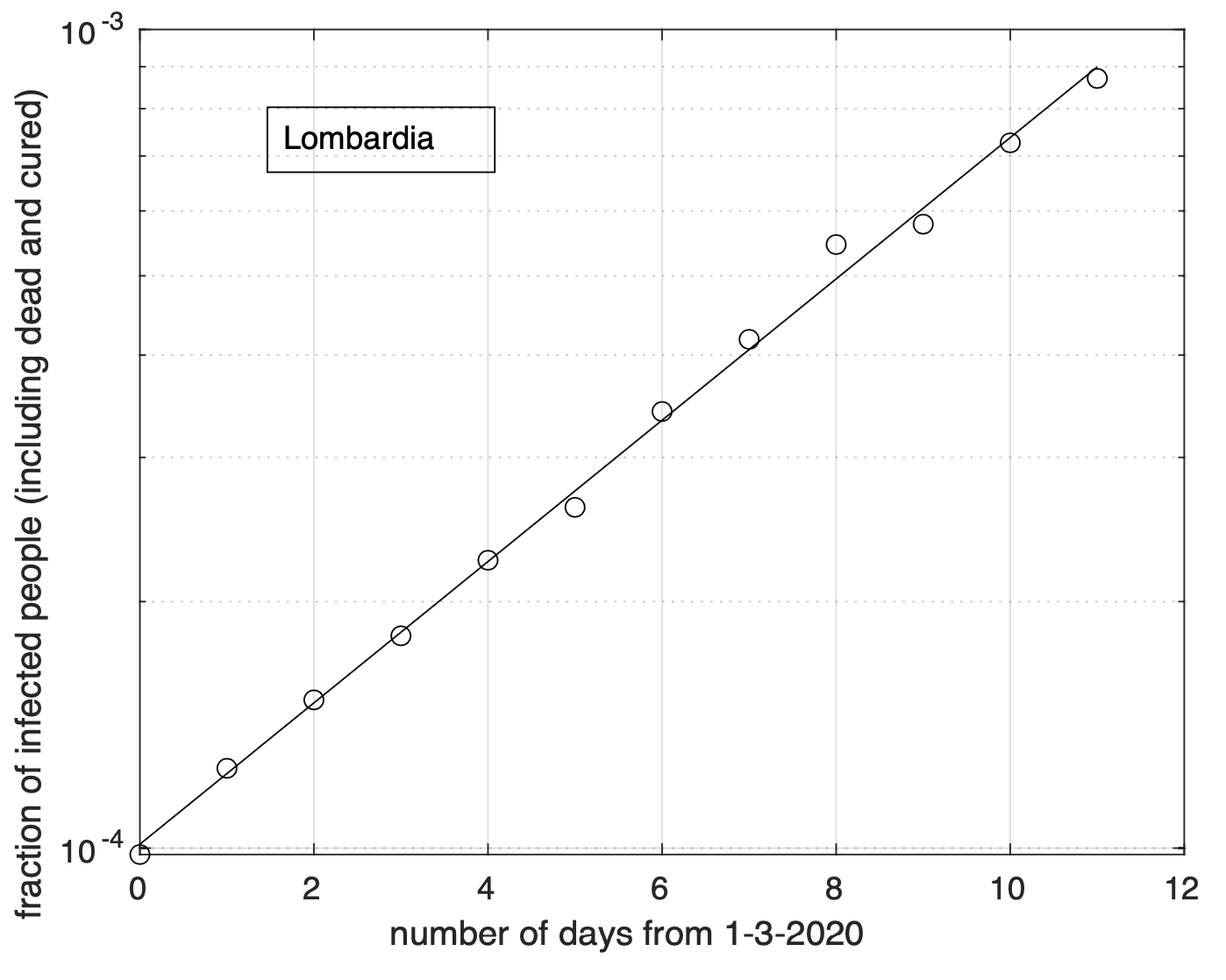
Figura 5. Come nella Figura 4, ma per i dati a partire dal 1 Marzo ed in scala semi-logaritmica. La linea retta rappresenta il modello esponenziale stimato a partire dai dati.
In Figura 6 possiamo osservare il risultato relativo all’Emilia. Questo è più evidente per le regioni del terzo gruppo, come ad esempio nel caso del Piemonte, illustrato in Figura 7.
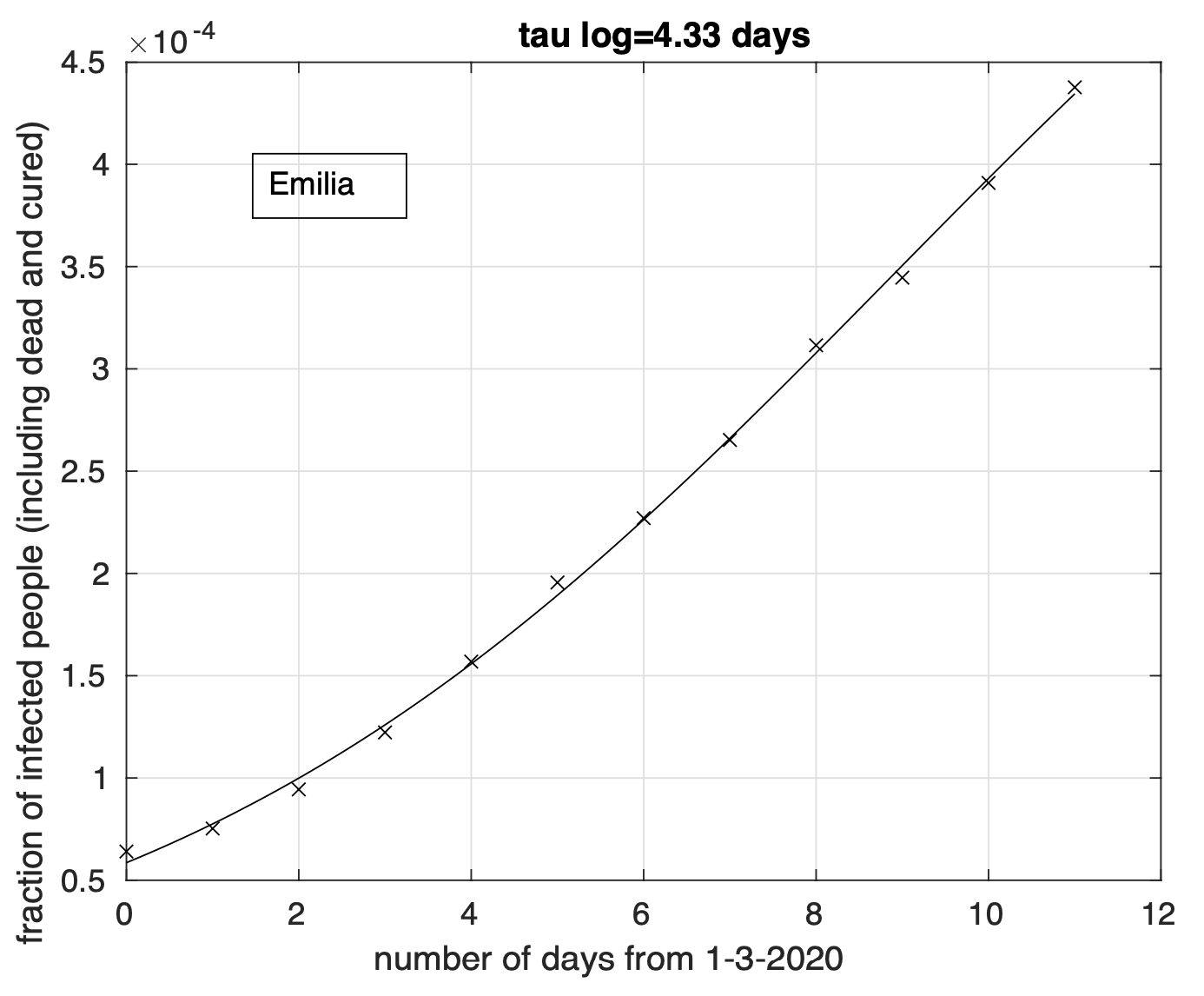
Figura 6. Sequenza della frazione dei contagiati osservati in Emilia rispetto alla popolazione della regione. Il miglior fit con un modello logistico è sovrapposto ai dati.
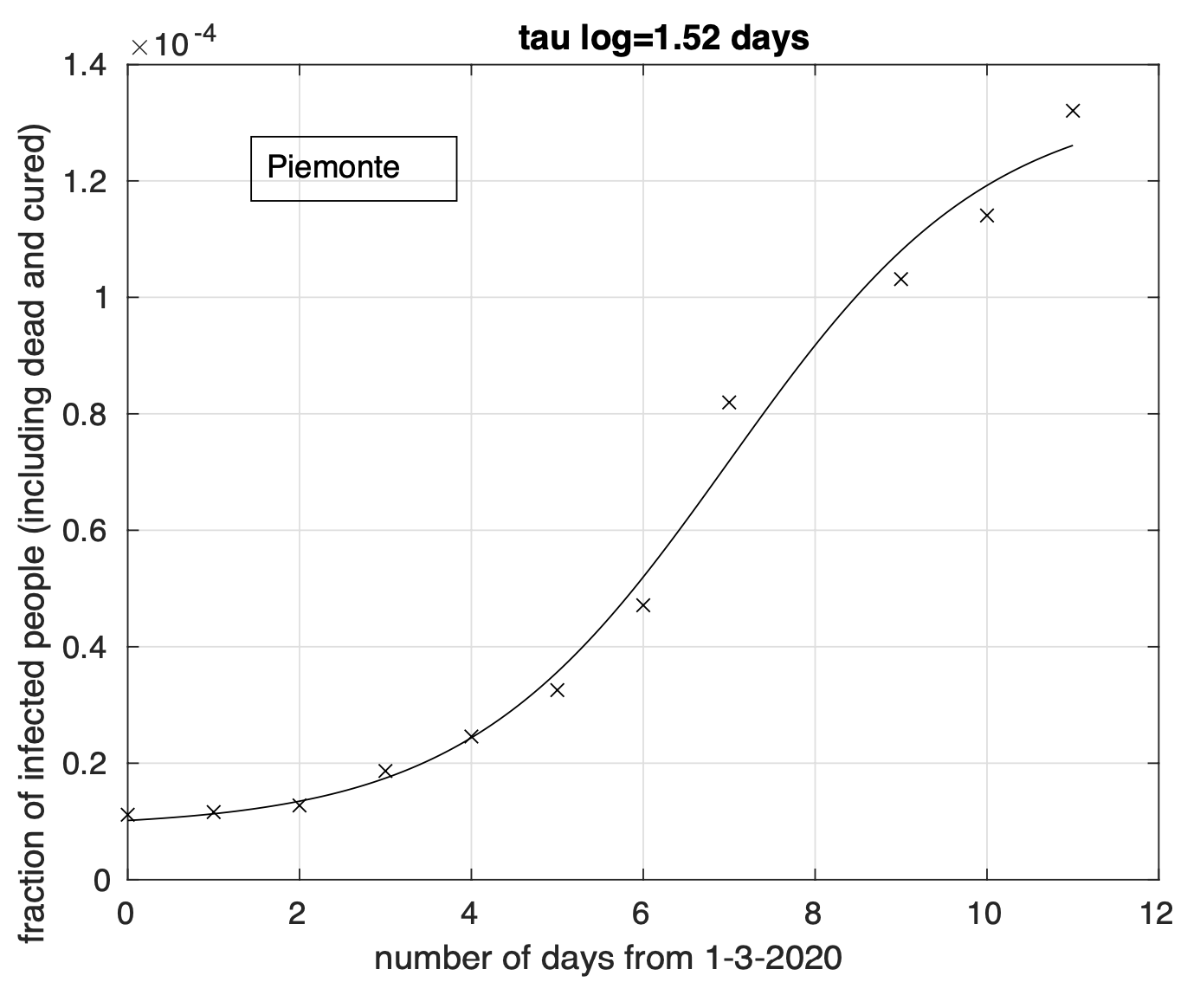
Figura 7. Sequenza della frazione dei contagiati osservati in Piemonte rispetto alla popolazione della regione. Il miglior fit con un modello misto geometrico-logistico è sovrapposto
ai dati.
I valori stimati del tempo dal 1 Marzo a partire dal quale non si avranno praticamente variazioni della frazione dei contagiati osservati sono stati stimati separatamente per ciascuna delle otto regioni rimaste dopo aver escluso la Lombardia. Sulla base del raggruppamento effettuato, riportiamo il range per il gruppo Emilia, Veneto e Marche: 40-60 giorni e quello per il gruppo Piemonte, Toscana, Liguria, Trentino e Friuli: 20-30 giorni. La bontà della stima dei range è limitata dal ridotto intervallo temporale in cui il tasso di crescita diminuisce. Col tempo tale intervallo aumentarà e di conseguenza anche la bontà della stima. Naturalmente questo vale se non ci saranno variazioni significative del comportamento della popolazione in relazione ai meccanismi principali alla base del fenomeno di diffusione del virus. Infatti, l’analisi effettuata oggi ha messo in evidenza un aumento del tasso di crescita a partire dal 10-11 Marzo che segue una sua precedente diminuzione per le sequenze di Sicilia (vedi Figura 8) e Lazio e meno marcatamente per la Puglia. È possibile che questo sia stato causato dall’esodo dal nord al sud avvenuto in seguito al decreto che l’8 marzo istituiva la zona rossa in Lombardia.
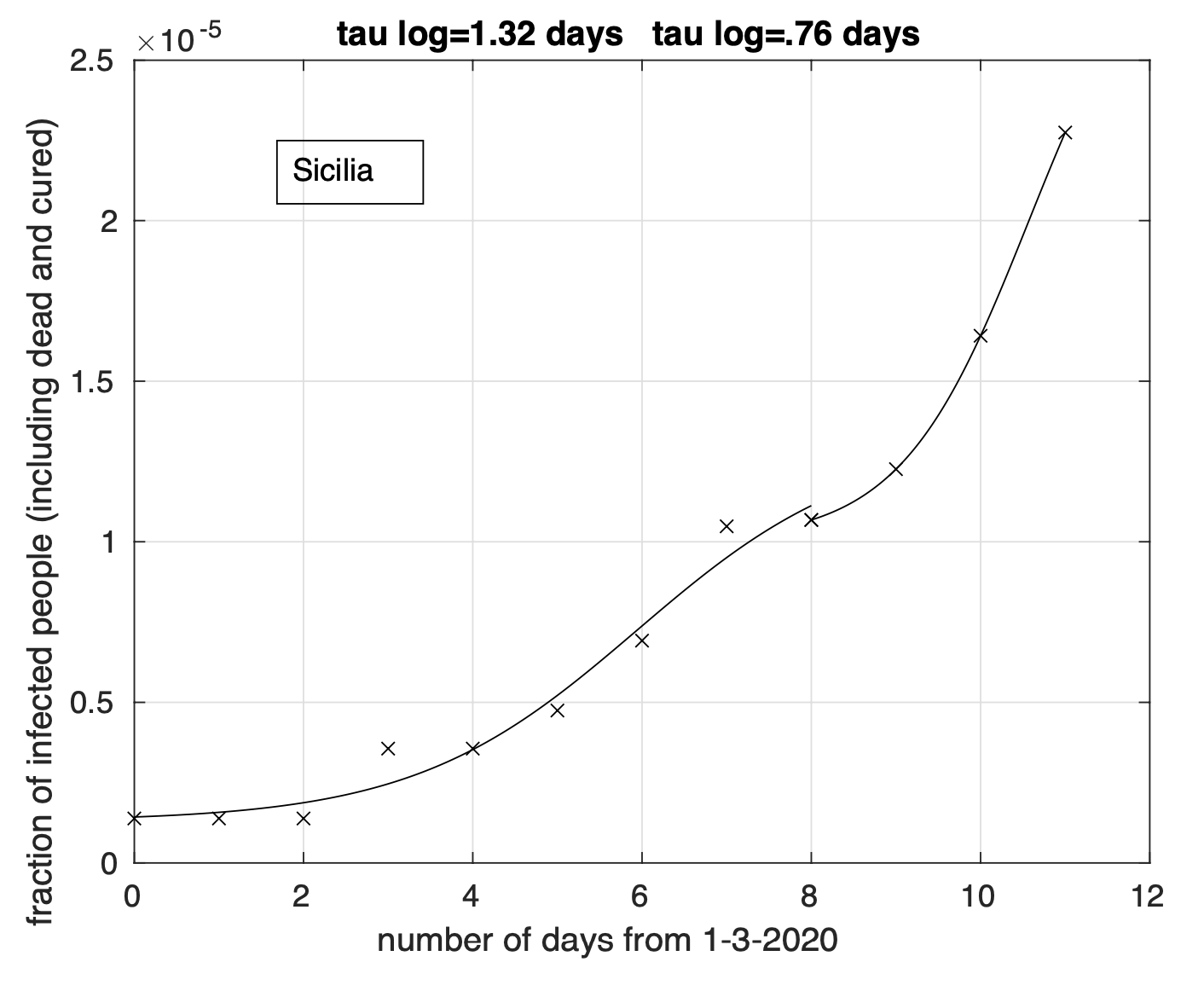
Figura 8. Sequenza della frazione dei contagiati osservati in Sicilia rispetto alla popolazione della regione. Il miglior fit con un modello doppio logistico è sovrapposto ai dati.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
Analisi dei dati epidemiologici del coronavirus in Italia (al 26 maggio)
- 6878 letture
Gli aggiornamenti successivi possono essere consultati questo link: https://www.scienzainrete.it/dashboard/
Oggi 26 maggio ci sono sei regioni dove l'aumento del numero totale di casi positivi rispetto a due settimane fa è inferiore a venti, le stesse che negli ultimi cinque giorni avevano lo stesso aumento massimo ma rispetto ai dieci giorni precedenti: la Calabria, la Basilicata, la Sardegna, la provincia di Bolzano, l'Umbria e la Valle D'Aosta. Le prime quattro, assieme al Molise, oggi hanno un valore nullo dell'incidenza.
La Sardegna sembra vicina alla fine dell'epidemia, seguita dall'Umbria e dalla Calabria.
Torna preoccupante la situazione nelle tre regioni più problematiche, la Lombardia, la Liguria, il Piemonte e nella provincia di Bolzano. Come previsto, la diminuzione dei valori di ieri dell'incidenza era principalmente dovuta al numero molto più basso di tamponi riportato, che prevediamo aumenti fino a venerdì.
Di seguito riportiamo i valori odierni dell’incidenza, ossia del numero di nuovi casi positivi al giorno per 100.000 abitanti.
Torna preoccupante la situazione per Lombardia, Liguria, Piemonte e la provincia di Trento, con valori dell'incidenza da 1,6 a 3,4 nuovi casi al giorno per 100.000 abitanti.
Situazione da monitorare con molta attenzione.
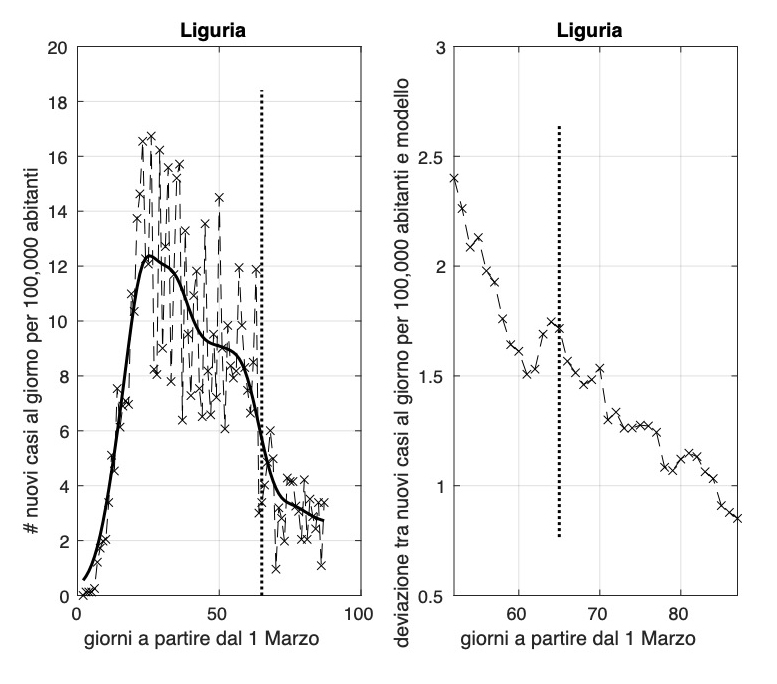
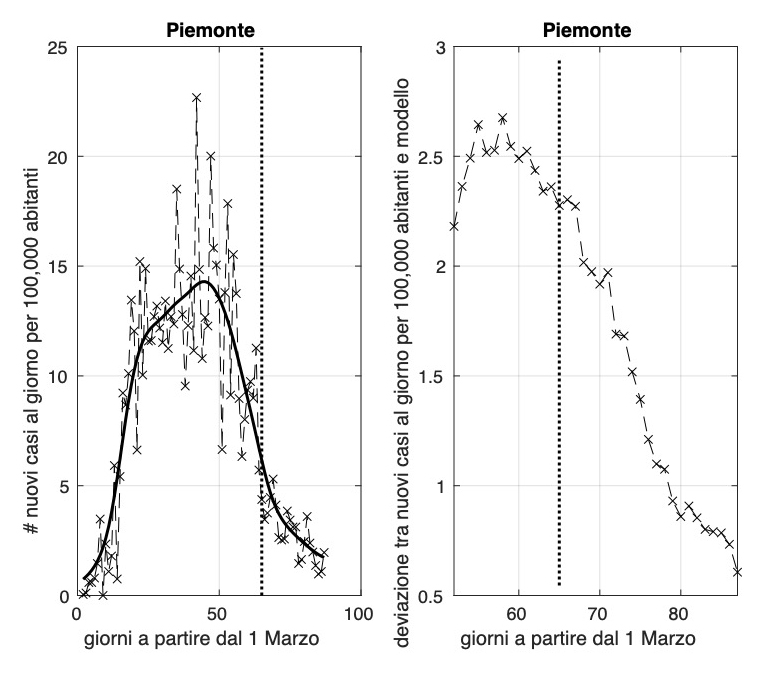
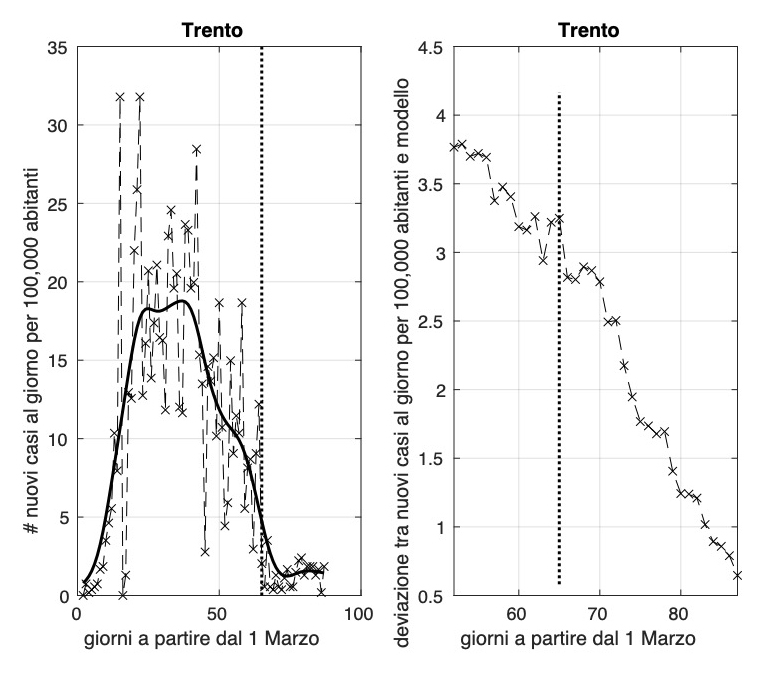
Ci sono tre regioni dove la diffusione dell'epidemia sembra essere terminata, prima fra esse, troviamo la Sardegna, seguita da Umbria e Calabria. Putroppo la Valle D'Aosta subisce un aumento dell'incidenza che arriva oggi ad un valore attorno a 1,6 nuovi casi al giorno per 100.000 abitanti.
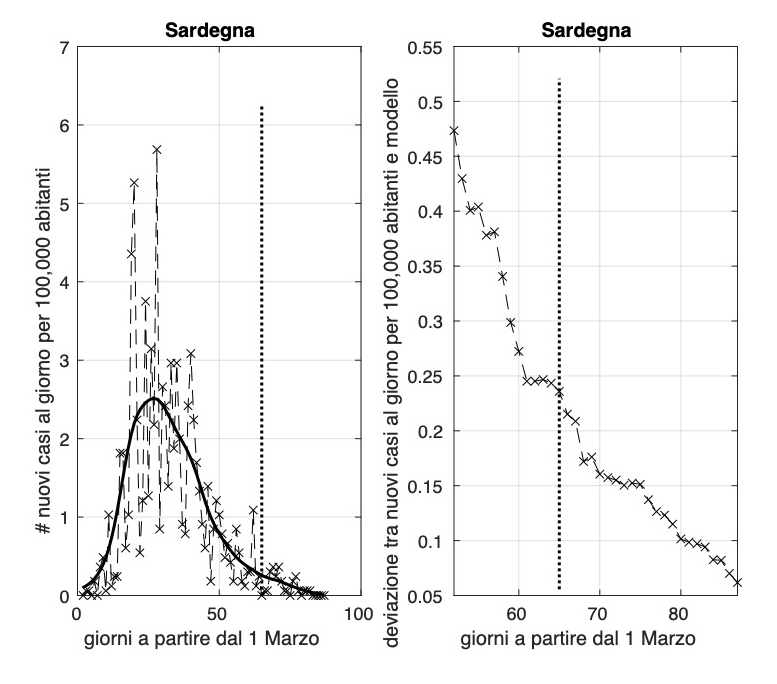
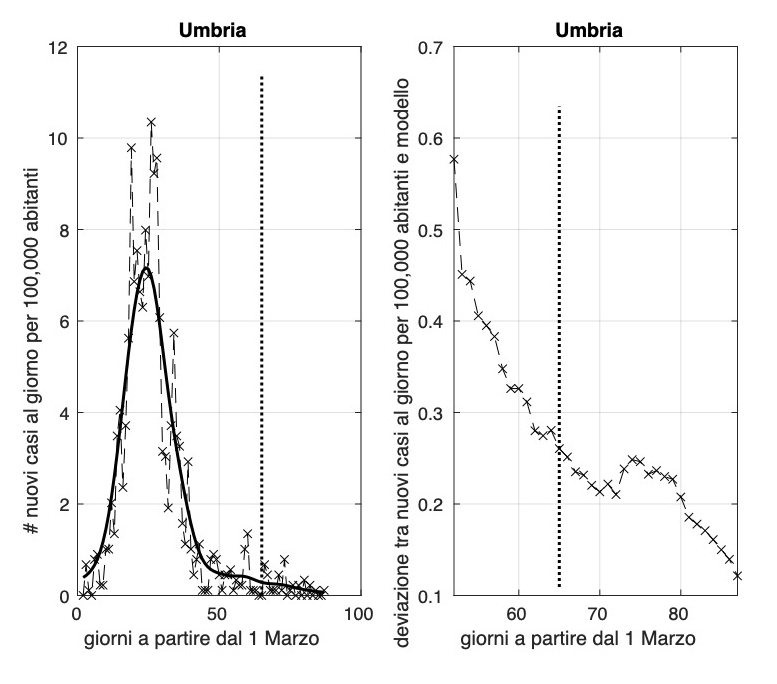
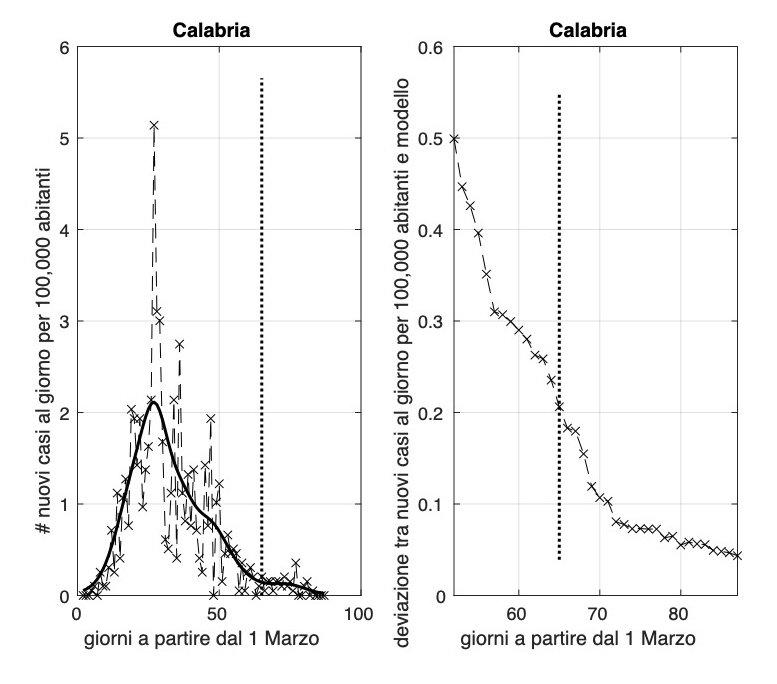
L'allarme per Puglia e Basilicata dovuto all'aumento significativo dell'incidenza degli ultimi tre giorni sembra rientrato, con un valore oggi quasi nullo per la Puglia e nullo per la Basilicata.
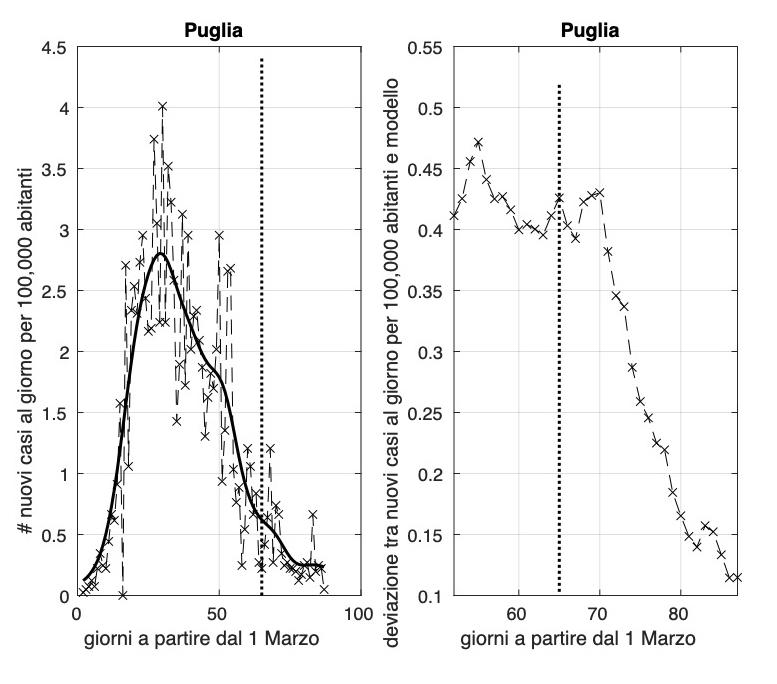

L'allarme per il Lazio sembra rientrato.
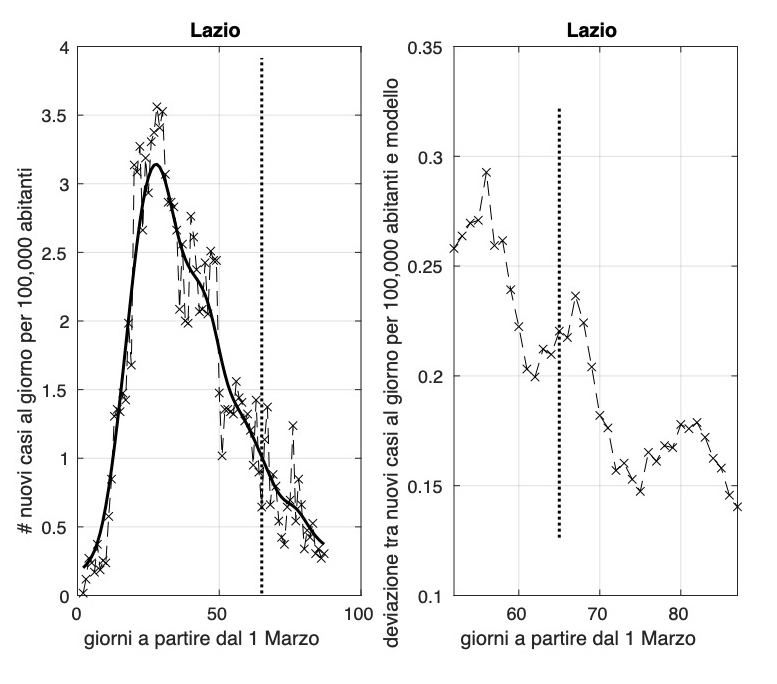 Lenta discesa dell'incidenza per regioni come la Campania, la Toscana ed il Friuli Venezia Giulia. Sembra rientrare l'allarme per le ultime due regioni dovuto all'aumento nei giorni scorsi. Utile osservare cosa accade nei prossimi giorni.
Lenta discesa dell'incidenza per regioni come la Campania, la Toscana ed il Friuli Venezia Giulia. Sembra rientrare l'allarme per le ultime due regioni dovuto all'aumento nei giorni scorsi. Utile osservare cosa accade nei prossimi giorni.
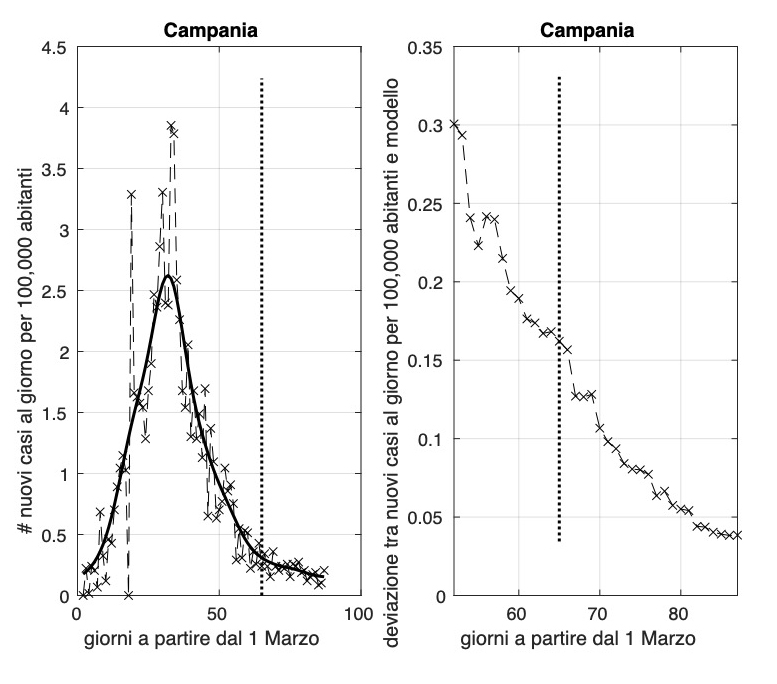
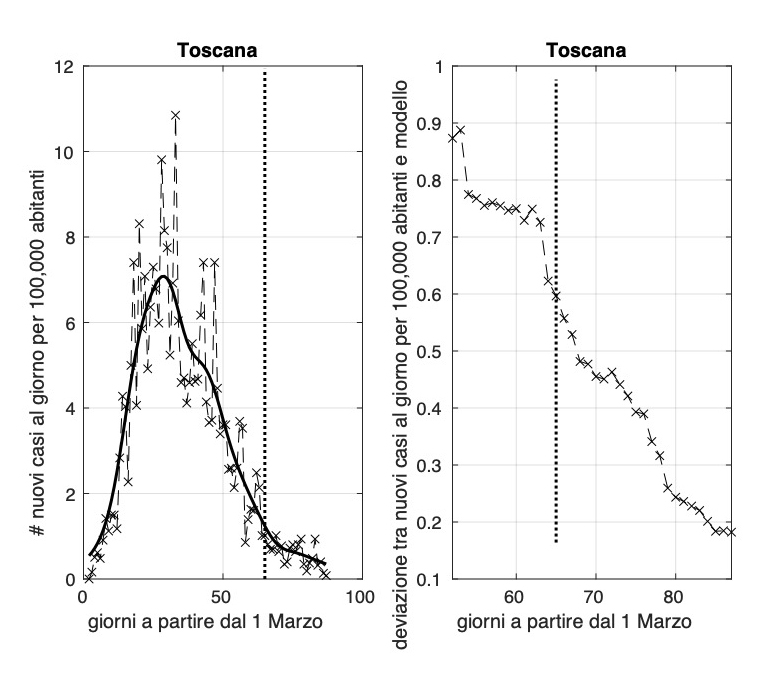
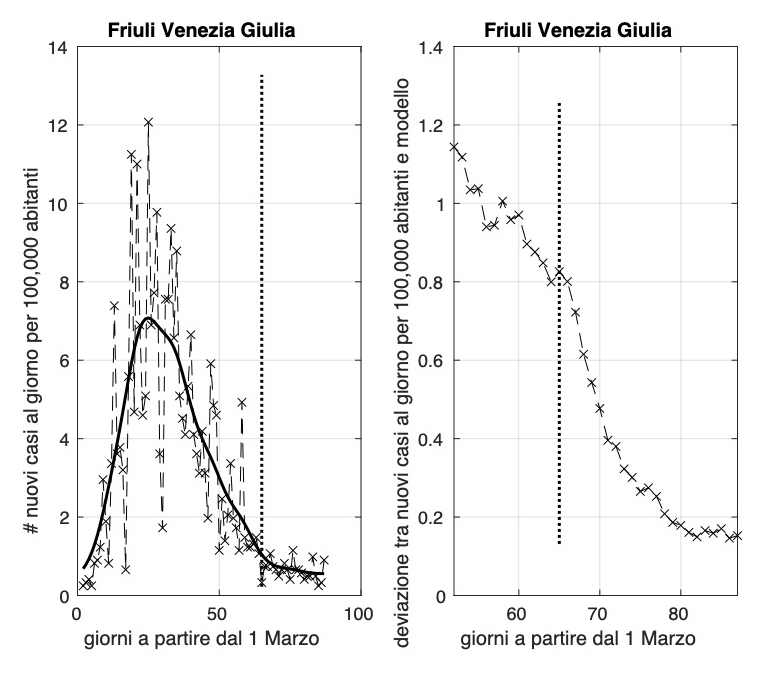
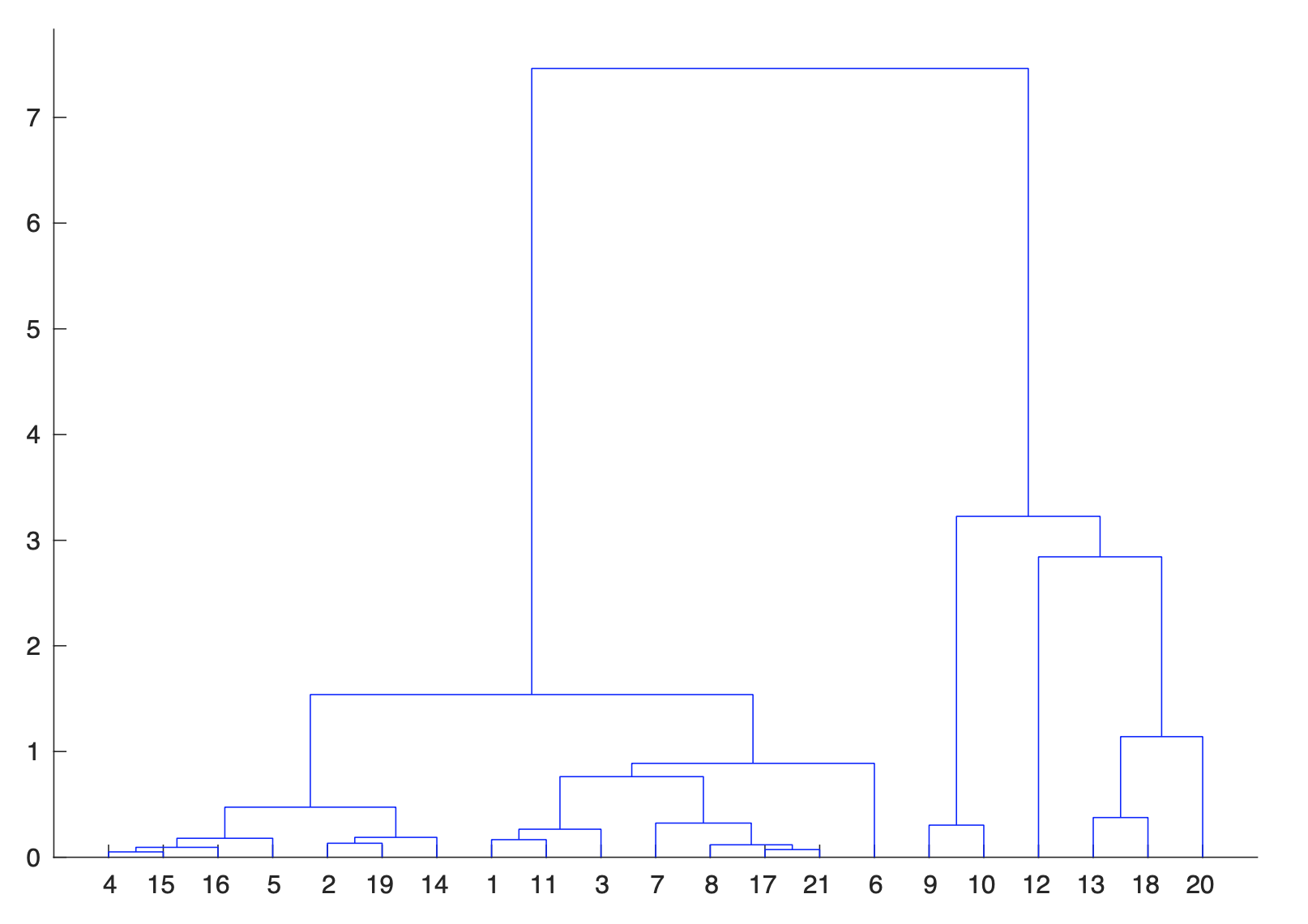
Dopo aver stimato per ciascuna regione il modello per l'andamento temporale dell'incidenza e calcolato la sua varianza, possiamo utilizzare i valori finali delle due quantità per formare dei "gruppi" di regioni con valori "vicini". Questo può essere fatto ad esempio con l'algoritmo del clustering gerarchico che minimizza localmente la somma delle varianze all'interno dei gruppi delle grandezze considerate. Nella figura seguente è illustrato tramite il "dendrogramma" il risultato ottenuto. Osserviamo l'evidenza di tre gruppi:
- Liguria, Lombardia, Molise, Piemonte, Trento e Valle D'Aosta dove i valori delle due grandezze sono grandi;
- Abruzzo, Bolzano, Emilia Romagna, Friuli Venezia Giulia, Lazio, Marche, Toscana e Veneto, con valori intermedi;
- Basilicata, Calabria, Campania, Puglia, Sicilia, Sardegna ed Umbria, con valori bassi.
Sembra definitivamente rientrato l'allarme per il Molise, dove ieri ed oggi l'incidenza è nulla. Anche la varianza continua a diminuire.
Osserveremo cosa succede nei prossimi giorni.
 La curva dell'incidenza "media" nelle regioni del secondo gruppo mostra che il valore limite al quale converge sembra maggiore di zero. E' come se ci fosse un livello di contagio che non si riesce ad eliminare.
La curva dell'incidenza "media" nelle regioni del secondo gruppo mostra che il valore limite al quale converge sembra maggiore di zero. E' come se ci fosse un livello di contagio che non si riesce ad eliminare.

Gli aggiornamenti successivi possono essere consultati questo link: https://www.scienzainrete.it/dashboard/
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
Analisi dei dati epidemiologici del coronavirus in Italia (al 25 maggio)
- 6010 letture
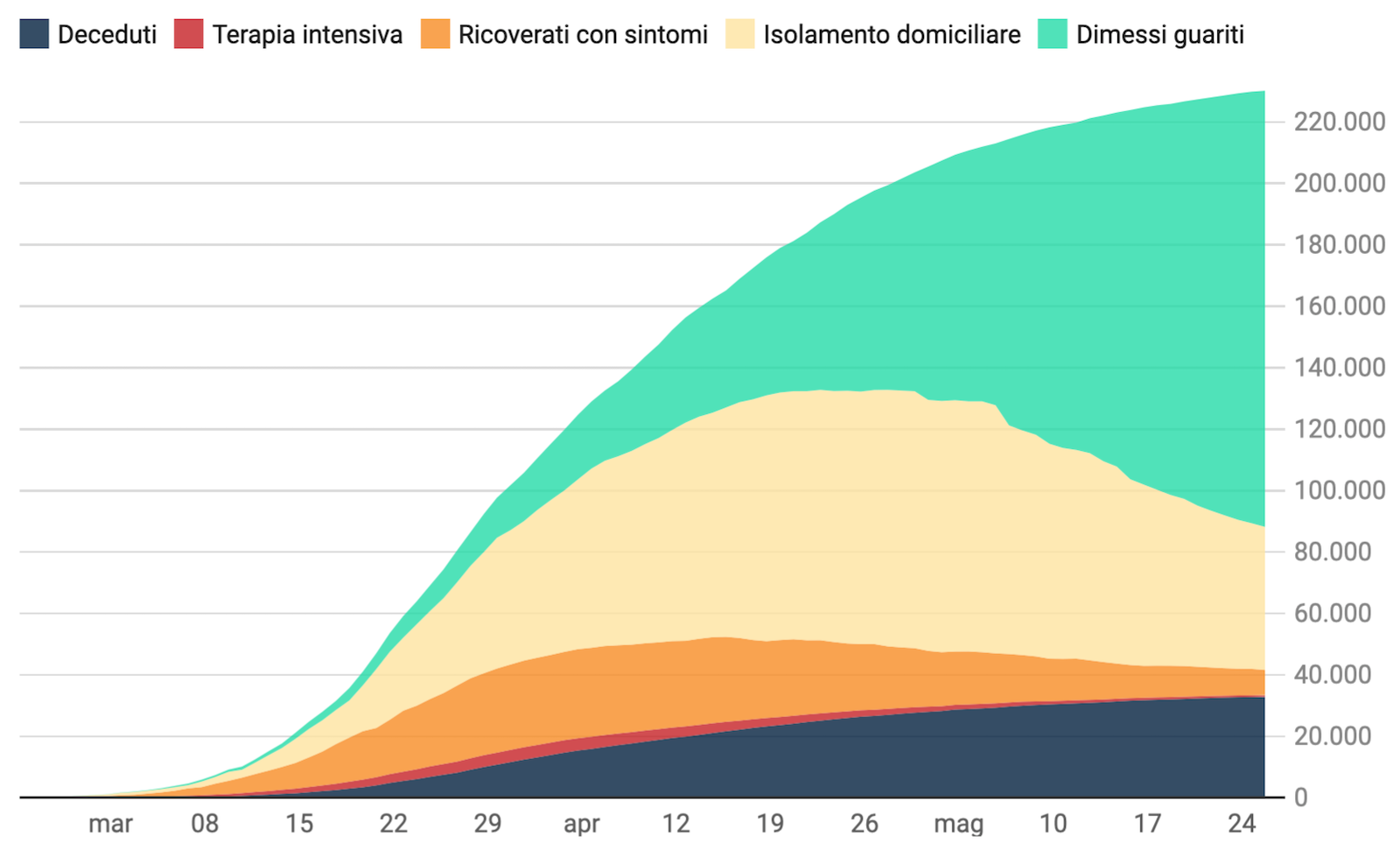
Oggi 25 maggio ci sono sei regioni dove l'aumento del numero totale di casi positivi rispetto a dieci giorni fa è inferiore a venti, le stesse degli ultimi quattro giorni: la Calabria, la Basilicata, l'Umbria, la provincia di Bolzano, la Sardegna e la Valle D'Aosta. Inoltre, per le prime quattro e il Molise oggi l'incidenza è nulla.
La Sardegna sembra vicina alla fine dell'epidemia, seguita dall'Umbria, dalla Calabria e dalla Valle D’Aosta.
Migliora la situazione nelle tre regioni più problematiche, la Lombardia, la Liguria, e la provincia di Trento, dove i valori oggi sono scesi in modo significativo. Ci aspettiamo che questa diminuzione sia largamente causata dal numero di tamponi oggi riportato, che il lunedì assume generalmente un minimo locale, come illustrato in figura.
Di seguito riportiamo i valori odierni dell’incidenza, ossia del numero di nuovi casi positivi al giorno per 100.000 abitanti
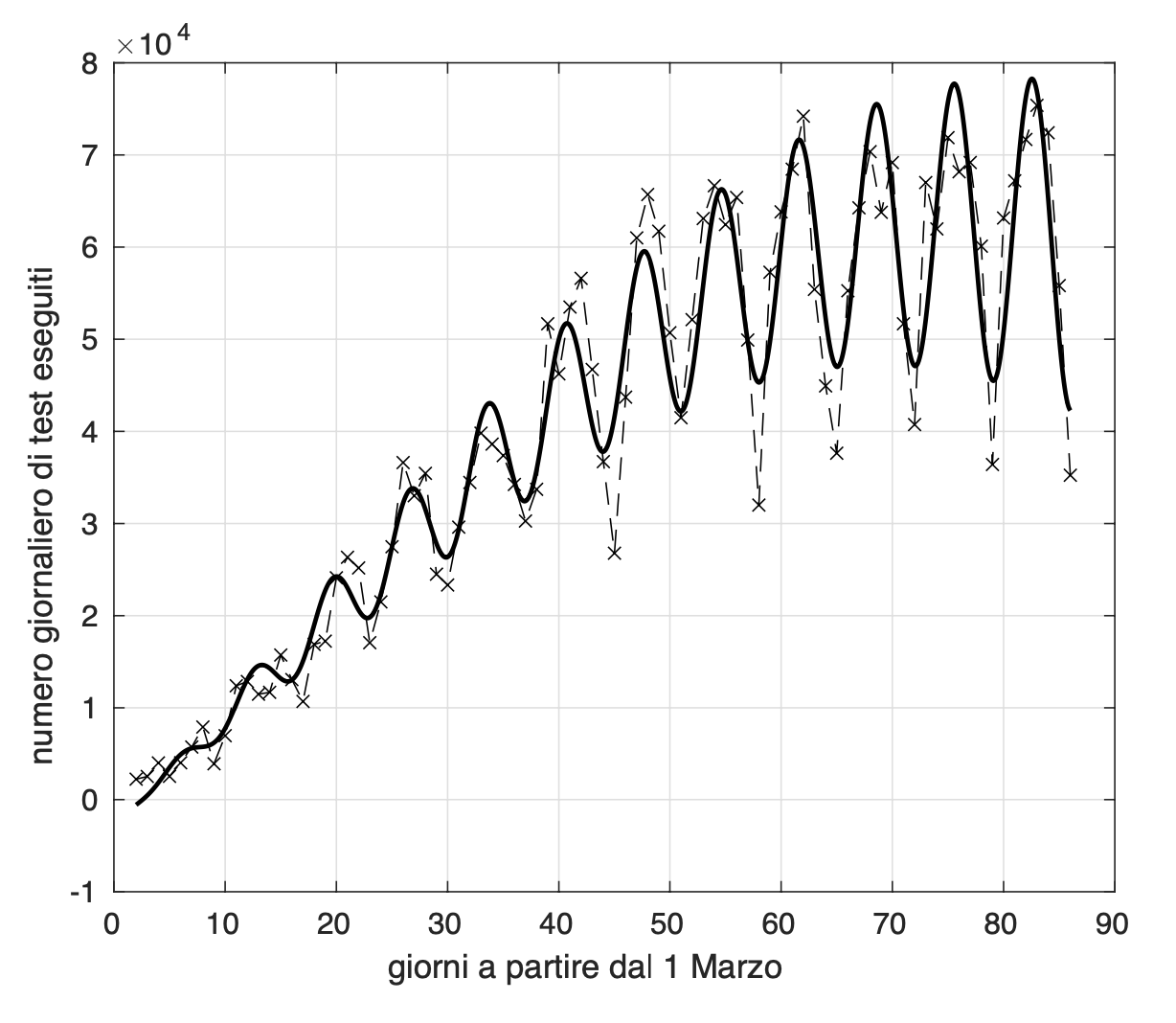
Per Lombardia, Liguria e la provincia di Trento oggi osserviamo una riduzione significativa dei valori dell'incidenza che ci aspettiamo sia dovuta al numero di campioni notevolmente piu' basso degli ultimi due giorni. Situazione da monitorare con molta attenzione.
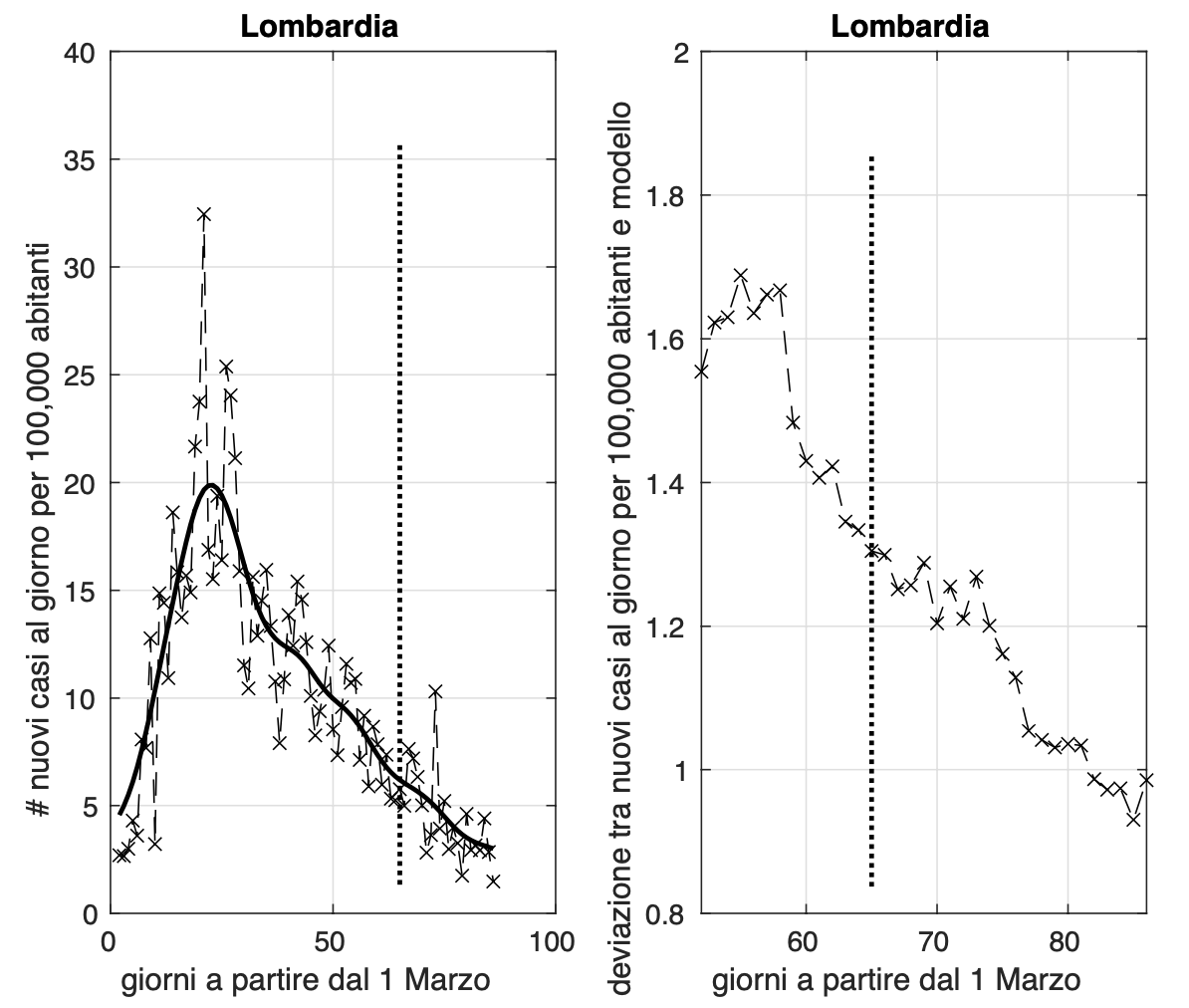
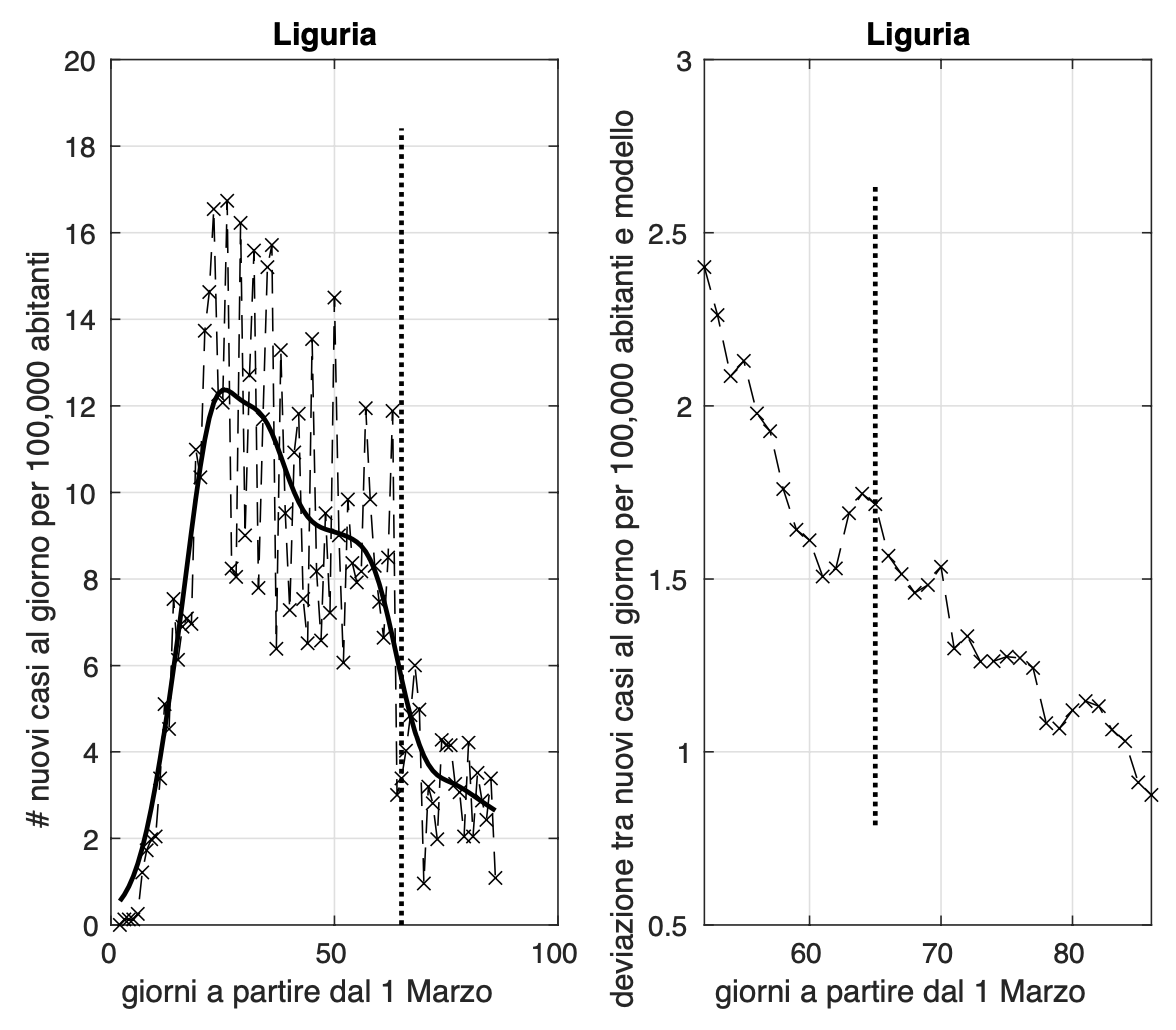
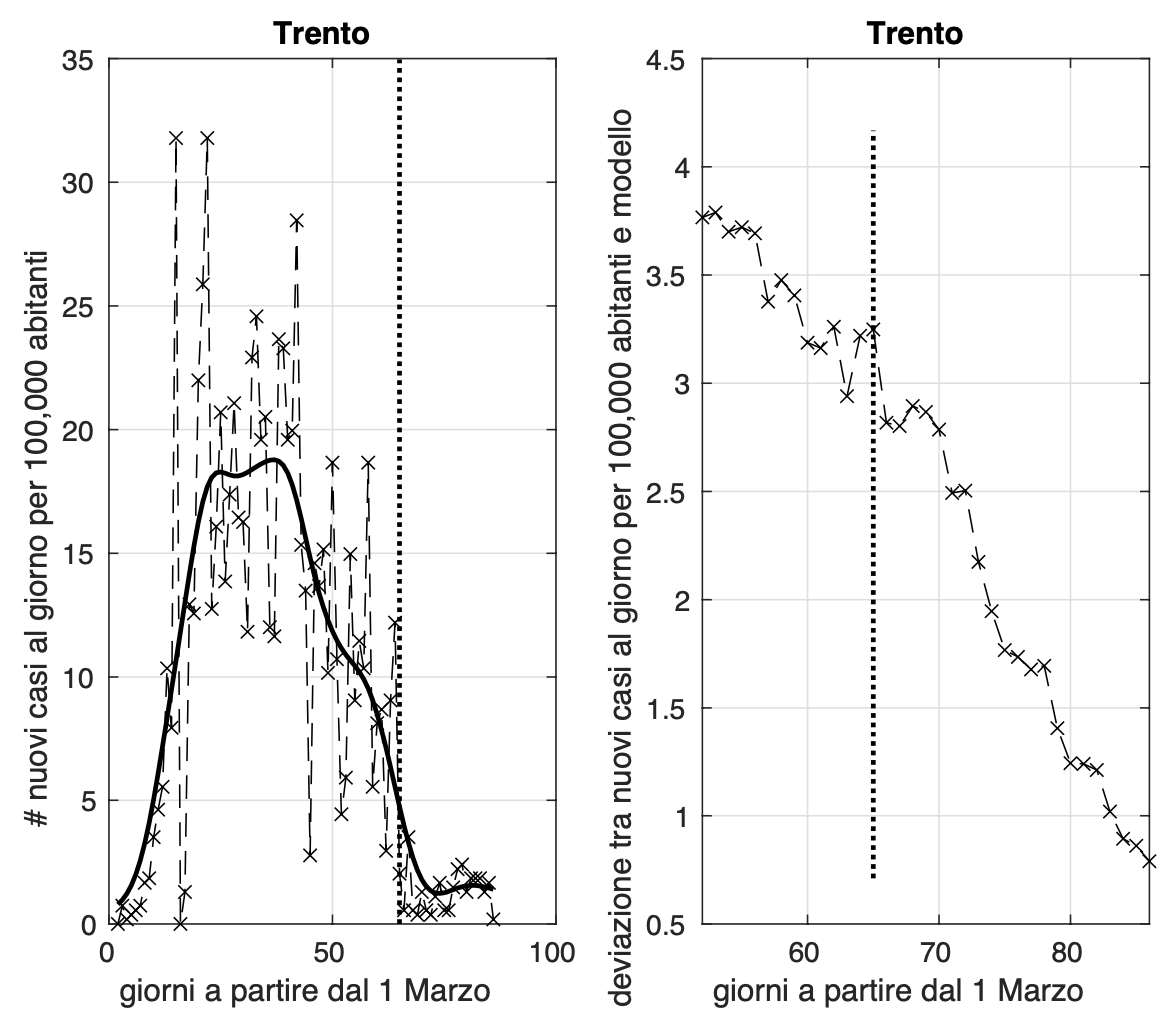
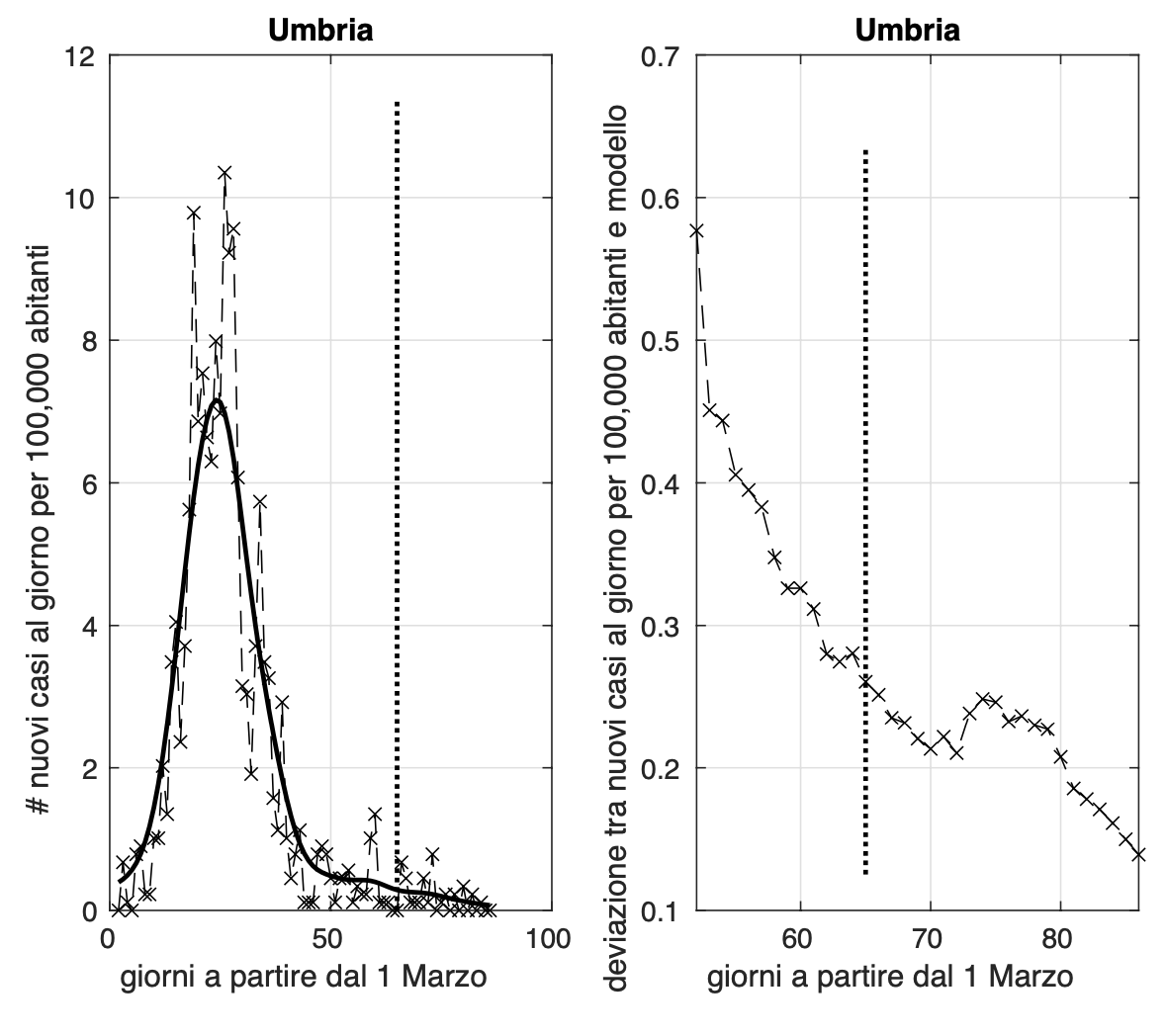
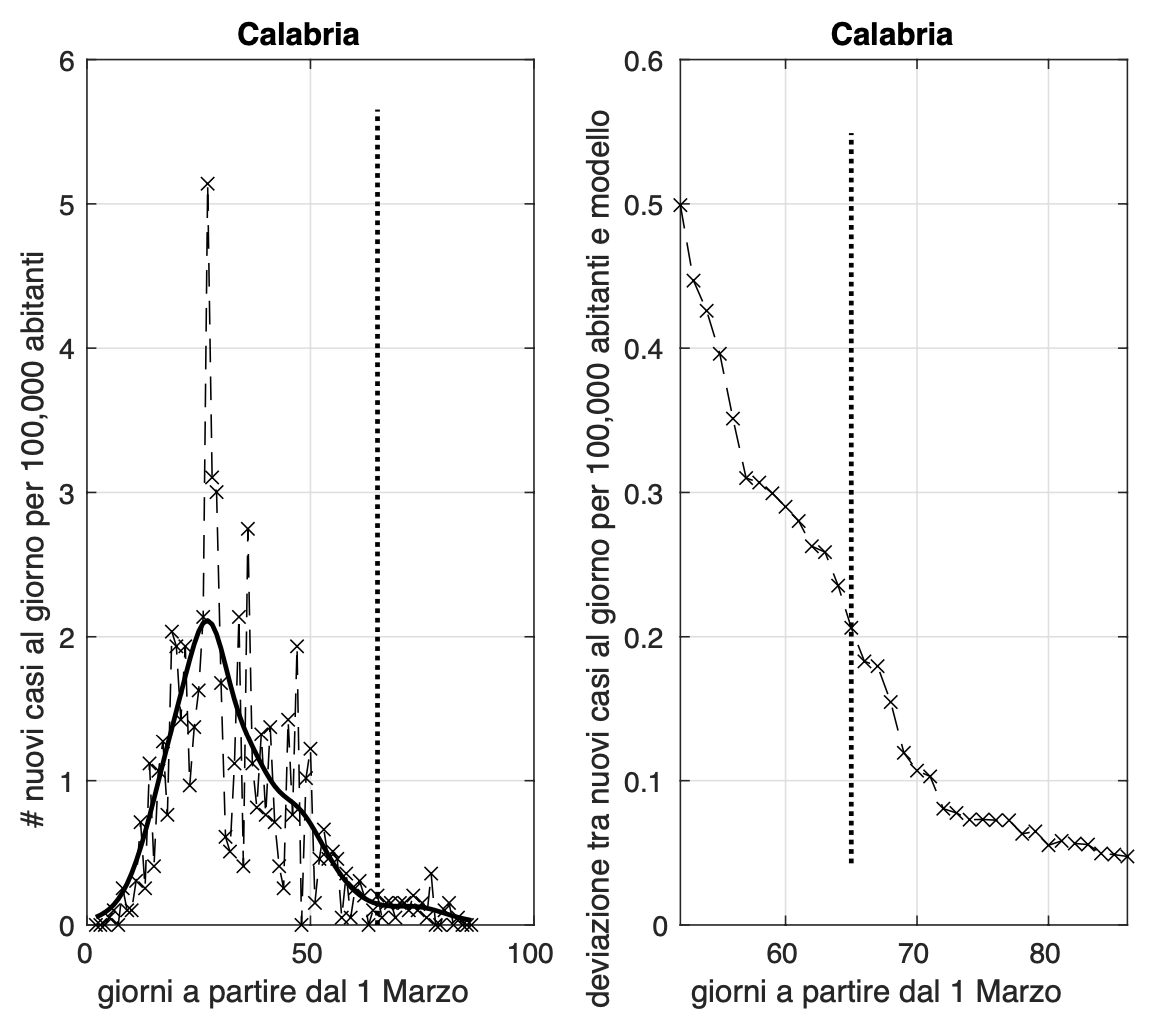
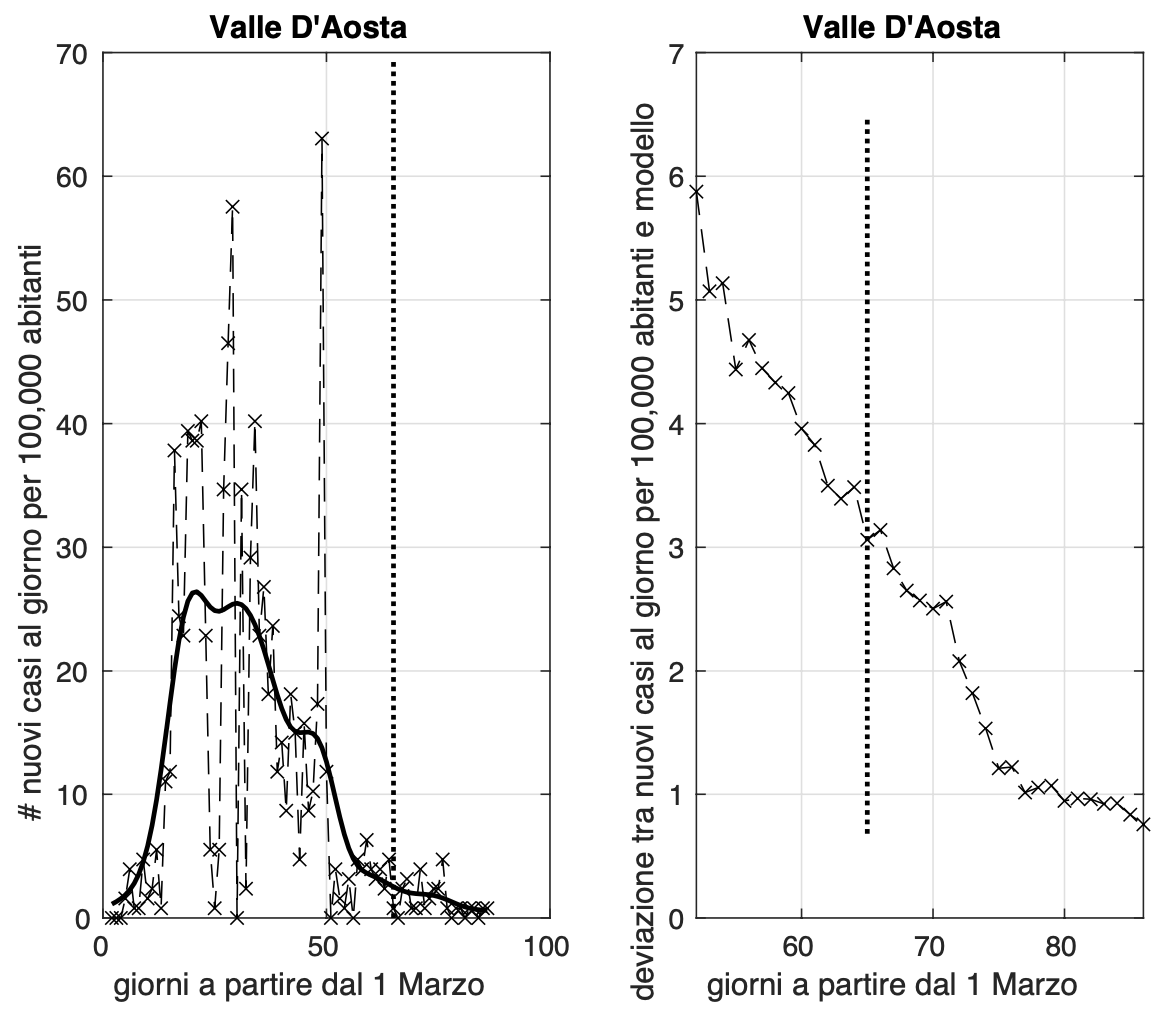
Ci sono quattro regioni dove la diffusione dell'epidemia sembra essere terminata, prima fra esse, troviamo la Sardegna, seguita da Umbria, Calabria e Valle D'Aosta.

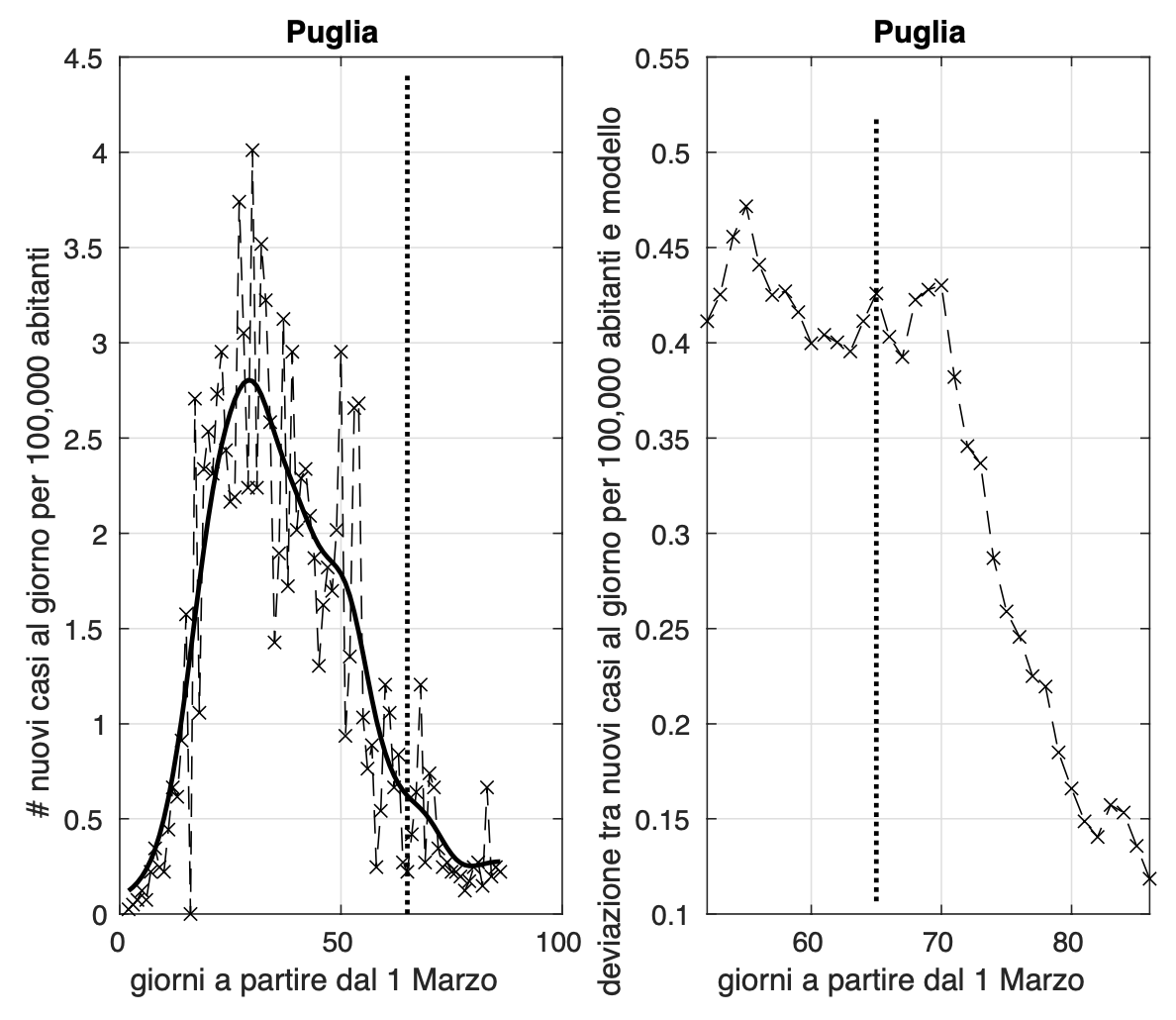
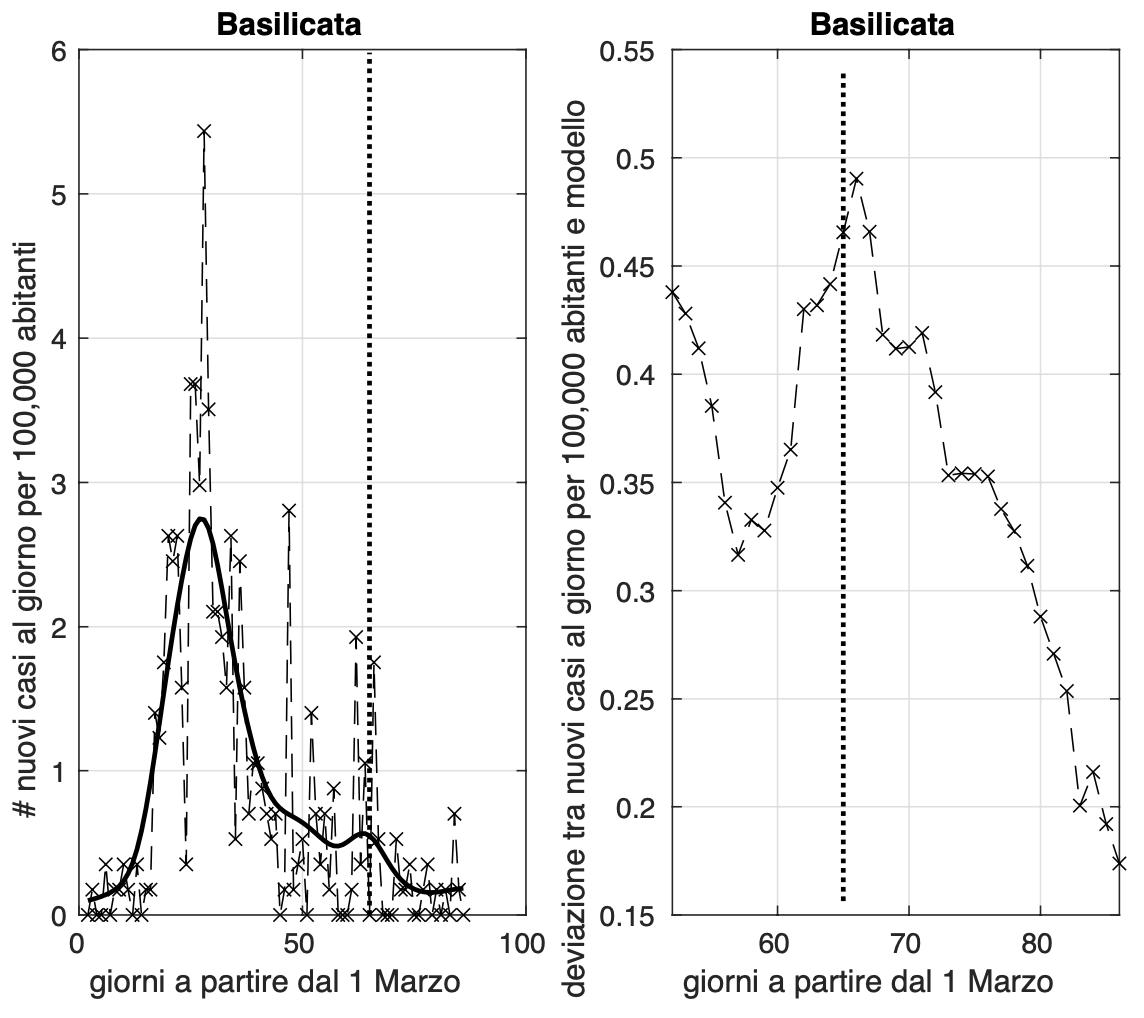
L'allarme per Puglia e Basilicata dovuto all'aumento significativo dell'incidenza degli ultimi due giorni sembra rientrato, ma il valore di oggi della Puglia non diminuisce rispetto ai valori precedenti agli ultimi due giorni, come accade invece per la Basilicata. Situazione comunque da monitorare.
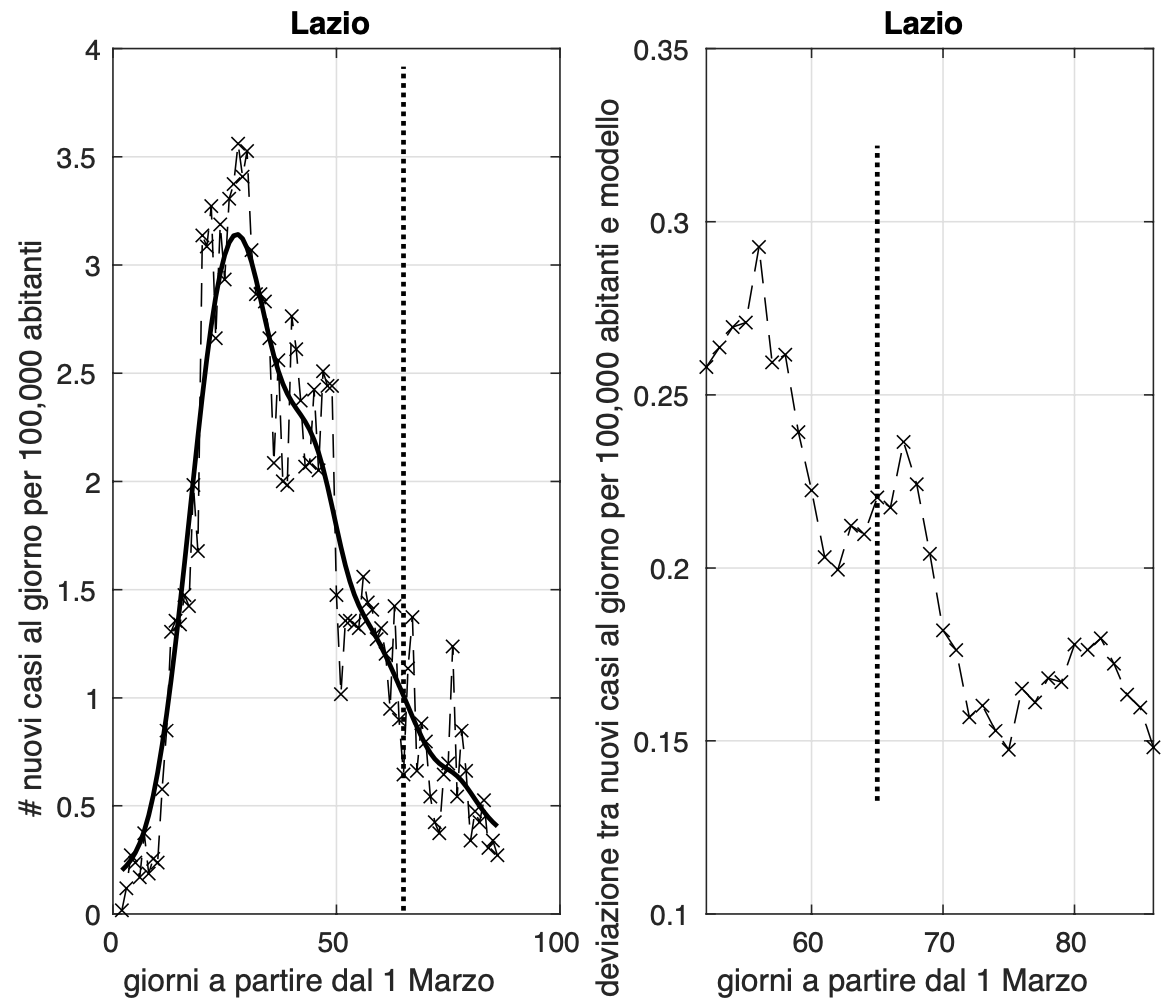
L'allarme per il Lazio sembra rientrato.
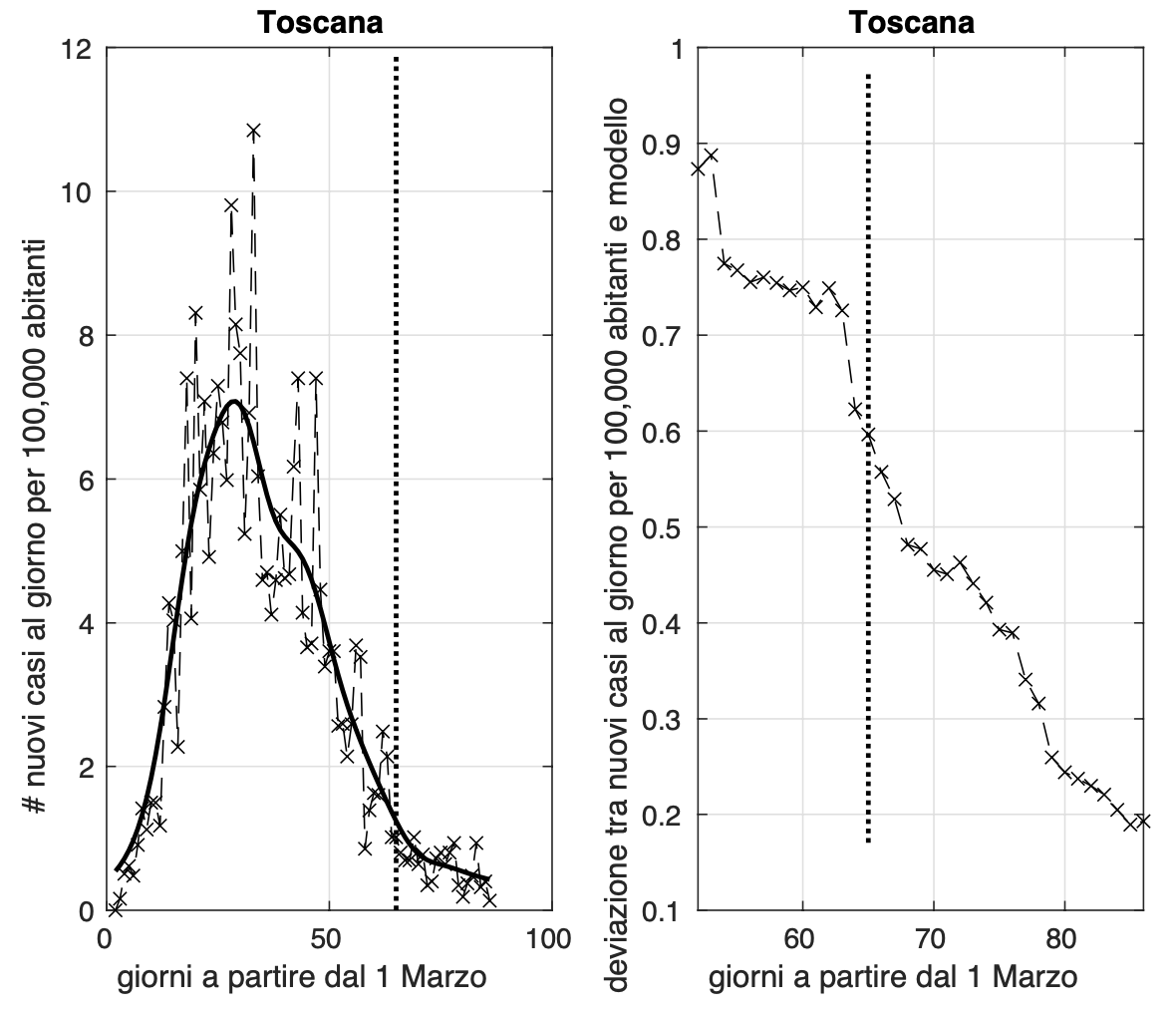
Lenta discesa dell'incidenza per regioni come la Campania, la Toscana ed il Friuli Venezia Giulia. Sembra rientrare l'allarme per le ultime due regioni dovuto all'aumento nei giorni scorsi. Utile osservare cosa accade nei prossimi giorni.
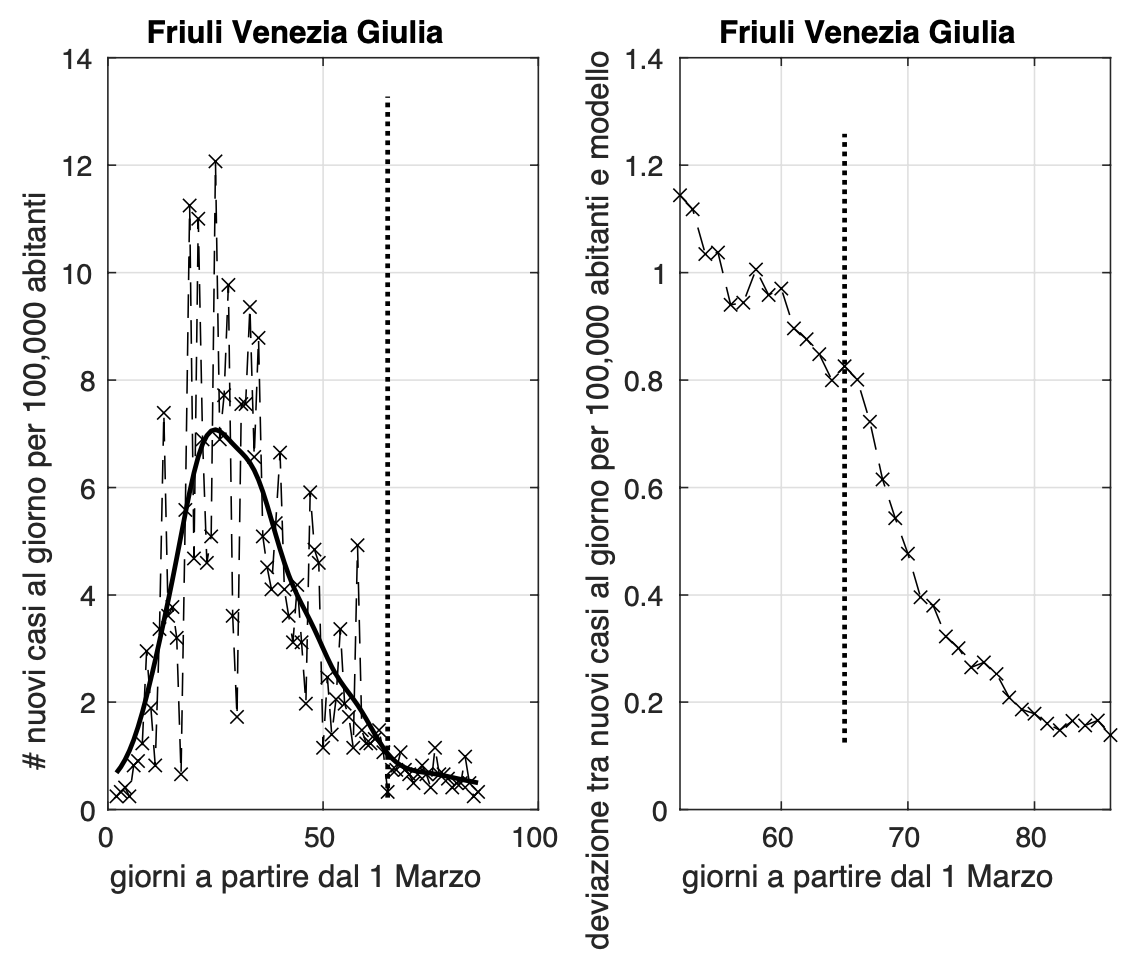 Sembra definitivamente rientrato l'allarme per il Molise, dove oggi l'incidenza è nulla. Anche la varianza continua a diminuire. Osserveremo cosa succede nei prossimi giorni.
Sembra definitivamente rientrato l'allarme per il Molise, dove oggi l'incidenza è nulla. Anche la varianza continua a diminuire. Osserveremo cosa succede nei prossimi giorni.
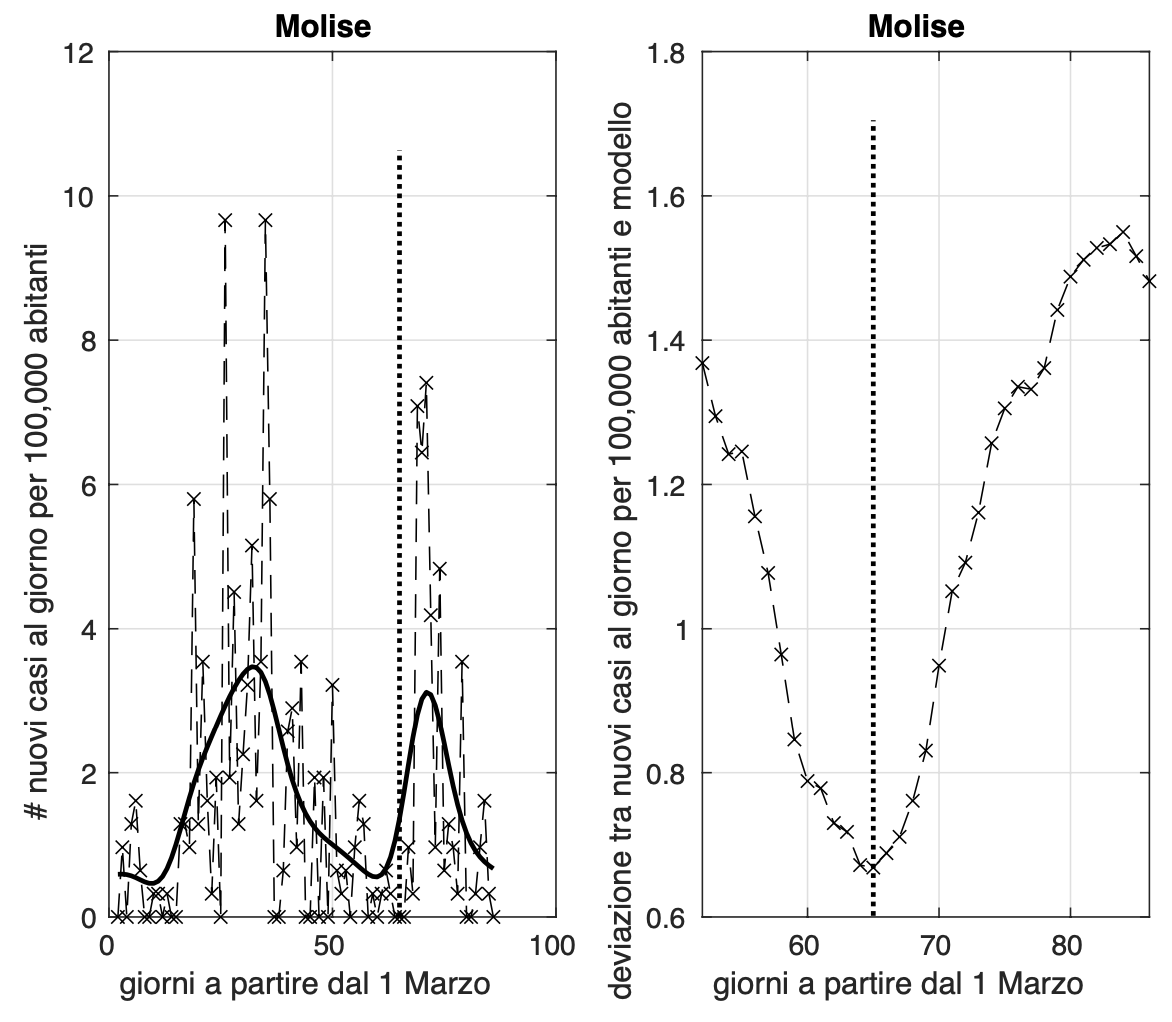
Dopo aver simato per ciascuna regione il modello per l'andamento temporale dell'incidenza e calcolato la sua varianza, possiamo utilizzare i valori finali delle due quantità per formare dei "gruppi" di regioni con valori "vicini". Questo può essere fatto ad esempio con l'algoritmo del clustering gerarchico che minimizza localmente la somma delle varianze all'interno dei gruppi delle grandezze considerate. Nella figura seguente è illustrato tramite il "dendrogramma" il risultato ottenuto. Osserviamo l'evidenza di tre gruppi:
- Liguria, Lombardia, Molise, Piemonte, Trento e Valle D'Aosta dove i valori delle due grandezze sono grandi;
- Abruzzo, Bolzano, Emilia Romagna, Friuli Venezia Giulia, Lazio, Marche, Toscana e Veneto, con valori intermedi;
- Basilicata, Calabria, Campania, Puglia, Sicilia, Sardegna ed Umbria, con valori bassi.
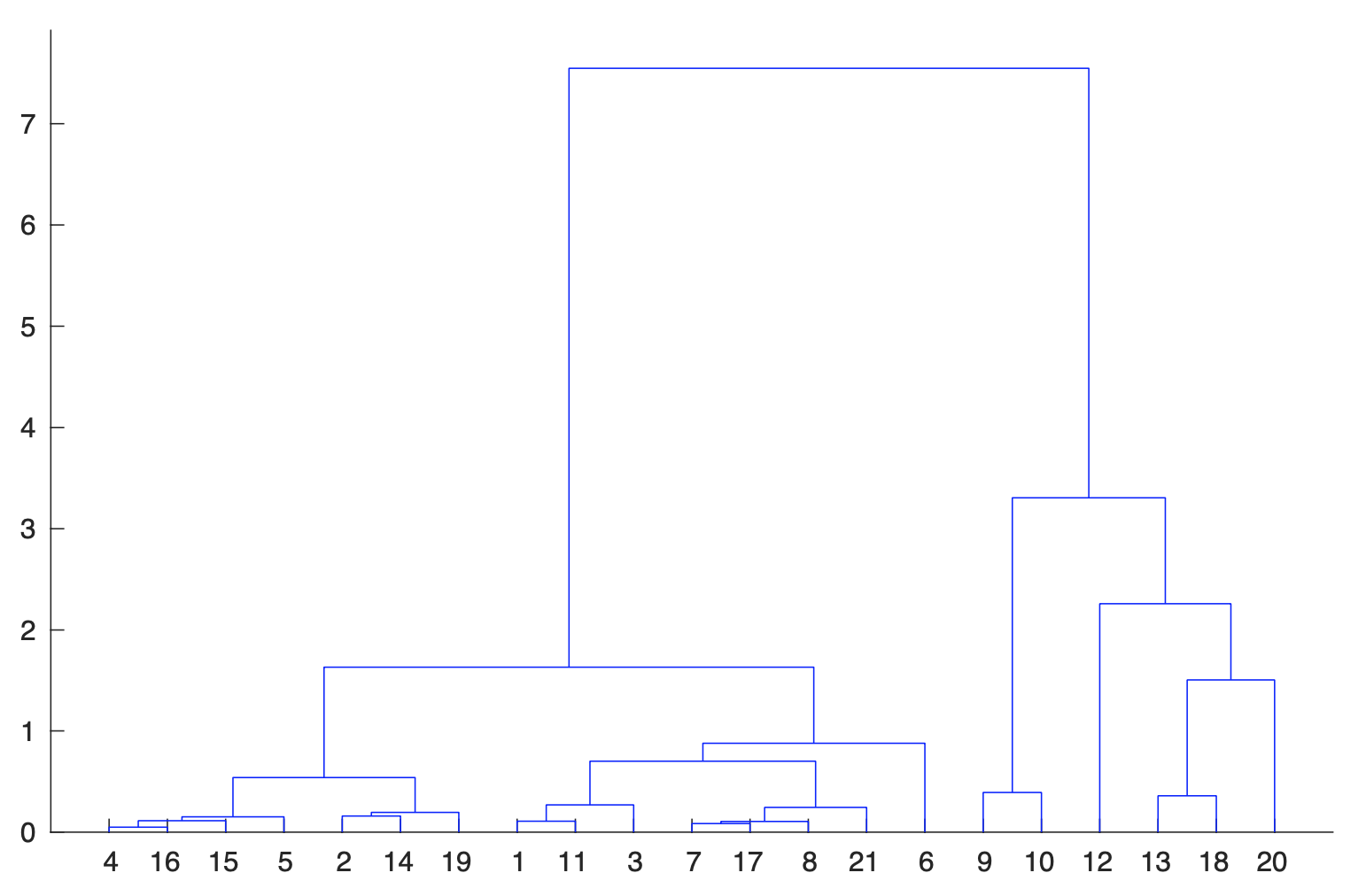
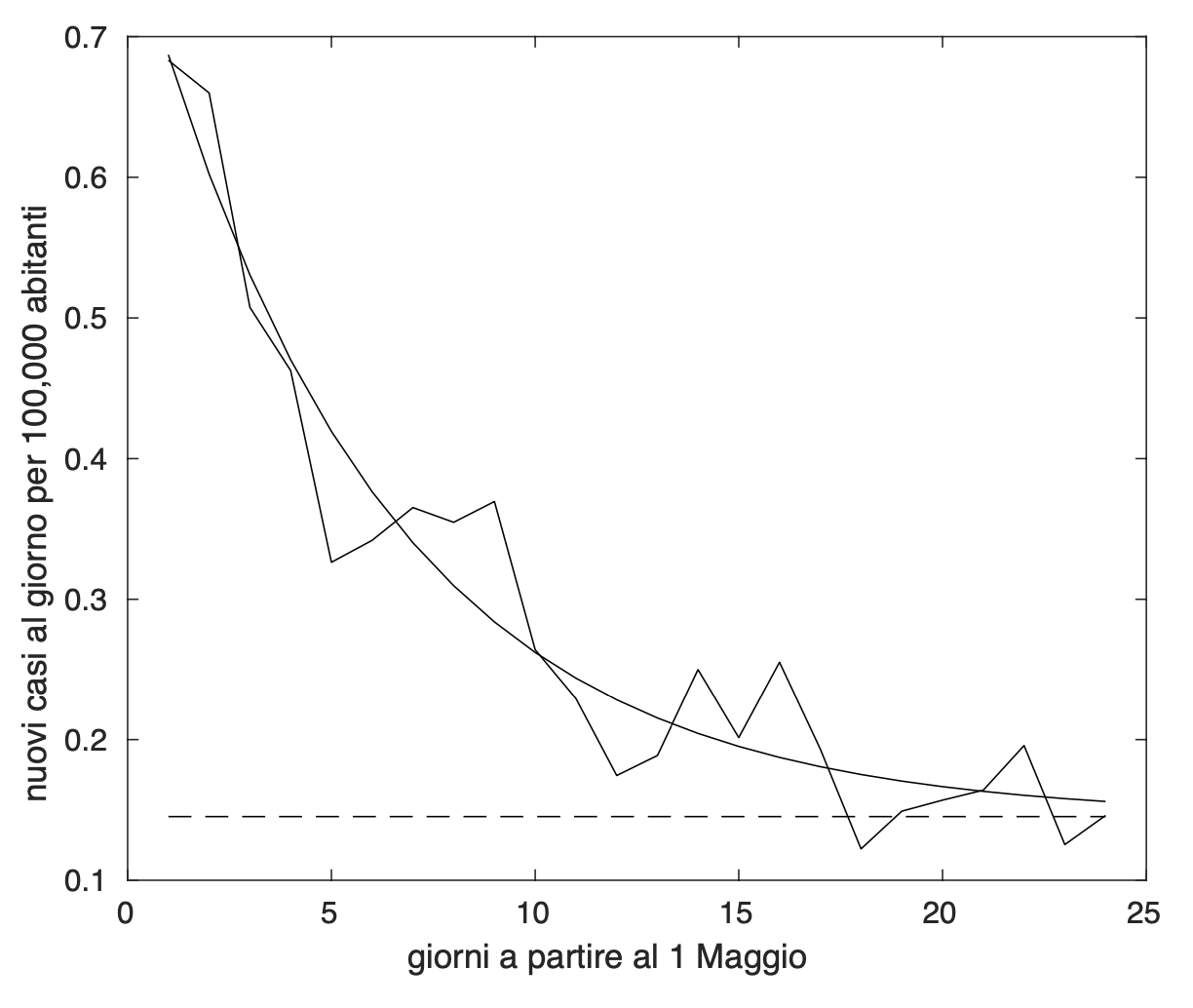
La curva dell'incidenza "media" nelle regioni del secondo gruppo mostra che il valore limite al quale converge sembra maggiore di zero. E' come se ci fosse un livello di contagio che non si riesce ad eliminare
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
Analisi dei dati epidemiologici del coronavirus in Italia (al 24 maggio)
- 8210 letture
In questo documento sono descritti alcuni risultati relativi all’analisi dei dati dell'epidemia di Covid-19 in Italia a livello regionale. I dati utilizzati sono stati scaricati dal sito https://github.com/pcm-dpc/COVID-19/tree/master/dati-regioni.
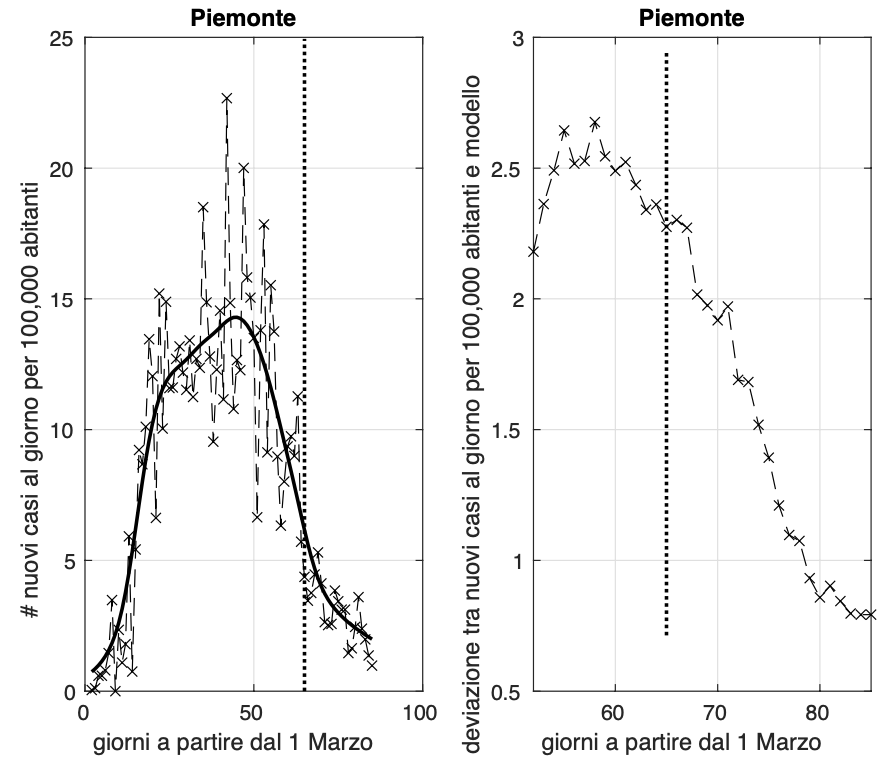
Allo scopo di individuare dei precursori dell'aumento di attività di diffusione dell'epidemia, abbiamo considerato la sequenza temporale dei valori misurati dell'incidenza di Covid-19, ossia il numero di nuovi casi positivi al giorno. Per rendere più facilmente confrontabili i risultati delle diverse regioni, abbiamo "normalizzato" l'incidenza rispetto alla popolazione della regione, rapportandola a 100,000 abitanti. A partire dai dati di ciascuna regione, abbiamo stimato i parametri di un modello teorico da noi ottenuto generalizzando quello "logistico". In alternativa, nei casi in cui ci siano variazioni improvvise e significative dell'incidenza, di cui il modello non è in grado di tener conto, abbiamo utilizzato un approccio "non parametrico". Questo è ad esempio il caso del Molise, che fino al 7 maggio si trovava in una fase avanzata dell'epidemia, con valori molto bassi dell'incidenza, che pero' l'8 maggio hanno subito un aumento consistente a causa di un focolaio, generato probabilmente da un funerale avvenuto il 30 aprile a Campobasso. A questo punto, due sono essenzialmente gli indicatori che abbiamo considerato.
Il primo riguarda la velocità con cui l'incidenza diminuisce andando verso lo zero. Se i valori misurati dell'incidenza sono molto bassi ma non diminuiscono o lo fanno con velocità inferiore al modello teorico, risultando in un eccesso di casi rispetto al modello negli ultimi giorni, consideriamo sospetta questa situazione. Il secondo precursore riguarda le "fluttuazioni" dei valori misurati dell'incidenza rispetto al modello teorico. Tali fluttuazioni sono quantificate tramite la loro varianza in una finestra temporale mobile di 21 giorni. Un aumento dei valori della varianza negli ultimi giorni è da noi considerato sospetto. Oltre alle fluttuazioni rispetto al modello, abbiamo anche considerato quelle rispetto ad un modello lineare locale stimato dai dati nella finestra, considerando per ogni tempo la varianza più bassa tra le due.
Il principio alla base di questo precursore è quello secondo il quale, prima che avvengano cambiamenti macroscopici di una grandezza (a livello della sua media) che descrive un sistema che sta uscendo fuori dall'equilibrio, e.g. la concentrazione di emoglobina nel sangue durante un sanguinamento gastrico in fase iniziale, possano avvenire delle variazioni nelle fluttuazioni rispetto al valor medio della grandezza considerata. Questo indicatore, ci ha permesso di prevedere esattamente il giorno del terremoto di Parkfield del 2004 (retrospettivamente usando i dati sismici fino a 100 giorni prima del mainshock) e prevederne uno nello stesso sito nel 2024.
Oggi 24 maggio ci sono sei regioni dove l'aumento del numero totale di casi positivi rispetto a dieci giorni fa è inferiore a venti, le stesse dei tre giorni scorsi: la Sardegna, la Calabria, l'Umbria, la Valle D'Aosta la Basilicata e la provincia di Bolzano. Inoltre, per le prime tre oggi l'incidenza è nulla. La Sardegna sembra vicina alla fine dell'epidemia, seguita dalla Calabria e dall'Umbria. D’altro canto, preoccupa la situazione di Lombardia, Liguria, Trento, Molise, Puglia e Lazio, dove i valori rimangono medio-alti o subiscono aumenti significativi.
Di seguito riportiamo i valori odierni dell’incidenza, ossia del numero di nuovi casi positivi al giorno per 100,000 abitanti
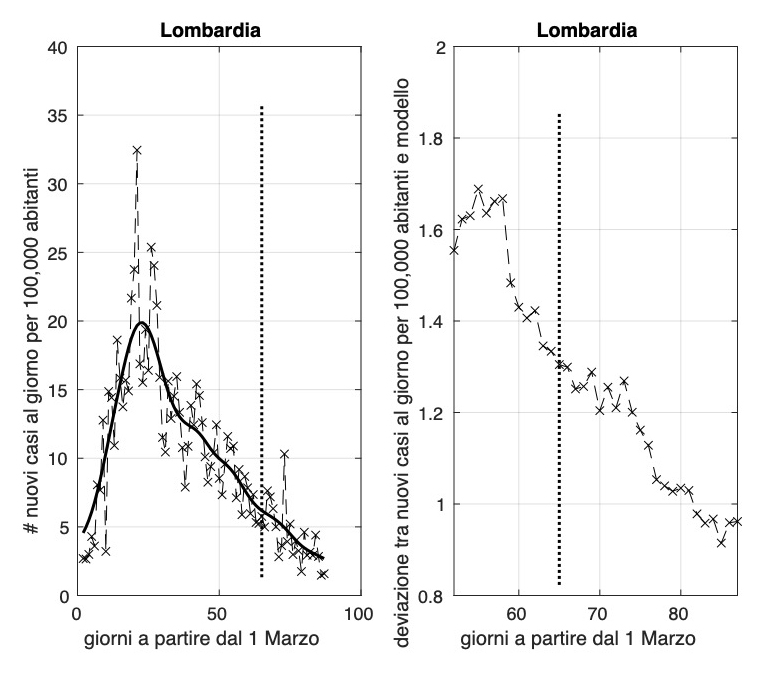
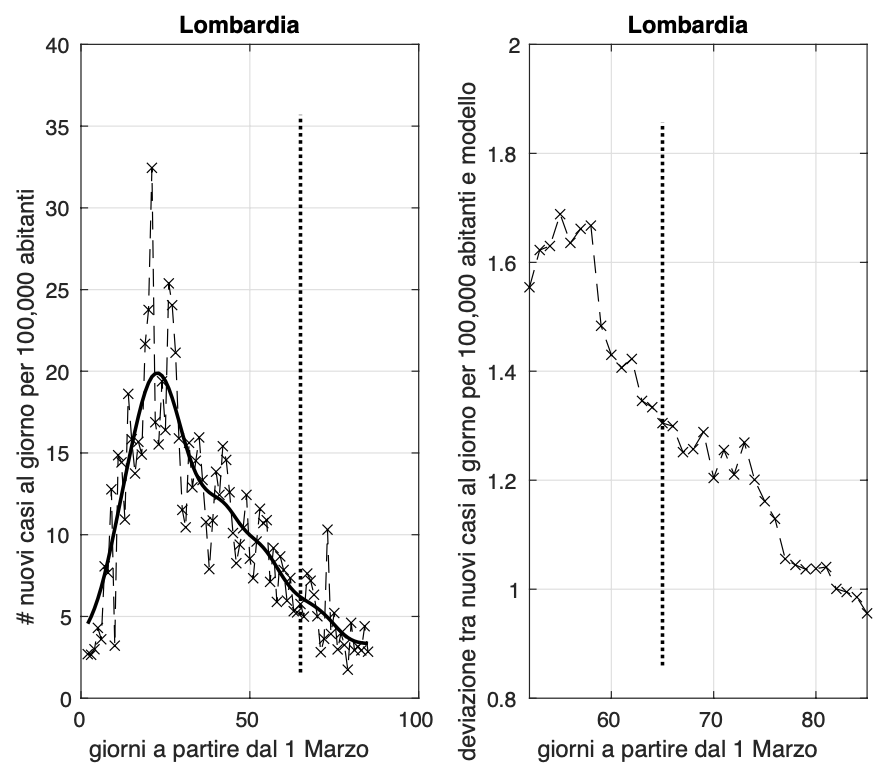
Rimane alto il valore dell'incidenza in Lombardia e Liguria (circa 2,8 e 3,4 nuovi casi al giorni per 100.000 abitanti rispettivamente), mentre fortunatamente il valore del Piemonte scende oggi poco sotto 1. I valori della Liguria da circa due settimane non scendono sotto il valore 2. Dopo il rilascio parziale del lockdown (4 maggio, segmento verticale), sembra che ci sia una riduzione della velocità con cui l'incidenza diminuisce verso lo zero. Situazione da monitorare con molta attenzione per Liguria e Lombardia.
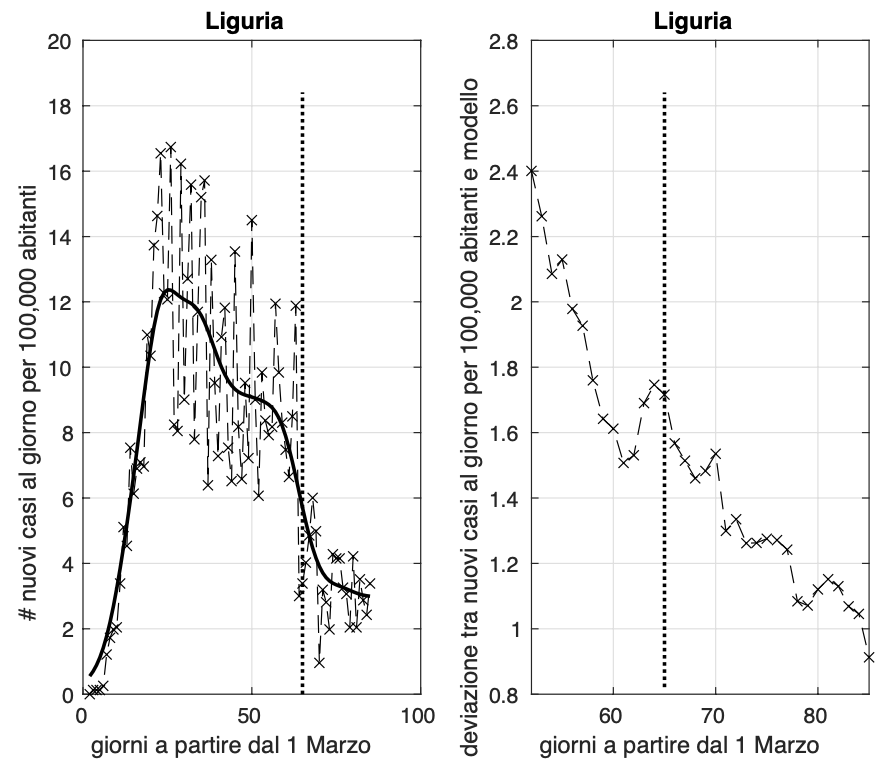
Trend in salita purtroppo negli ultimi dieci giorni per la provincia di Trento, con un valore medio dell’incidenza negli ultimi quattro giorni attorno a 1.6 nuovi casi al giorno per 100,000 abitanti. Situazione da monitorare con molta attenzione.
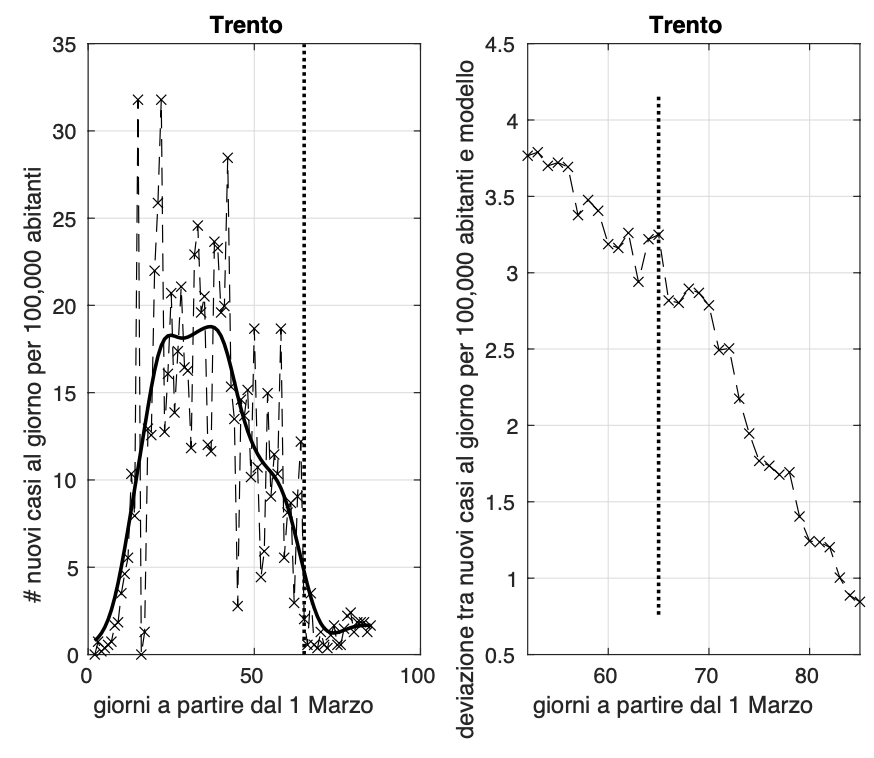
Gli incrementi dell'incidenza avvenuti negli ultimi due giorni in Puglia e Basilicata sembra siano stati sporadici. Comunque la situazione va monitorata nei prossimi giorni.
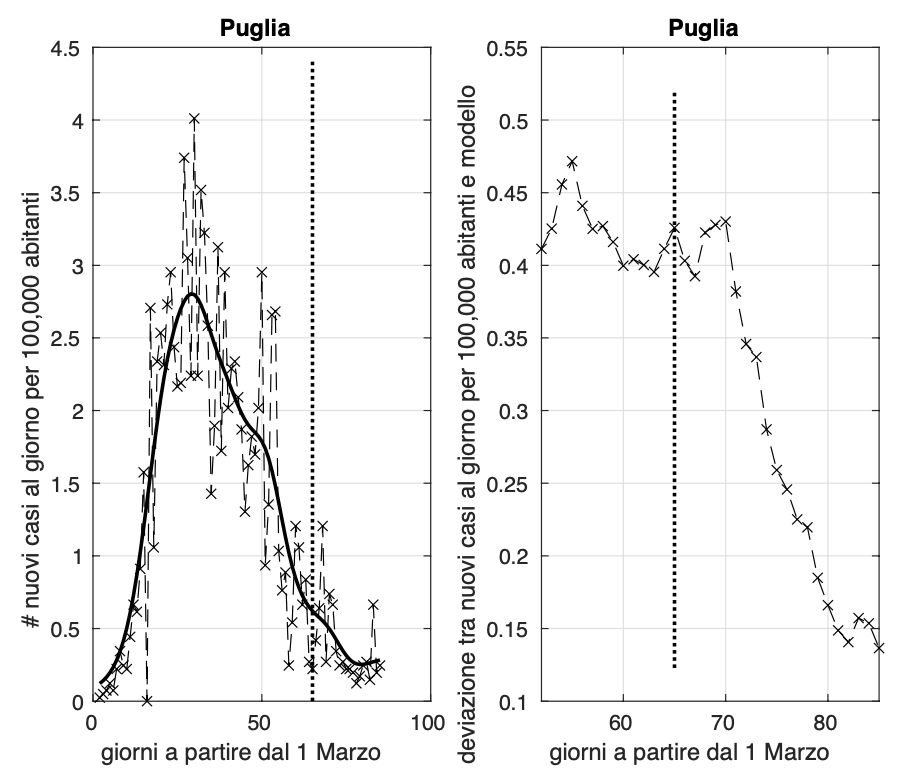

Sembra aumentare la velocià con cui va a zero l'incidenza in Calabria e Umbria, dove negli ultimi dieci giorni circa c'è un alternanza giornaliera di valori nulli.
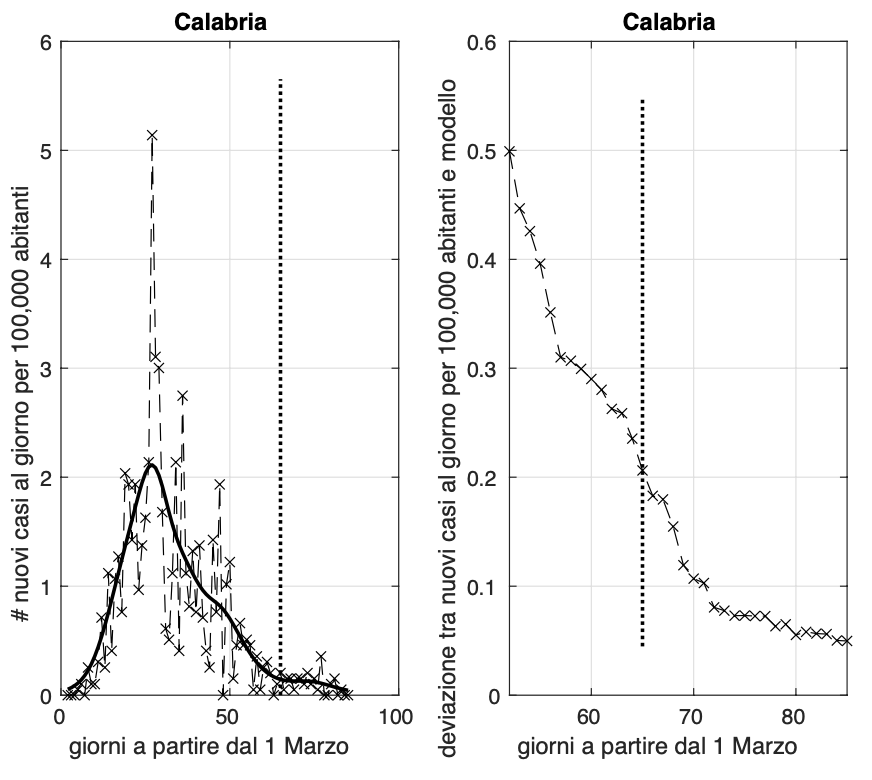

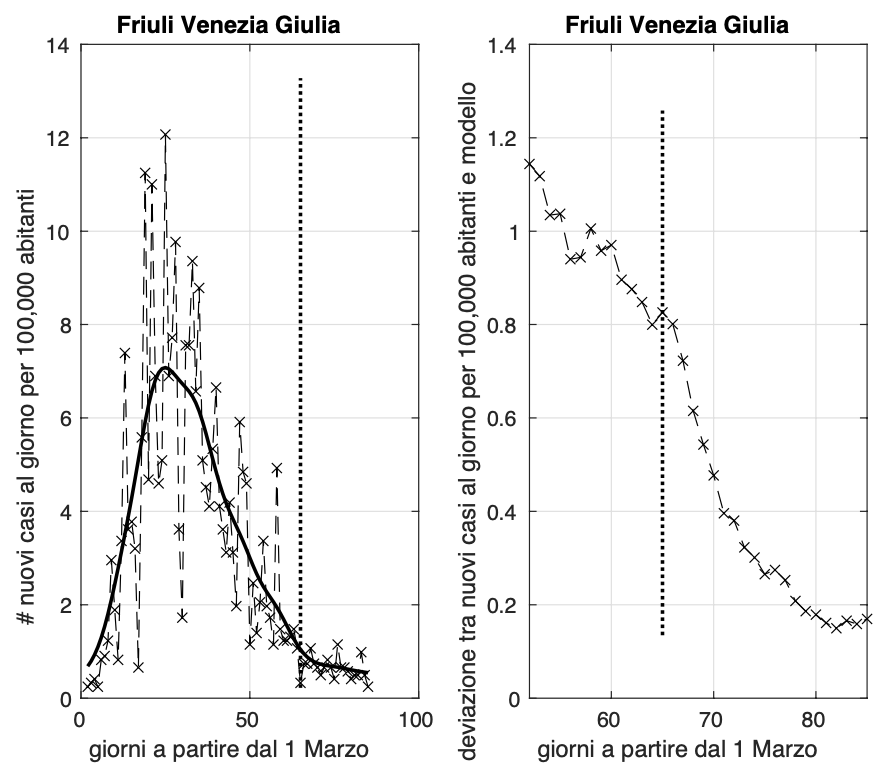
Lenta discesa dell'incidenza per regioni come la Campania, la Toscana ed il Friuli Venezia Giulia. Sembra rientrare l'allarme per le ultime due regioni dovuto all'aumento nei giorni scorsi. Utile osservare cosa accade nei prossimi giorni.
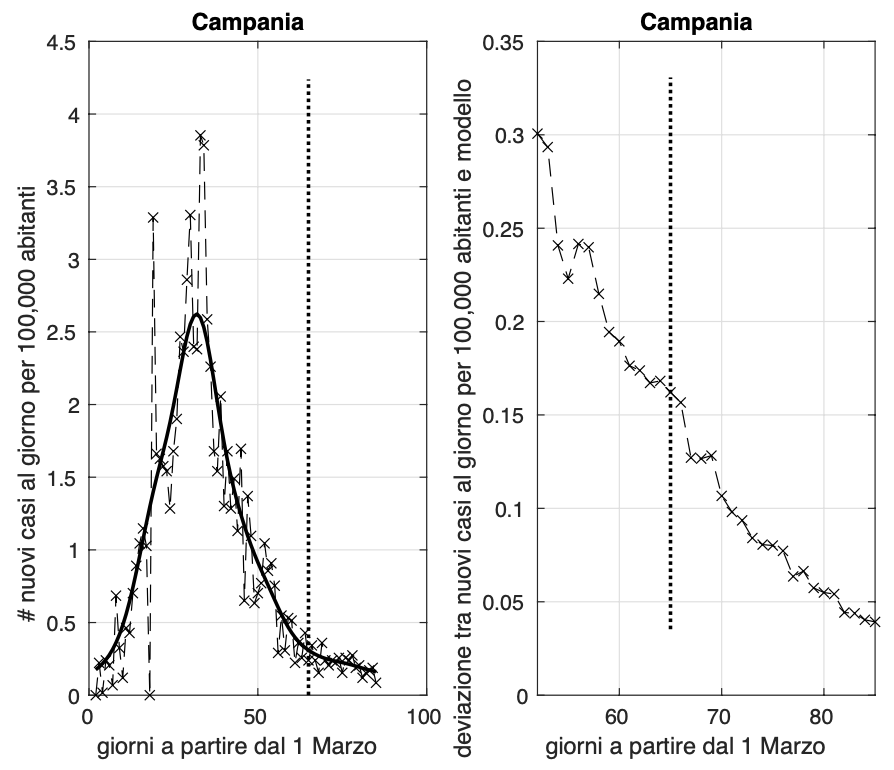
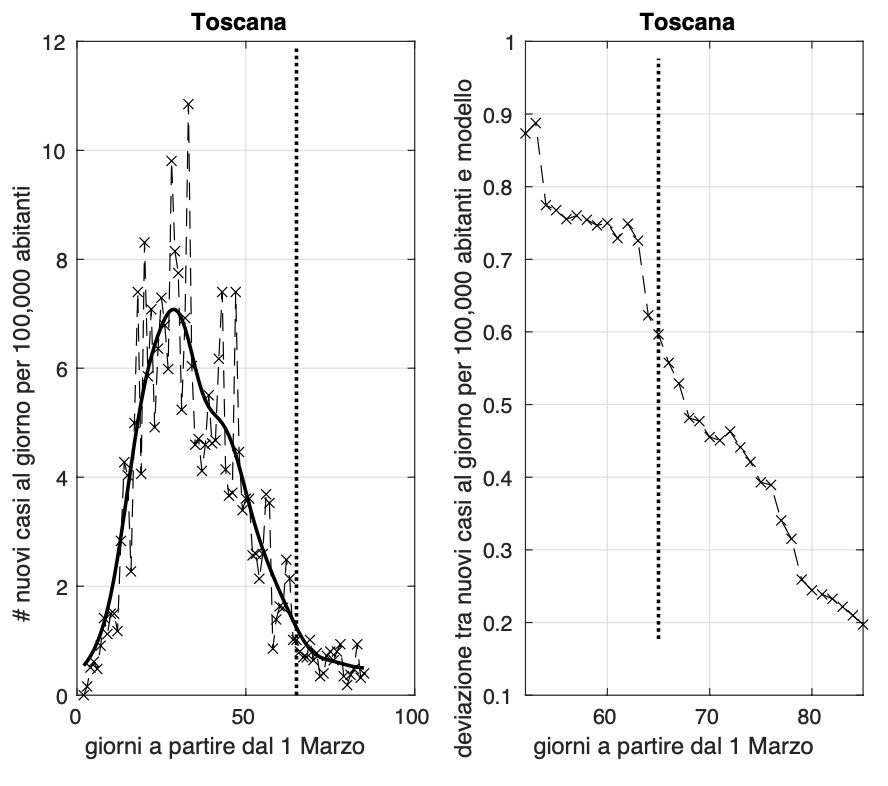
La situazione altalenante dell’incidenza nel Lazio vede ieri fortunatamente una diminuzione fino a circa 0,3 nuovi casi al giorno per 100.000, confermato anche oggi. Anche la varianza sembra essere tornata a diminuire.
Situazione da monitorare.
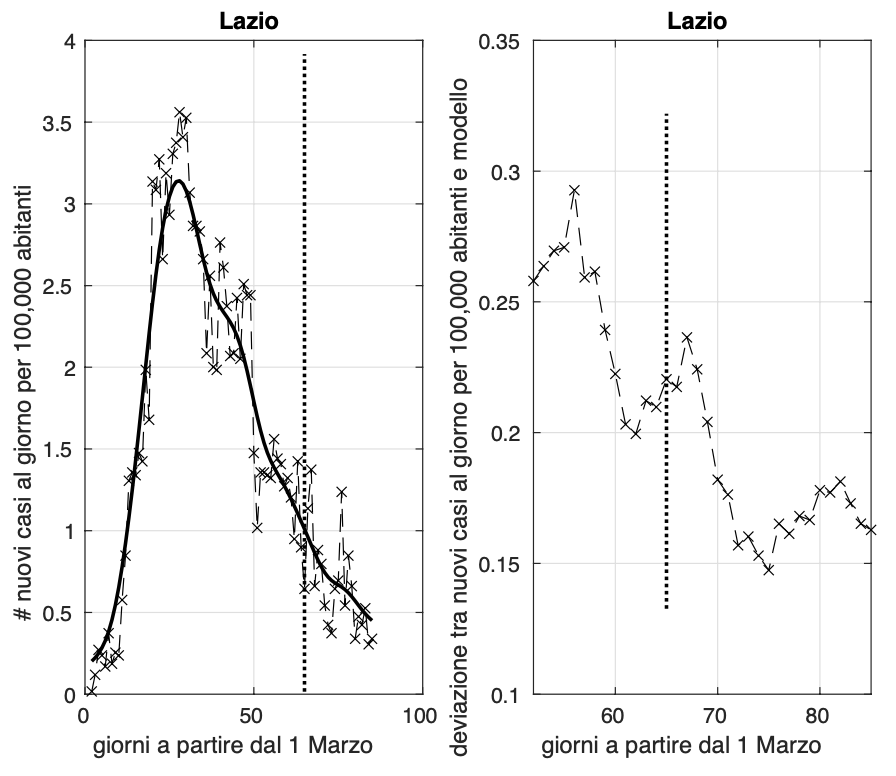
Per il Molise, dopo l'aumento significativo dell'8 maggio e giorni successivi, il ritorno a valori bassi nei giorni 14-17 maggio, il rialzo significativo del 18 maggio, raggiungendo un valore attorno a 3,5 nuovi casi al giorno per 100.000 abitanti, l'incidenza nulla del 19 e 20 maggio, il valore degli ultimi tre giorni attorno a 0,3, 1 e 1,6, oggi osserviamo una diminuzione fino ad un valore attorno a 0,3. Anche la varianza sembra essere tornata a diminuire. Situazione da tenere sotto osservazione.
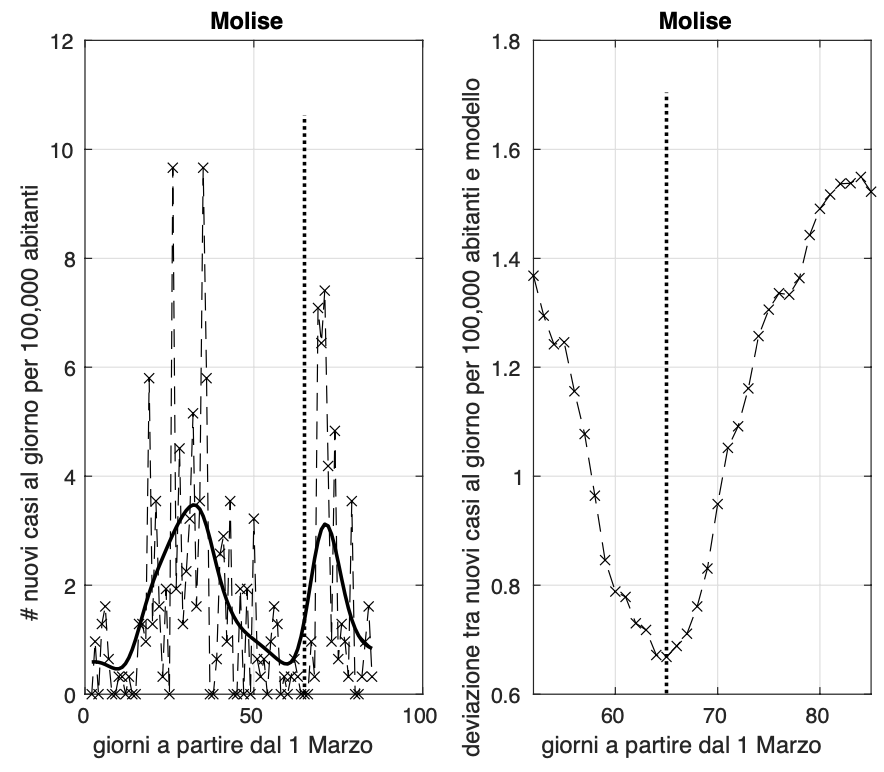
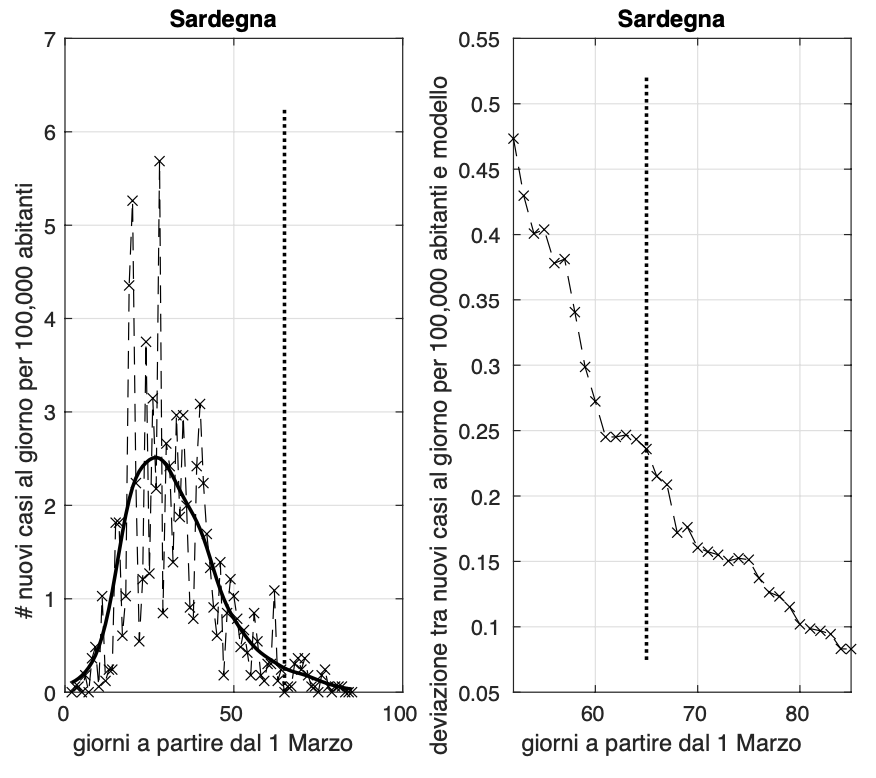
Sembra che la Sardegna sia vicina alla fine dell'epidemia.
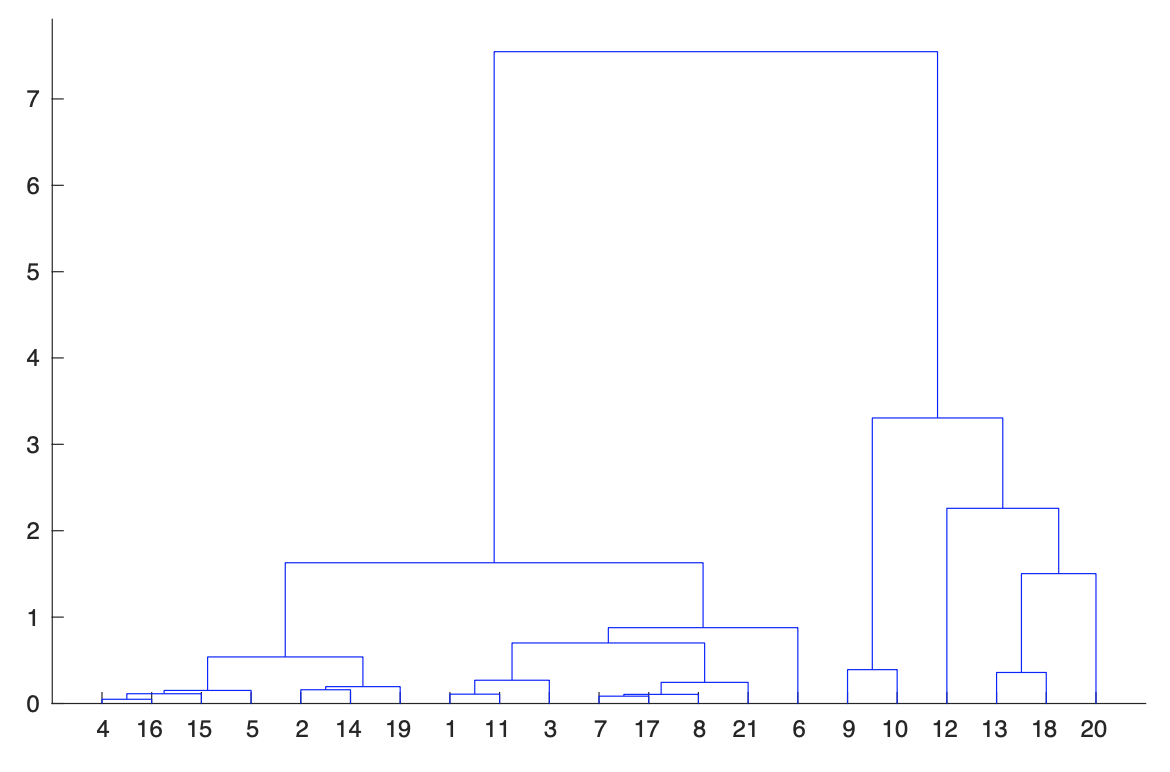
Dopo aver simato per ciascuna regione il modello per l'andamento temporale dell'incidenza e calcolato la sua varianza, possiamo utilizzare i valori finali delle due quantità per formare dei "gruppi" di regioni con valori "vicini". Questo può essere fatto epr esempio con l'algoritmo del clustering gerarchico che minimizza localmente la somma delle varianze all'interno dei gruppi delle grandezze considerate. Nella figura seguente è illustrato tramite il "dendrogramma" il risultato ottenuto. Osserviamo l'evidenza di tre gruppi:
- Liguria, Lombardia, Molise, Piemonte, Trento e Valle D'Aosta dove i valori delle due grandezze sono grandi;
- Abruzzo, Bolzano, Emilia Romagna, Friuli Venezia Giulia, Lazio, Marche, Toscana e Veneto, con valori intermedi;
- Basilicata, Calabria, Campania, Puglia, Sicilia, Sardegna ed Umbria, con valori bassi.
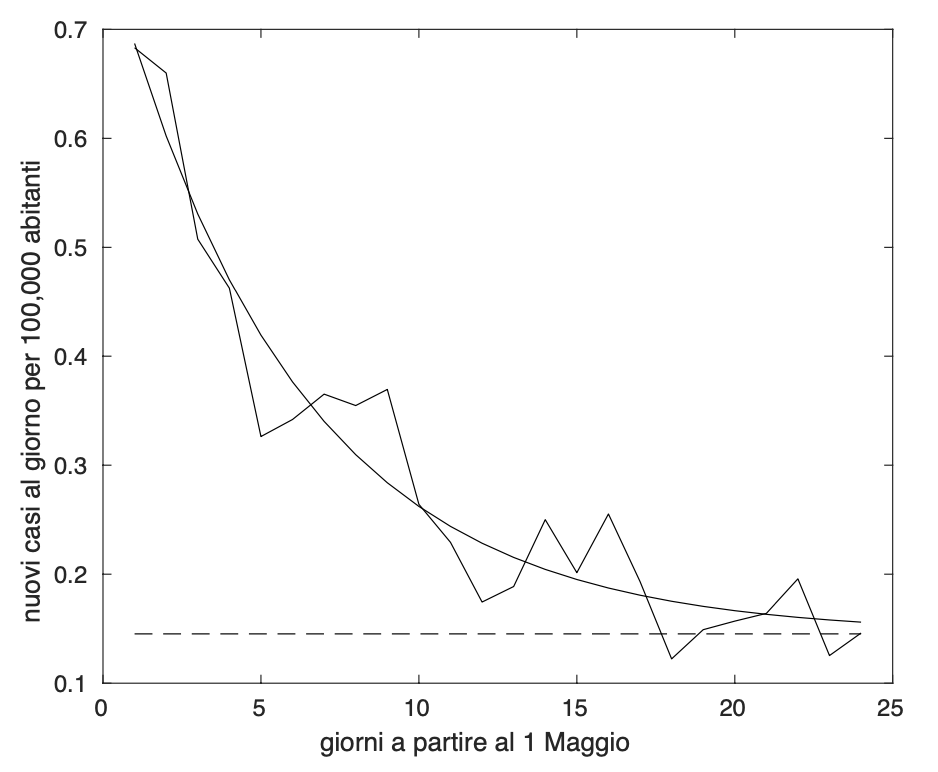
La curva dell'incidenza "media" nel gruppo 2 delle regioni mostra che il valore limite al quale converge sembra maggiore di zero.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
Analisi dei dati epidemiologici del coronavirus in Italia (al 4 maggio)
- 6969 letture
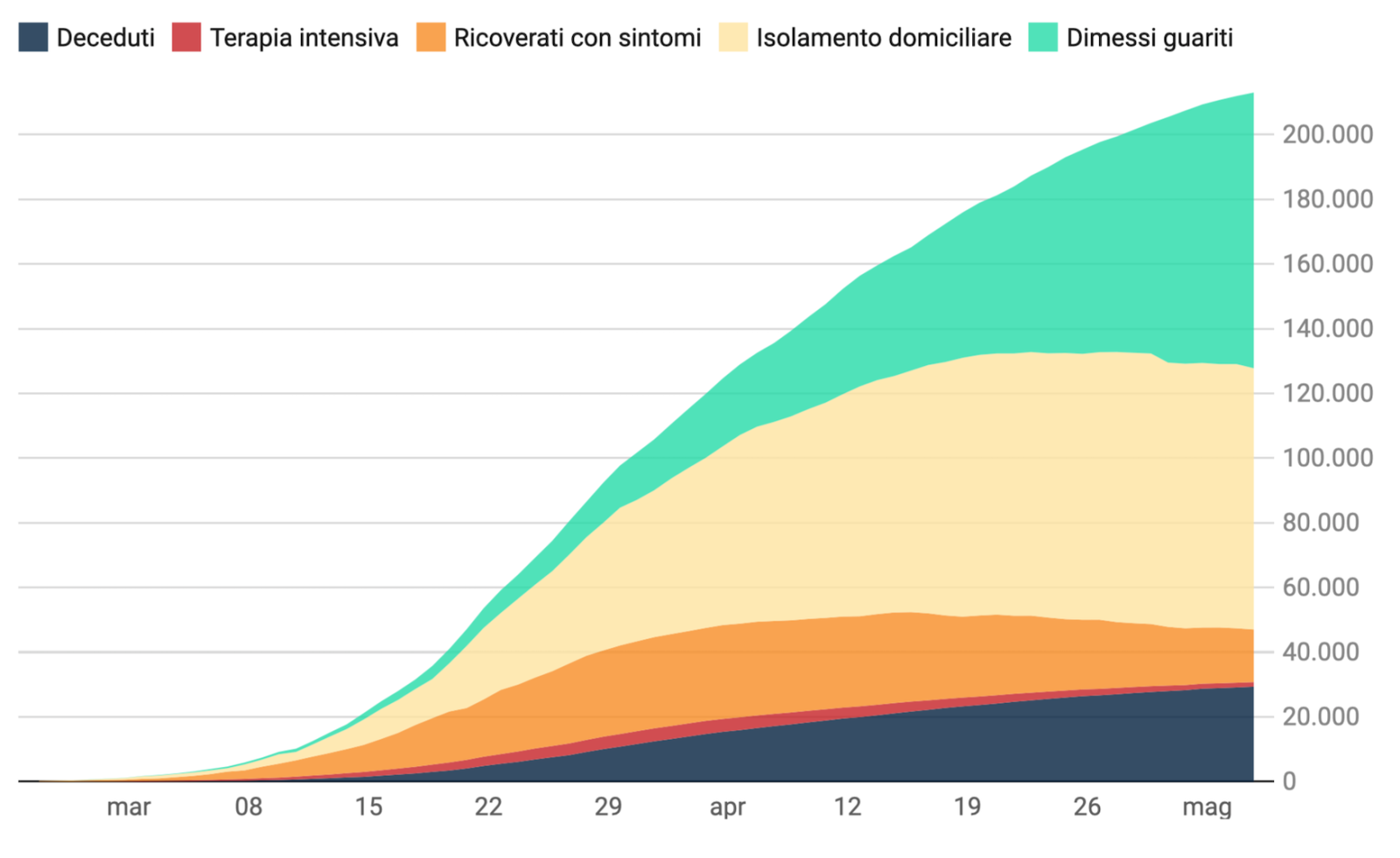
L’analisi delle sequenze temporali della frazione dei contagiati osservati rispetto alla popolazione della provincia rivela che finalmente tutte le 107 province presentano una diminuzione del tasso di crescita. Inoltre, si osservano tre regioni con un numero nullo di contagiati osservati al giorno: Umbria, Molise e Basilicata. A livello di province, ne troviamo 34 con numero nullo di nuovi contagiati osservati. Naturalmente, sappiamo che il primo giorno della settimana osserviamo spesso numeri più bassi a causa della ridotta attività di analisi dei tamponi nei giorni di fine settimana.
Possiamo comunque considerare le province dove nelle ultime due settimane si osserva un aumento percentuale del numero di contagiati osservati molto piccolo. Ne abbiamo individuate 19: L’Aquila (vedi figura 1), Teramo, Bolzano, Catanzaro, Crotone (vedi figura 2), Salerno, Ravenna (vedi figura 3), Udine, Frosinone, Mantova, Ancona, Campobasso, Sassari, Agrigento, Trapani (vedi figura 4), Siena, Perugia (vedi figura 5), Terni e Padova (vedi figura 6). Notiamo che cinque province sono al nord e le restanti 14 sono al centro e al sud. Questo ci dice una volta ancora che l’epidemia al centro e al sud si trova mediamente in fase più avanzata, ma al tempo stesso che sia al nord che al sud abbiamo delle variazioni tra province.
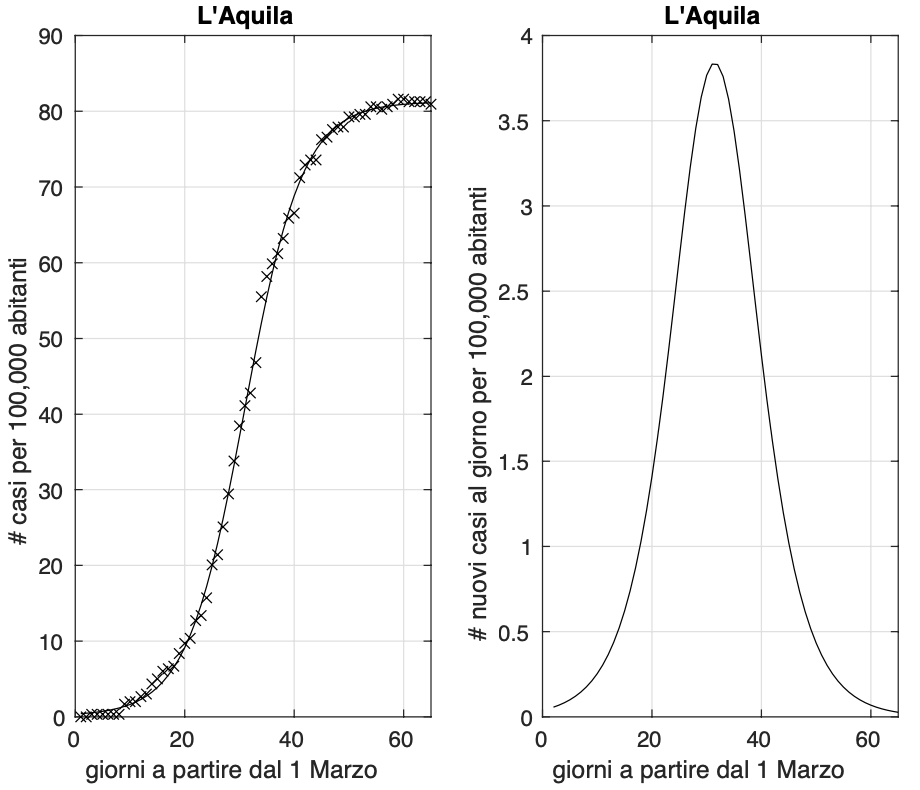
Figura 1. Sequenza del numero dei contagiati osservati nella provincia dell’Aquila. Il miglior fit con un modello logistico generalizzato è sovrapposto ai dati.
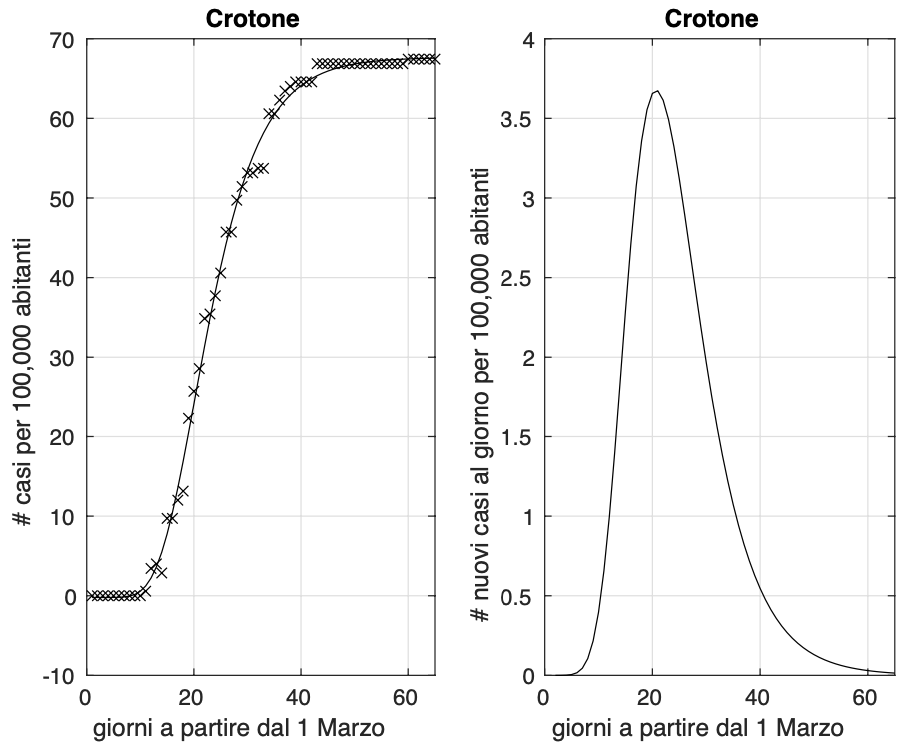
Figura 2. Sequenza del numero dei contagiati osservati nella provincia di Crotone. Il miglior fit con un modello logistico generalizzato è sovrapposto ai dati.
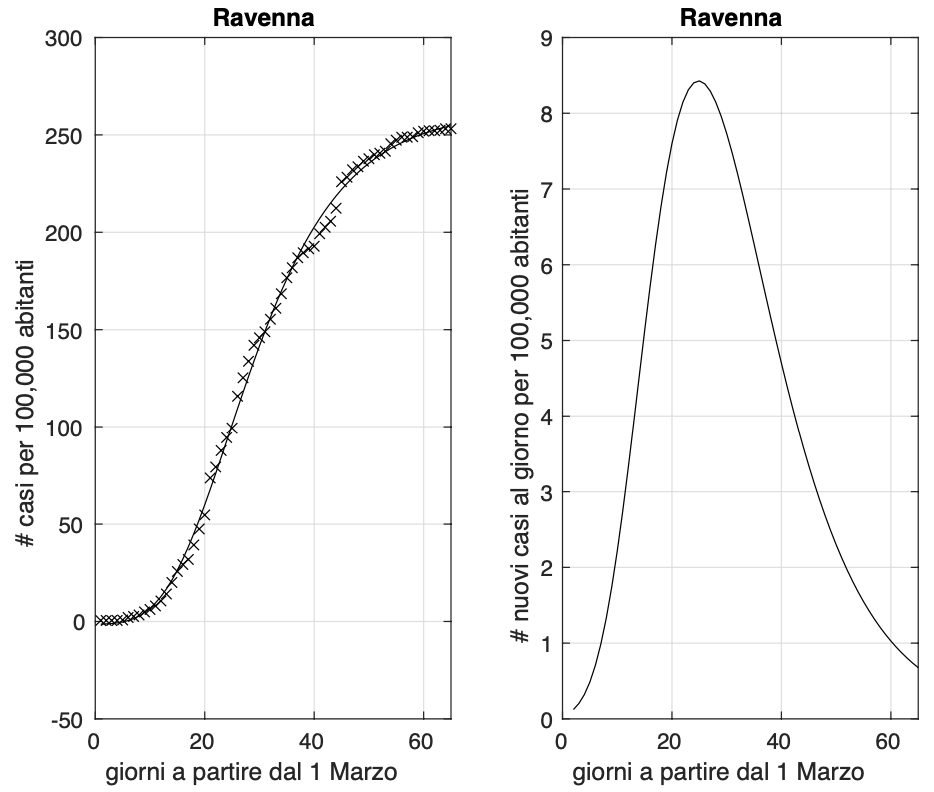
Figura 3. Sequenza del numero dei contagiati osservati nella provincia di Ravenna. Il miglior fit con un modello logistico generalizzato è sovrapposto ai dati.
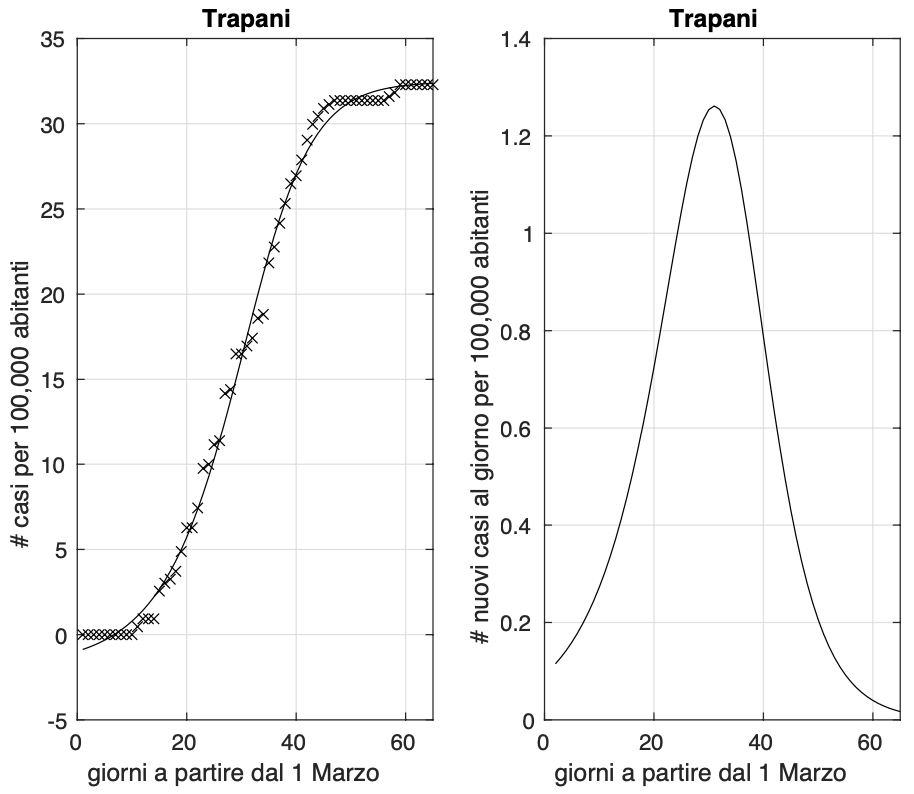
Figura 4. Sequenza del numero dei contagiati osservati nella provincia di Trapani. Il miglior fit con un modello logistico generalizzato è sovrapposto ai dati.
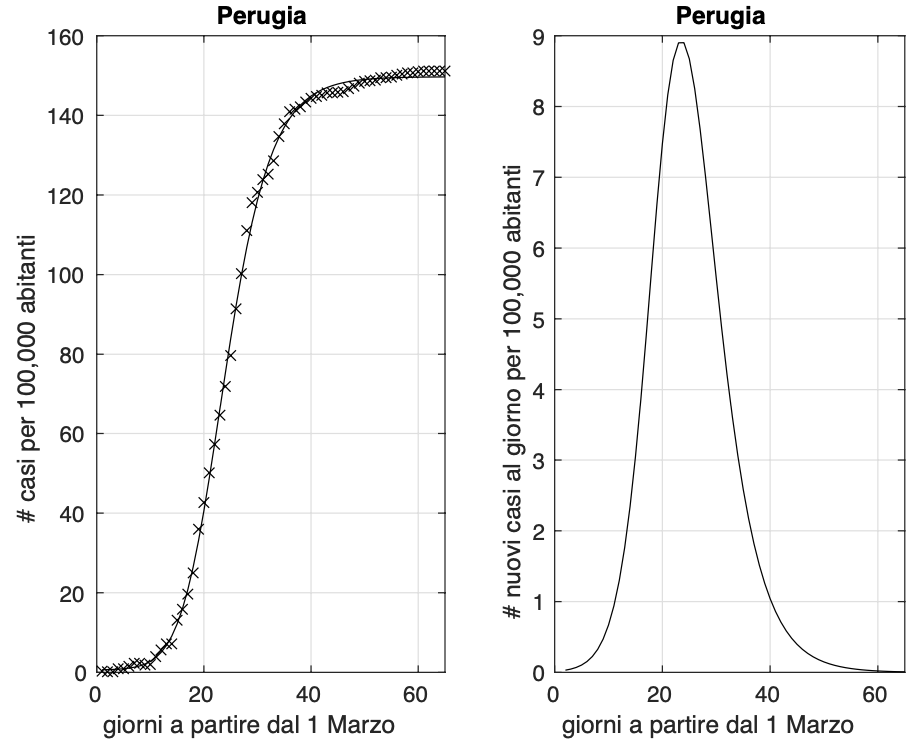
Figura 5. Sequenza del numero dei contagiati osservati nella provincia di Perugia. Il miglior fit con un modello logistico generalizzato è sovrapposto ai dati.
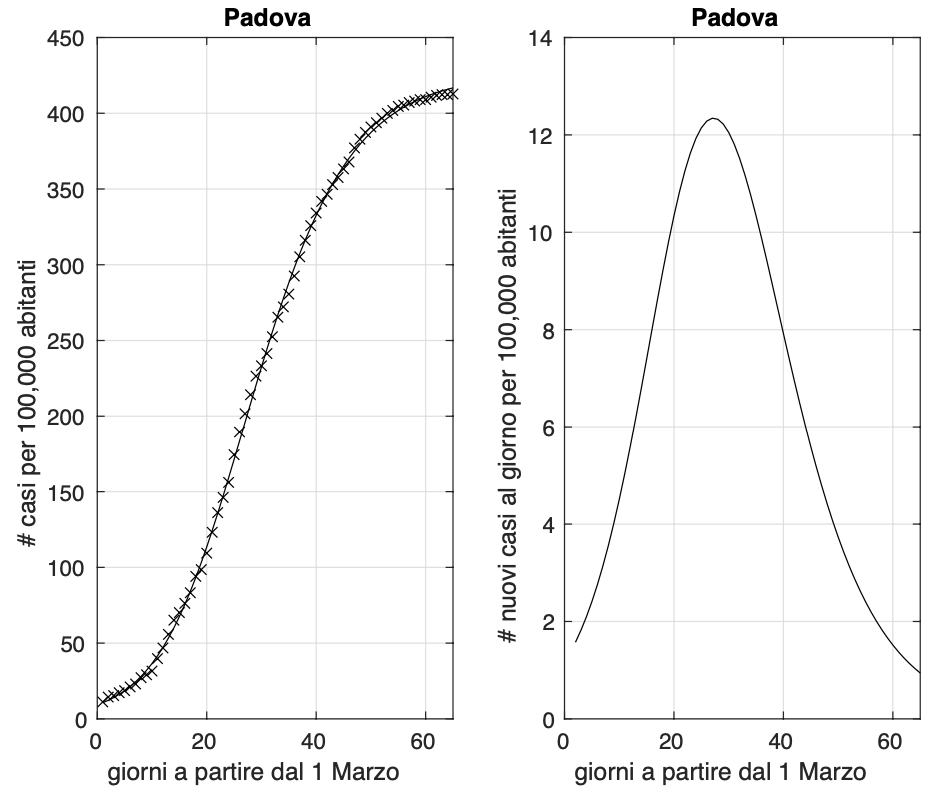
Figura 6. Sequenza del numero dei contagiati osservati nella provincia di Padova. Il miglior fit con un modello logistico generalizzato è sovrapposto ai dati.
Putroppo a livello regionale, Lombardia e soprattutto Piemonte, sono ancora in una fase di grande attività, come si può osservare nelle figure 7 e 8. Osservate speciali quindi queste due regioni nell’attuale “fase due” appena iniziata.
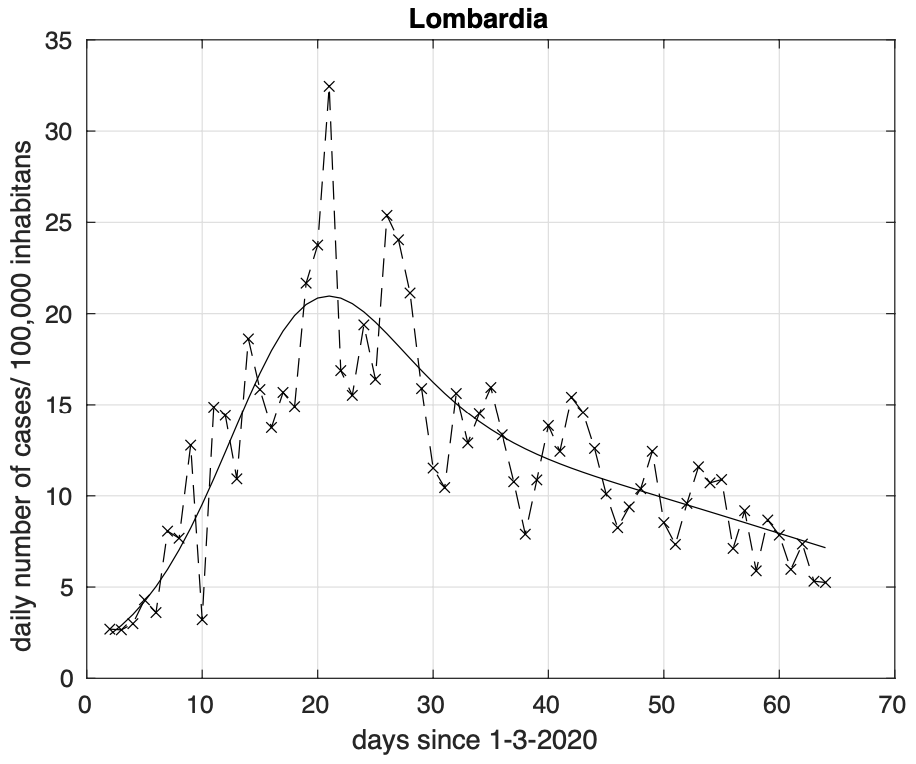
Figura 7. Sequenza del numero giornaliero di contagiati osservati in Lombardia. Il miglior fit con un modello logistico generalizzato (derivata) è sovrapposto ai dati.
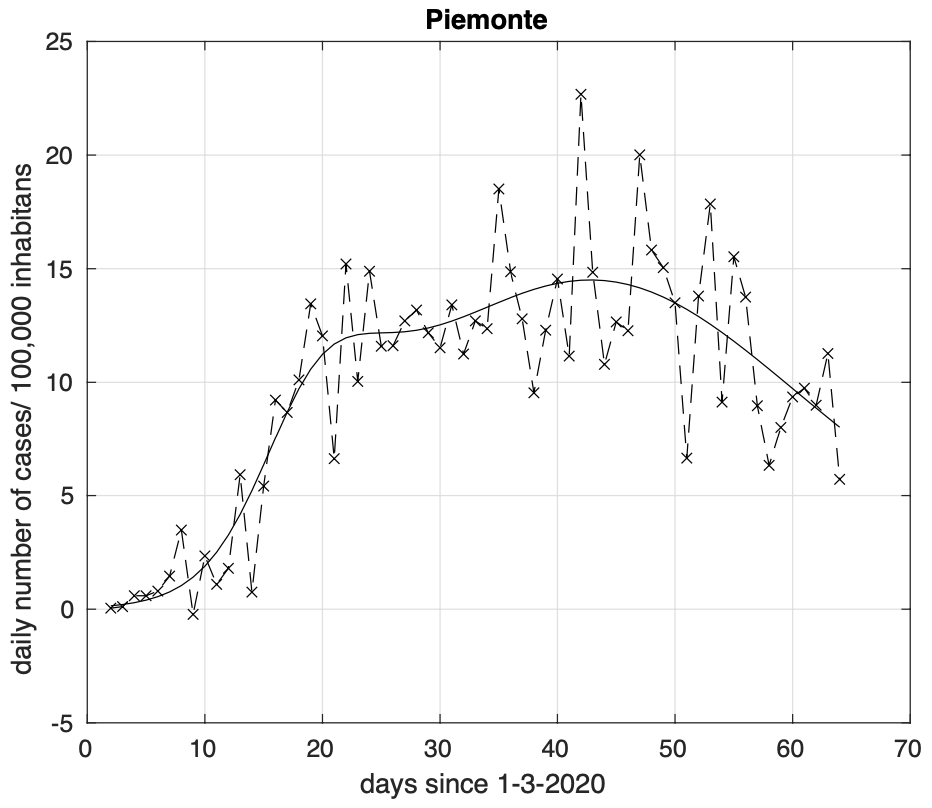
Figura 8. Sequenza del numero giornaliero di contagiati osservati in Piemonte. Il miglior fit con un modello logistico generalizzato (derivata) è sovrapposto ai dati.
L’invito per tutti è comunque quello di cercare di ridurre al minimo il rischio di contagiare ed essere contagiati, in primo luogo usando mascherina e guanti quando ci si trova in luoghi pubblici, mantenendo una debita distanza dalle altre persone. Abbiamo ottenuto un effetto macroscopico tramite il comportamento individuale di tutti, insieme, come un applauso “in fase” alla fine di un concerto. Non dobbiamo assolutamente vanificare lo sforzo profuso. A causa del periodo di incubazione della malattia e del tempo tra l’insorgenza dei primi sintomi e la diagnosi tramite test col tampone, abbiamo il tempo di una, due settimane per vedere gli effetti eventuali dell’introduzione di questa fase nella diffusione dell’epidemia. Se variamo di poco il nostro comportamento in relazione al rischio di contagio, ci aspettiamo che gli effetti siano nulli o contenuti. Questo ci permetterà di evitare un nuovo “lockdown”, le cui conseguenze negative sotto diversi aspetti sono evidenti a tutti.
Nota
In questo documento sono descritti i risultati relativi all’analisi per tutte le province e re- gioni italiane. I dati utilizzati sono quelli aggiornati alle 18 del 4 Maggio 2020 e sono stati scaricati dai siti https://github.com/pcm-dpc/COVID-19/tree/master/dati-province e https://github.com/pcm-dpc/COVID-19/tree/master/dati-regioni. I risultati sostituiscono o integrano quelli nel documento del 30 aprile. Valgono le stesse considerazioni generali del documento del 30 aprile. Alcuni chiarimenti possono essere trovati nella Nota Metodologica. I risultati di tutte le province possono essere scaricati qui.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
Analisi dei dati epidemiologici del coronavirus in Italia (al 30 aprile)
- 7330 letture
L’analisi delle sequenze temporali della frazione dei contagiati osservati rispetto alla popolazione della provincia rivela che 106 delle 107 province presentano una diminuzione del tasso di crescita. Manca all’appello solo la provincia di Asti (vedi figura 1).
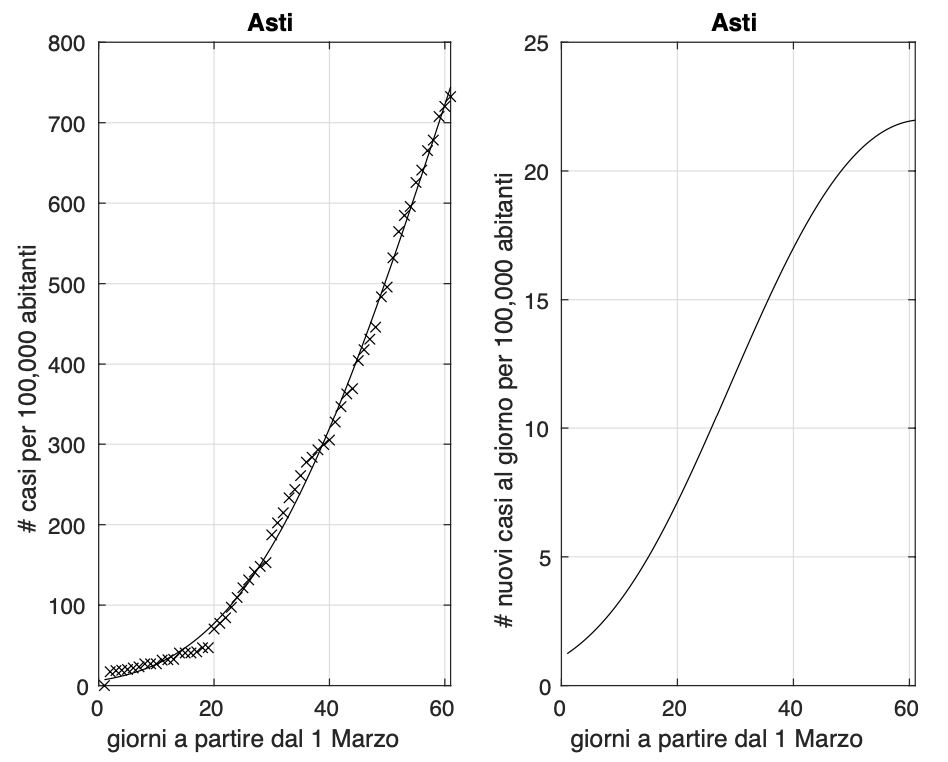
Figure 1. Sequenza del numero dei contagiati osservati nella provincia di Asti. Il miglior fit con un modello logistico generalizzato è sovrapposto ai dati.
Questo è in linea col fatto che la regione che si trova più arretrata rispetto alle altre nell’evoluzione dell’epidemia è il Piemonte, come mostrato in figura 2.

Figure 2. Sequenza del numero giornaliero di contagiati osservati nel Piemonte. Il miglior fit con un modello logistico generalizzato (derivata) è sovrapposto ai dati.
Dalla parte opposta abbiamo l’Umbria che è la regione più avanti nell’evoluzione dell’epidemia (vedi figura 3), pur avendo iniziato dopo nel tempo, per esempio rispetto alla Lombardia (vedi figura 4).
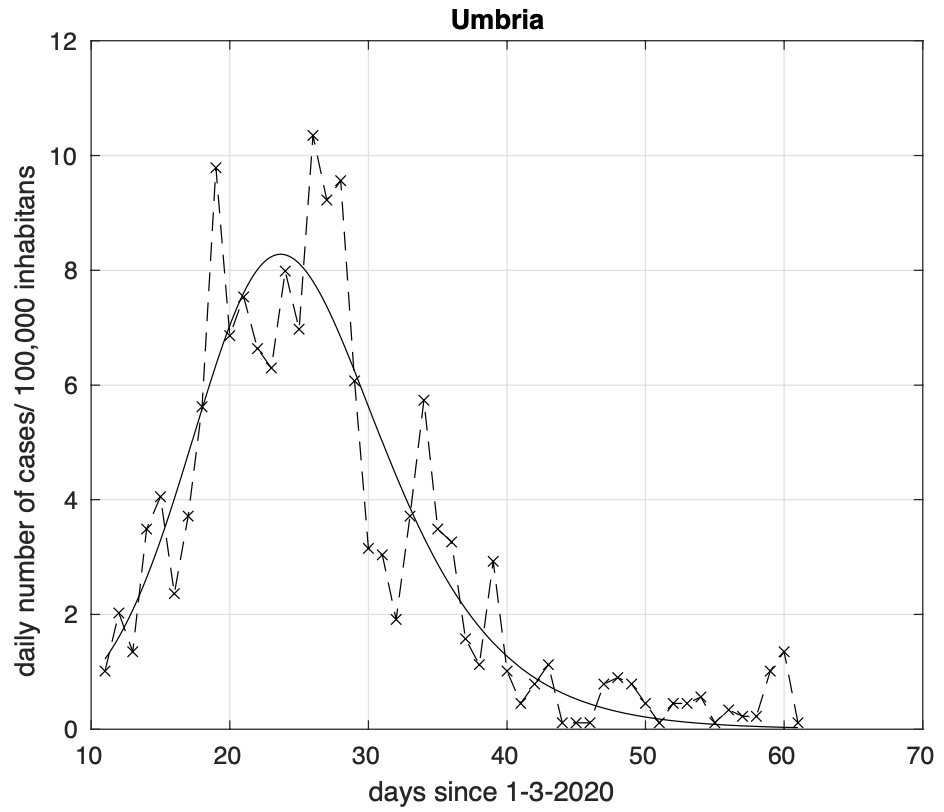
Figure 3. Sequenza del numero giornaliero di contagiati osservati in Umbria. Il miglior fit con un modello logistico generalizzato (derivata) è sovrapposto ai dati.
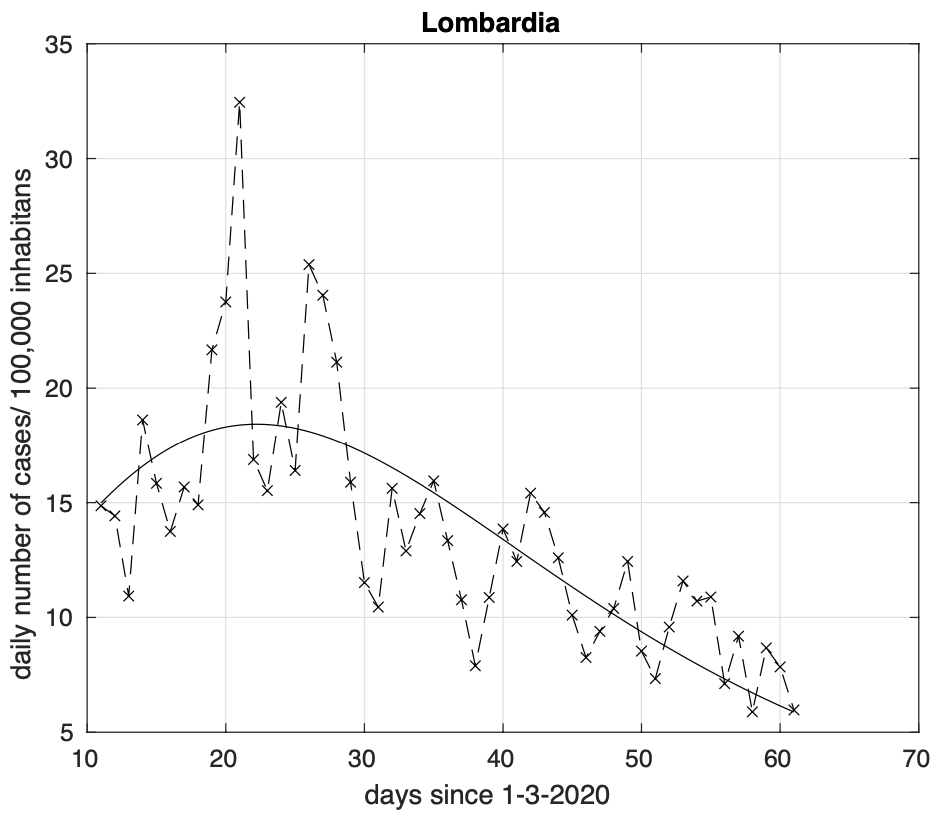
Figure 4. Sequenza del numero giornaliero di contagiati osservati nella Lombardia. Il miglior fit con un modello logistico generalizzato (derivata) è sovrapposto ai dati.
I risultati di tutte le regioni possono essere scaricati qui. Nelle figure precedenti, alle curve del numero di nuovi contagiati osservati giornalmente, sono stati sovrapposti i fit con il modello logistico generalizzato. Per ciascuna regione, abbiamo calcolato il valore massimo del modello ed il suo valore finale. Sulla base di queste due grandezze, abbiamo effettuato il clustering gerarchico (vedi nota metodologica), che permette di raggruppare le 21 regioni in gruppi in modo che la variabilità delle due grandezze considerate all’interno dei gruppi sia (localmente) minimizzata.
In figura 5 viene rappresentato il dendrogramma ottenuto tramite questa analisi. Si ha chiara evidenza della presenza di quattro gruppi, composti rispettivamente da:
- Piemonte, Lombardia, Liguria e Trento;
- Emilia Romagna, Marche, Veneto e Bolzano;
- Abruzzo, Basilicata, Calabria, Campania, Friuli Venezia Giulia, Lazio, Molise, Puglia, Sardegna, Sicilia, Toscana ed Umbria;
- Valle D'Aosta.
Le regioni del primo gruppo sono caratterizzate da grandi valori di entrambi le grandezze considerate.
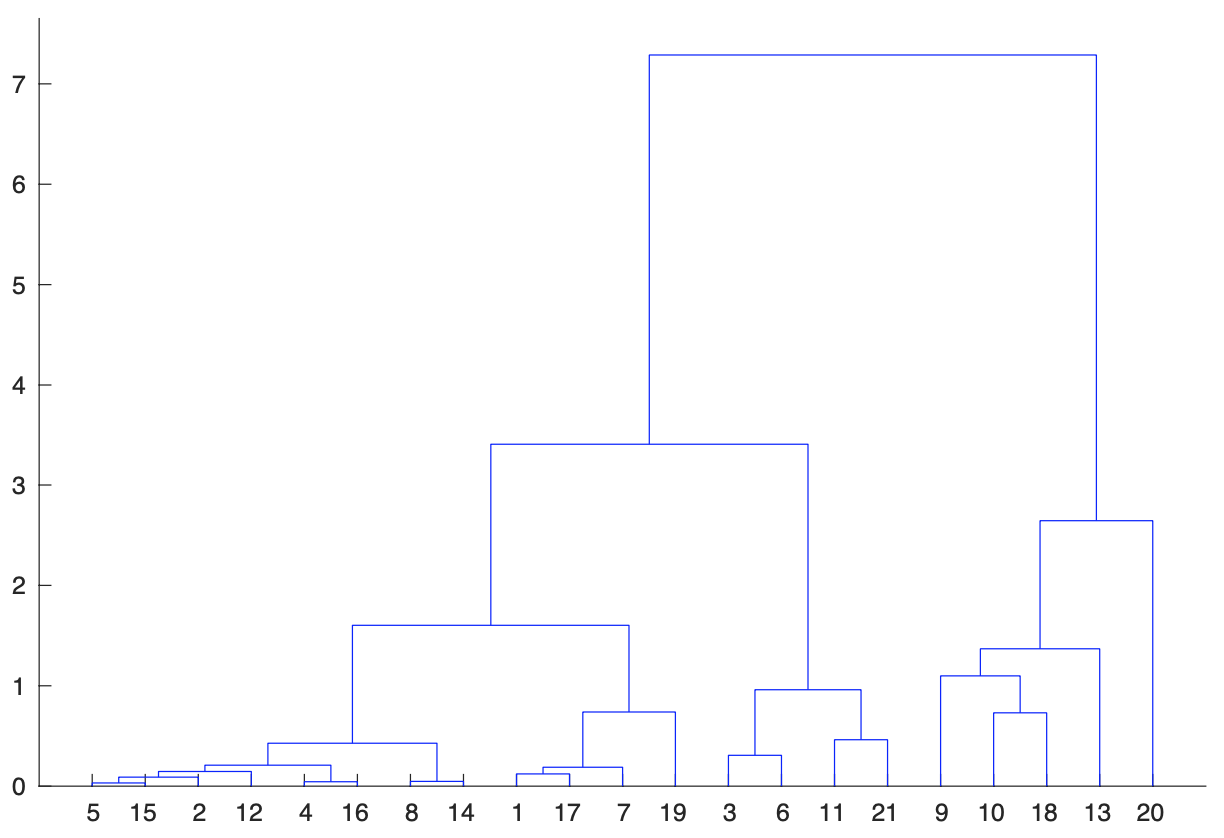
Figure 5. Dendrogramma ottenuto tramite il clustering gerarchico a partire dai dati per ciascuna regione del valore massimo e di quello finale del modello logistico generalizzato usato nel fit alle curve del numero giornaliero dei contagiati osservati.
Questi valori scendono passando dapprima al secondo gruppo e quindi al terzo. Le grandezze sono intuitivamente legate alla diffusione massima ed attuale dell’epidemia. Nel primo gruppo ci sono quindi le regioni che hanno subito una gran diffusione dell’epidemia che si trova ancora in una fase di rilevante attività. Nel secondo gruppo si è avuta una grande attività, ma ci si trova in una fase più avanzata dell’epidemia rispetto alle regioni del primo gruppo. Nel terzo gruppo si trovano le regioni che hanno avuto una diffusione ancora più bassa e che si trovano attualmente in una fase molto avanzata dell’epidemia. Infine, nell'ultimo gruppo c'e' la Valle D'Aosta che ha avuto una grande diffusione dell'epidemia, ma che si trova ora in una fase avanzata.
Note
In questo documento sono descritti i risultati relativi all’analisi per tutte le province e re- gioni italiane. I dati utilizzati sono quelli aggiornati alle 18 del 30 Aprile 2020 e sono stati scaricati dai siti https://github.com/pcm-dpc/COVID-19/tree/master/dati-province e https://github.com/pcm-dpc/COVID-19/tree/master/dati-regioni. I risultati sostituiscono o integrano quelli nel documento del 20 aprile.
Valgono le stesse considerazioni generali del documento del 20 aprile. Alcuni chiarimenti possono essere trovati nella Nota Metodologica. I risultati di tutte le province possono essere scaricati qui. I risultati di tutte le regioni possono essere scaricati qui.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
Analisi dei dati epidemiologici del coronavirus in Italia (al 20 aprile)
- 8055 letture
L’analisi delle sequenze temporali della frazione dei contagiati osservati rispetto alla popolazione della provincia rivela che 105 delle 107 province presentano una diminuzione del tasso di crescita. Mancano all’appello le province di Brindisi e Novara. I risultati di tutte le province possono essere scaricati qui. La regione che si trova più arretrata rispetto alle altre nell’evoluzione dell’epidemia è il Piemonte, come mostrato per esempio in figura 1 per la provincia di Asti.
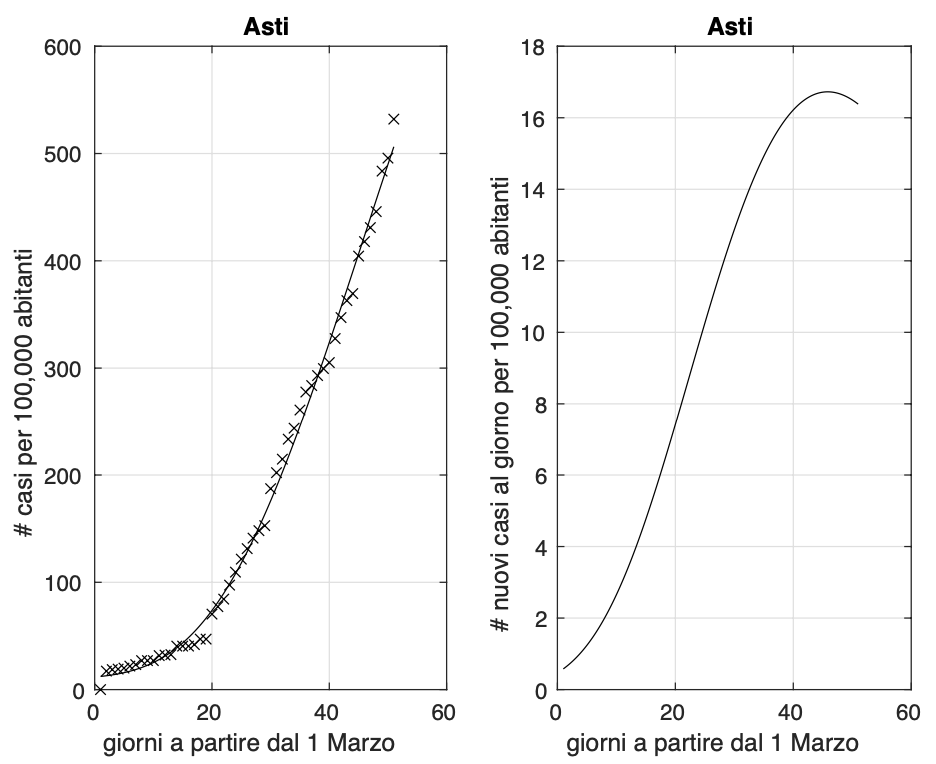
Figura 1. Sequenza del numero dei contagiati osservati nella provincia di Asti. Il miglior fit con un modello logistico generalizzato è sovrapposto ai dati.
Come per il 15 aprile, anche oggi buone notizie invece dal versante opposto. Ci sono infatti 19 province che oggi non registrano nuovi casi. A parte Aosta, le altre 18 sono tutte al centro o al sud. Naturalmente, bisogna sempre aspettare che il dato si consolidi nel tempo. Comunque, di queste 19, sono 10 quelle per cui questo si verifica per due giorni consecutivi e 6 quelle per almeno tre giorni. Quattro di queste sei, Agrigento, Caltanisetta, Ragusa e Trapani sono per cinque giorni a tasso zero, mentre sono sette i giorni per Sud Sardegna e nove per Crotone (vedi figura 2).
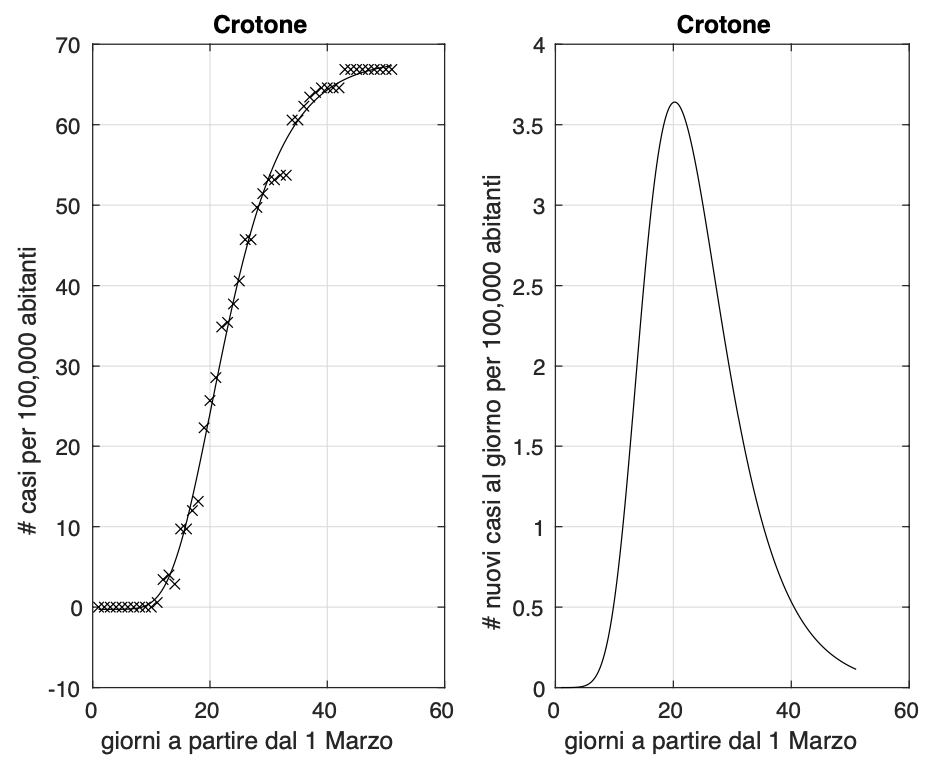
Figura 2. Sequenza del numero dei contagiati osservati nella provincia di Crotone. Il miglior fit con un modello logistico generalizzato è sovrapposto ai dati.
Alla luce di questi dati, abbiamo studiato alcune caratteristiche dell’evoluzione spaziale dell’epidemia di coronavirus in Italia.
Abbiamo dapprima preso Bergamo come punto di riferimento per la diffusione dell’epidemia. Fissato un giorno qualsiasi, abbiamo considerato i dati del numero di contagiati osservati in ciascun capoluogo di provincia fino a quel giorno. Per ciascuna capoluogo, abbiamo calcolato la sua distanza da Bergamo. Come distanza abbiamo scelto la lunghezza del cammino più breve, lungo la superficie di una sfera col raggio pari a quello terrestre (6.371 km), tra i due punti corrispondenti al capoluogo ed a Bergamo. Per il giorno considerato abbiamo quindi per ogni capoluogo la sua distanza da Bergamo e il numero di contagiati osservati al suo interno fino a quel giorno. Possiamo quindi calcolare la distanza media da Bergamo per quel giorno dei punti (capoluoghi) dove sono stati registrati casi di coronavirus fino ad allora. La media è di tipo pesato con i pesi proporzionali al numero di casi registrati per ciascun capoluogo fino a quel giorno. Come usualmente fatto nello studio del fenomeno della diffusione classica di particelle, la distanza media è calcolata prendendo la radice quadrata della media pesata del quadrato della distanza citata. Osserviamo che questa analisi non si occupa di studiare la diffusione dell’epidemia lungo particolari direzioni, ma considera tutte le direzioni assieme. In figura 3 mostriamo come varia la distanza media considerata al variare del tempo. Dal grafico vediamo che, a parte delle fluttuazioni di nessun significato, questa distanza aumenta nel tempo, per poi stabilizzarsi all’inizio di aprile.
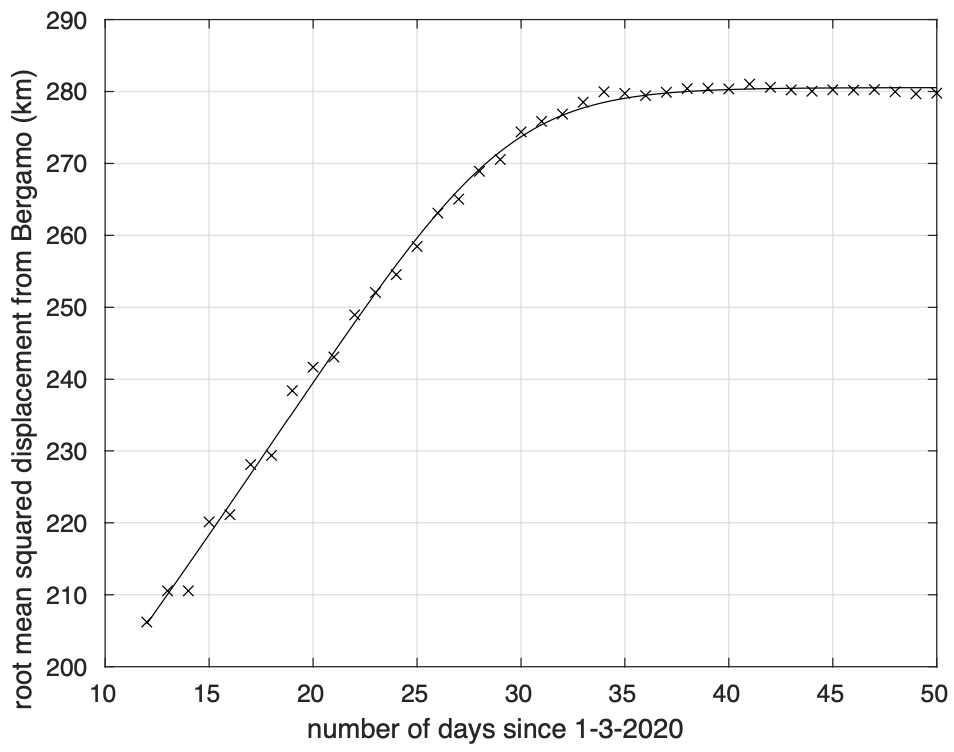
Figura 3. Andamento nel tempo della “distanza media” (in km) da Bergamo, origine della diffusione del coronavirus in Italia, dei punti del territorio italiano interessati dall’epidemia. Il miglior fit con un modello logistico generalizzato è sovrapposto ai dati calcolati.
Successivamente abbiamo calcolato la distribuzione spaziale al variare della latitudine del numero totale di contagiati osservati in Italia al 19 aprile, mostrata in figura 4. Come si vede dalla figura, l’epidemia ha interessato in maniera preponderante il nord, per poi diminuire in media spostandoci in direzione del sud.
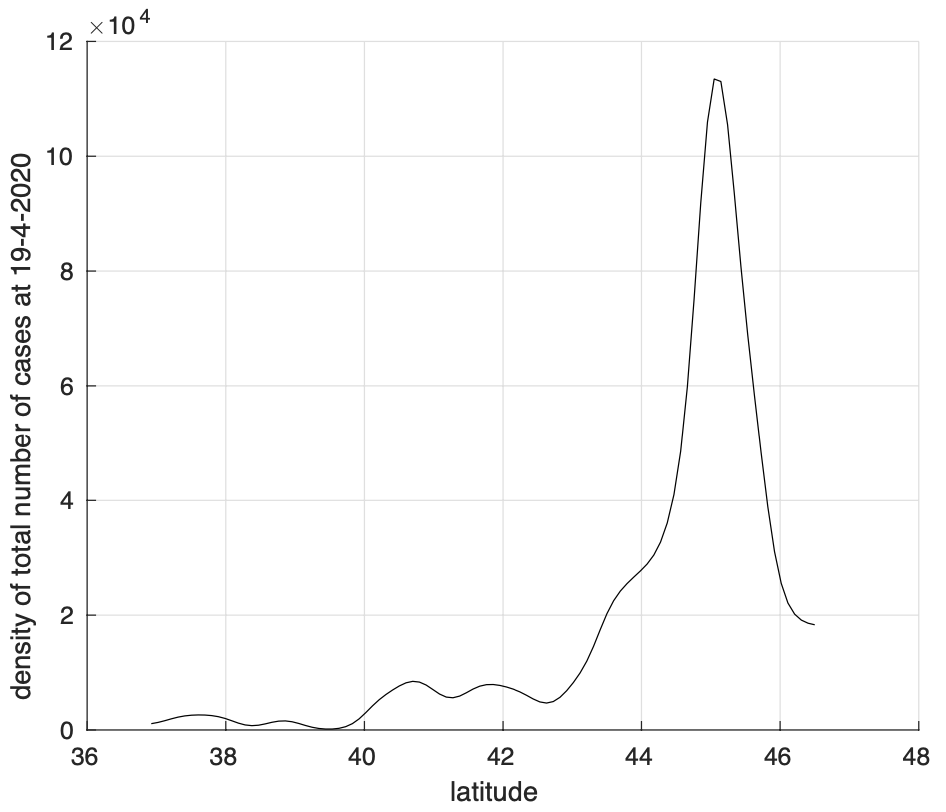
Figura 4. Distribuzione spaziale del numero di contagiati osservati in Italia al 19 aprile al variare della latitudine.
Nella figura 5 viene invece illustrata l’evoluzione temporale dell’epidemia nelle tre zone geografiche dell’Italia: il nord (latitudine al di sopra di +44 gradi, che corrisponde approssimativamente al punto più a sud dell’Emilia Romagna), il centro (latitudine tra +41 gradi, che corrisponde approssimativamente al punto più a nord della Sardegna, e +44 gradi) ed il sud (latitudine inferiore a +41 gradi). Anche qui osserviamo una diminuzione notevole del coinvolgimento spostandoci da nord verso sud.
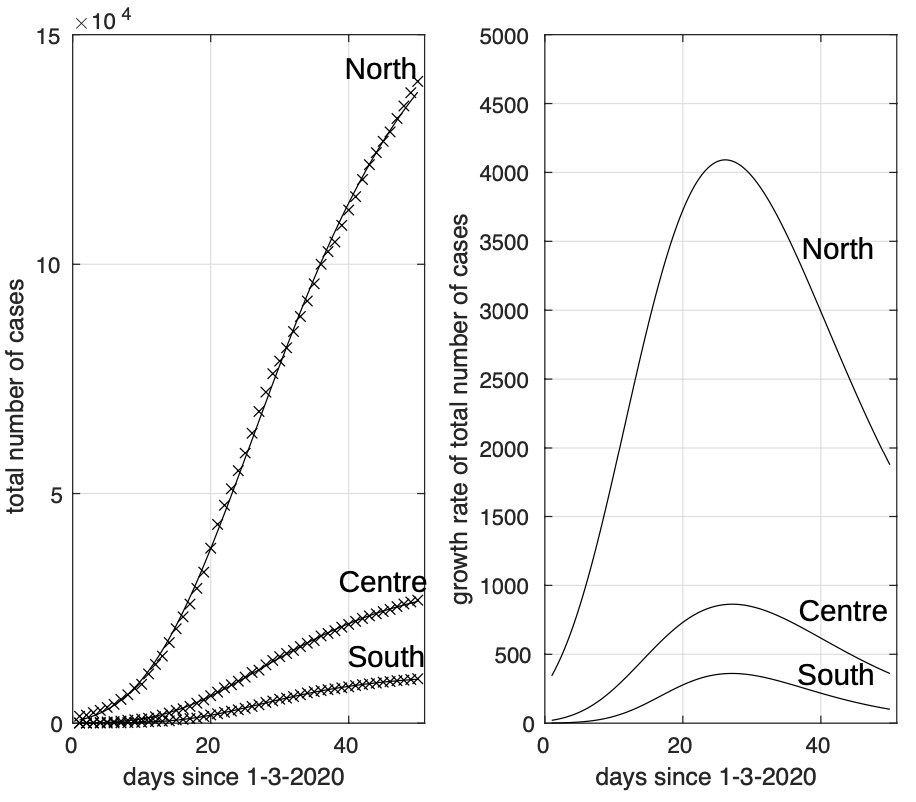
Figura 5. Sequenza del numero dei contagiati osservati in Italia (a sinistra) al nord, al centro e al sud. Il miglior fit con un modello logistico generalizzato è sovrapposto ai dati. A destra sono mostrati i relativi tassi di crescita.
Nota
In questo documento sono descritti i risultati relativi all’analisi per tutte le province italiane. I dati utilizzati sono quelli aggiornati alle 18 del 20 Aprile 2020 e sono stati scaricati dal sito https://github.com/pcm-dpc/COVID19/tree/master/dati-province. I risultati sosti- tuiscono o integrano quelli nel documento del 15 Aprile.
Valgono le stesse considerazioni generali del documento del 15 Aprile. Alcuni chiarimenti possono essere trovati nella Nota Metodologica. I risultati di tutte le province possono essere scaricati qui.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
Analisi dei dati epidemiologici del coronavirus in Italia (al 15 aprile)
- 6816 letture
L’analisi delle sequenze temporali della frazione dei contagiati osservati rispetto alla popolazione della provincia rivela che 102 delle 107 province presentano una diminuzione del tasso di crescita. Mancano all’appello le province di Brindisi, Genova, Barletta-Andria-Trani, Novara e Cagliari. I risultati di tutte le province possono essere scaricati qui.
Ci sono invece 11 province che oggi non registrano nuovi casi: Chieti, Matera, Crotone, Vibo Valentia, Benevento, Viterbo, Isernia, Nuoro, Sud Sardegna, Grosseto e Terni. Tra queste, quelle per cui questo accade da alcuni giorni sono Terni, Crotone, Vibo Valentia e Nuoro. Come già osservato il 10 aprile, Perugia è comunque la provincia dove l’evoluzione dell’epidemia ha mostrato prima che per altre di essere vicina alla fase conclusiva. Infatti, pur essendo oggi stato registrato a Perugia un nuovo caso, il numero totale di casi per questa provincia è molto più alto di quelli delle undici province oggi a zero nuovi contagi.
Possiamo dire che l’Umbria è la regione che per prima si avvia verso la fine dell’epidemia (vedi le figure 1 e 2). La raccomandazione di continuare a limitare al minimo il rischio di contagio è d’obbligo. Per quanto riguarda le discrepanze osservate tra i dati e il modello teorico nell’ultima parte dell’intervallo temporale, osservate di recente per diverse province e già sottolineate il 10 aprile, verrà pubblicato a breve un documento specifico che coinvolge alcuni aspetti generali riguardanti i test con i tamponi per individuare gli individui infettati.
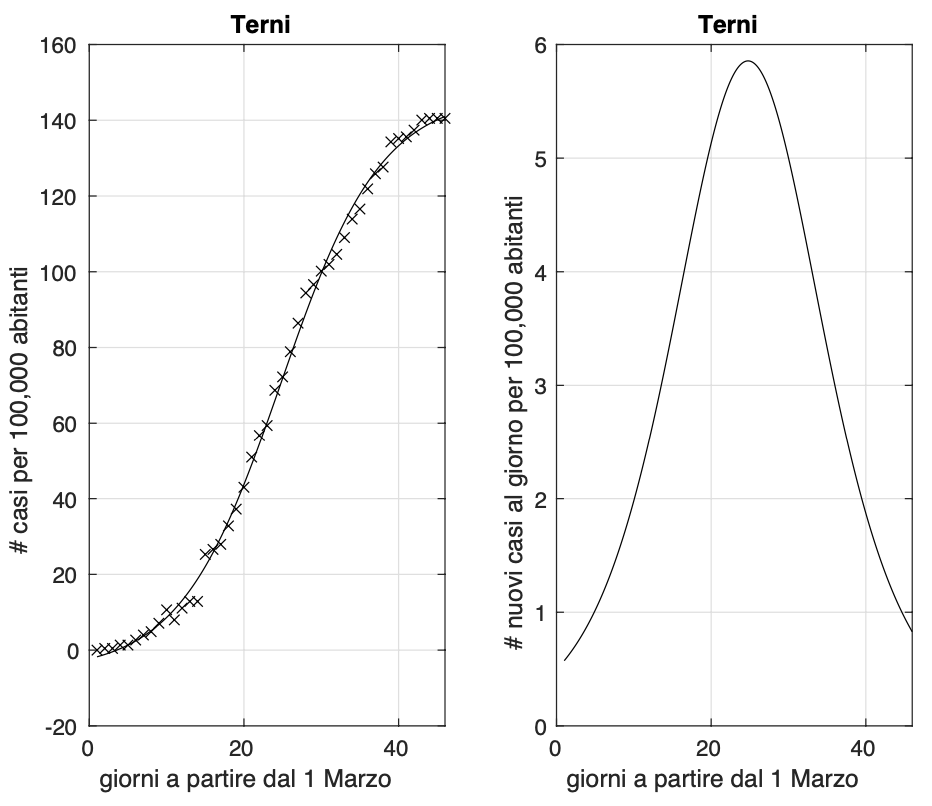
Figura 1. Sequenza del numero dei contagiati osservati nella provincia di Terni. Il miglior fit con un modello logistico è sovrapposto ai dati.
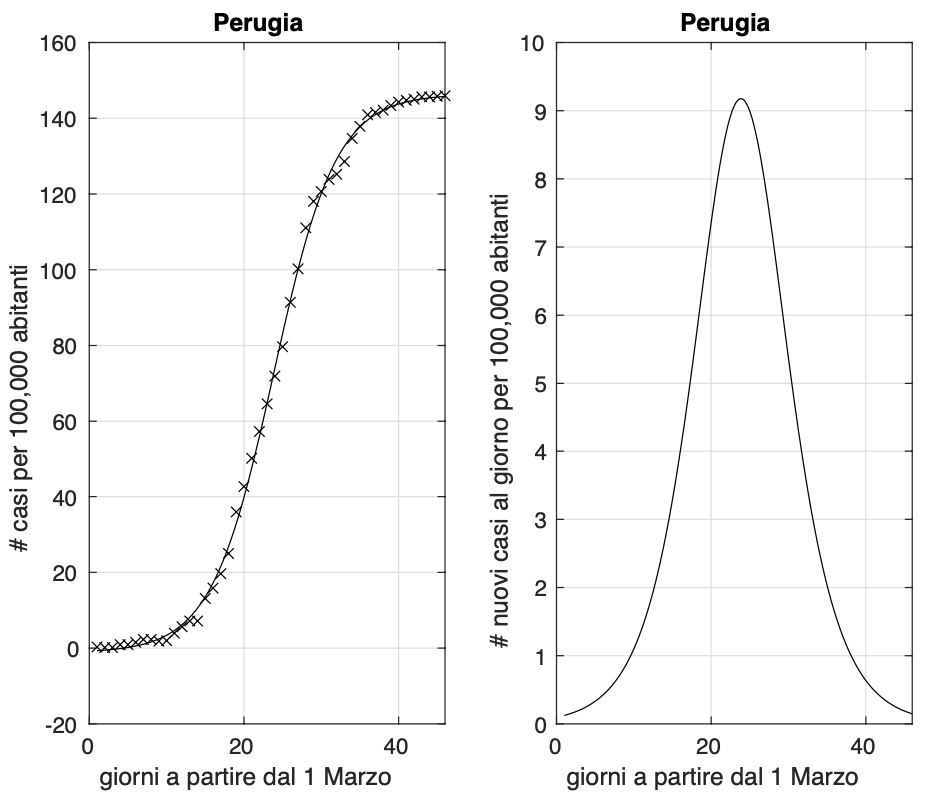
Figura 2. Sequenza del numero dei contagiati osservati nella provincia di Perugia. Il miglior fit con un modello logistico è sovrapposto ai dati.
Note
In questo documento sono descritti i risultati relativi all’analisi per tutte le province italiane. I dati utilizzati sono quelli aggiornati alle 18 del 15 aprile 2020 e sono stati scaricati dal sito https://github.com/pcm-dpc/COVID-19/tree/master/dati-province. I risultati sostituiscono o integrano quelli nel documento del 10 aprile. Valgono le stesse considerazioni generali del documento del 10 aprile. Alcuni chiarimenti possono essere trovati nella Nota metodologica. I risultati di tutte le province possono essere scaricati qui.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
Analisi dei dati epidemiologici del coronavirus in Italia (al 10 aprile)
- 8963 letture
L’analisi delle sequenze temporali della frazione dei contagiati osservati rispetto alla popolazione della provincia rivela che 98 delle 107 province presentano una diminuzione del tasso di crescita. Mancano all’appello le province di Oristano, Varese, Verbano-Cusio-Ossola, Brindisi, Genova, Imperia, Savona, La Spezia e Barletta-Andria-Trani. A parte le quattro province liguri, che il 5 aprile hanno visto innalzare il loro numero di contagiati osservati di centinaia di unità a causa di ritardi nell’esecuzione dei test e/o nella trasmissione dei loro risultati, sono rimaste solo altre 5 province mancanti. I risultati di tutte le province analizzate possono essere scaricati qui.
C’è una provincia che sembrerebbe poter a giorni raggiungere per prima la stabilizzazione del numero dei contagiati, quella di Perugia, come si può osservare dalla figura 1.
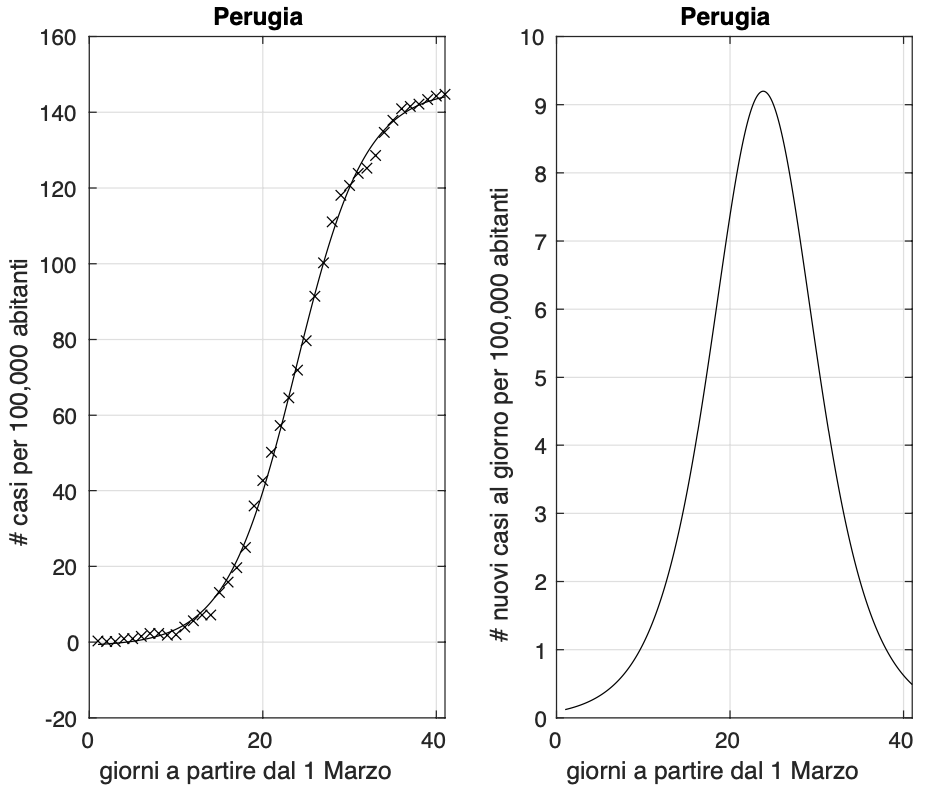
Figura 1. Sequenza del numero dei contagiati nella provincia di Perugia. Il miglior fit con un modello logistico è sovrapposto ai dati.
Naturalmente vedremo cosa succede nei prossimi giorni. Notiamo invece alcuni segni preoccupanti di eccesso di contagiati osservati rispetto al modello logistico negli ultimi giorni per 40 delle 98 province che hanno raggiunto il picco, come si osserva ad esempio in figura 2 per la provincia di Brescia.
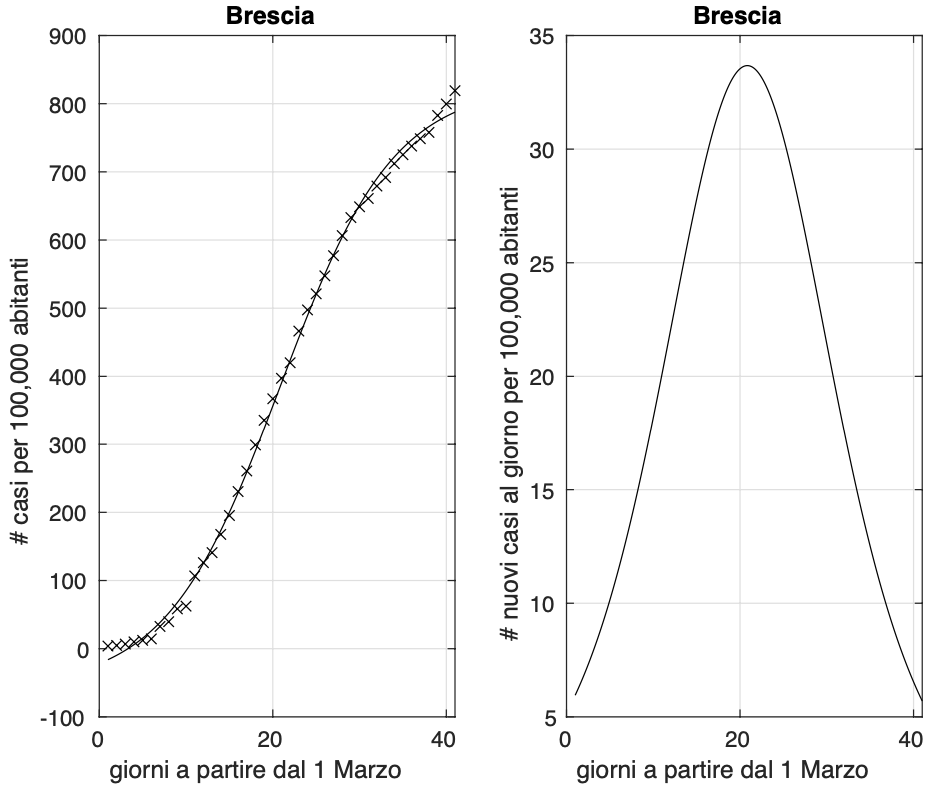
Figure 2. Sequenza del numero dei contagiati nella provincia di Brescia. Il miglior fit con un modello logistico è sovrapposto ai dati.
Speriamo che questo non rifletta un cambiamento reale della diffusione dell’epidemia indotto ad esempio da cambiamenti del nostro comportamento collettivo. Non sembra un effetto dovuto a variazioni degli schemi per l’individuazione dei soggetti a cui effettuare i test, come si pu`o osservare dalla figura 3.
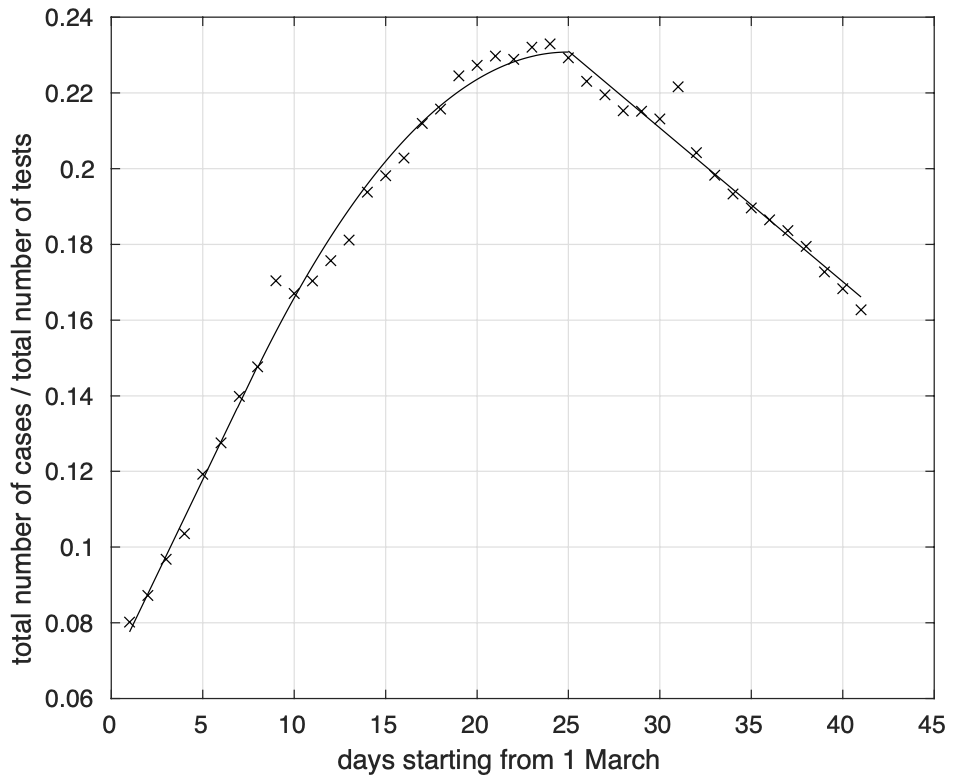
Figure 3. Andamento temporale del rapporto tra numero totale di contagiati osservati e numero totale di test effettuati.
Il grafico di questa figura rappresenta l’andamento nel tempo del rapporto tra numero totale di contagiati e numero totale di test effettuati e non si notano variazioni significative negli ultimi giorni verso la direzione indicata. Infatti, le deviazioni sotto il modello lineare osservate negli ultimi tre giorni, si interpretano probabilmente in termini di una piccola ma visibile variazione periodica settimanale, legata all'esecuzione dei test e alla trasmissione e registrazione dei loro risultati. La causa potrebbe invece essere la non adeguatezza del modello logistico per descrivere l’intera sequenza dei contagiati osservati. Vedremo cosa accade nei prossimi giorni ed in caso adotteremo un altro modello, per esempio quello di Gompertz (questo modello, come un altro da noi derivato a partire dal modello logistico, contiene un parametro addizionale che permette di controllare in modo indipendente la fase iniziale e quella finale). Il grafico di questa figura è comunque interessante. Infatti, possiamo notare che fino al 9 marzo, giorno di attuazione del decreto che istituiva la zona rossa in Lombardia, si ha un aumento lineare del rapporto considerato come appare dalla pendenza costante della curva. A partire dal 9 marzo si ha una progressiva diminuzione della pendenza della curva causata probabilmente dalla diminuzione dei contagi indotta dalle norme sulla restrizione della mobilità. Per via del tempo di incubazione del virus e del tempo per effettuare la diagnosi una volta che sono apparsi i sintomi, il massimo effetto si ha dopo due settimane dal 9 marzo, quasi in coincidenza col raggiungimento del picco del tasso dei contagiati osservati a livello nazionale il 26 marzo (vedi figura 4).
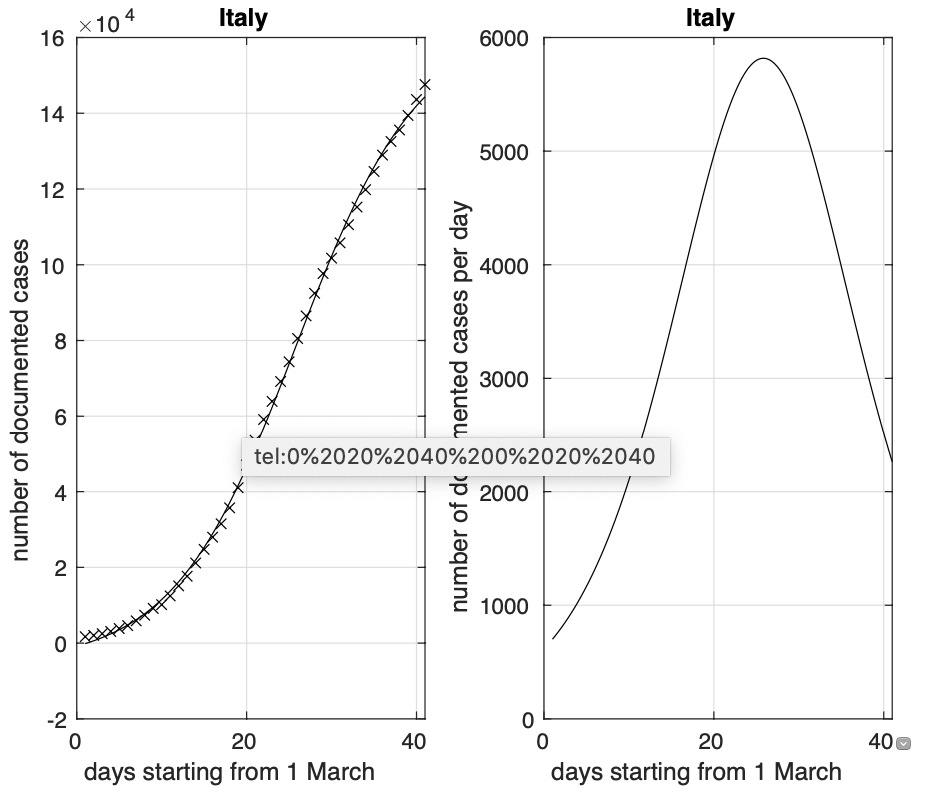
Figura 4. Sequenza del numero dei contagiati in Italia. Il miglior fit con un modello logistico è sovrapposto ai dati.
Cambiando argomento, possiamo essere contenti che anche l’Inghilterra abbia raggiunto il picco il 6 aprile, come di può vedere dalla figura 5.
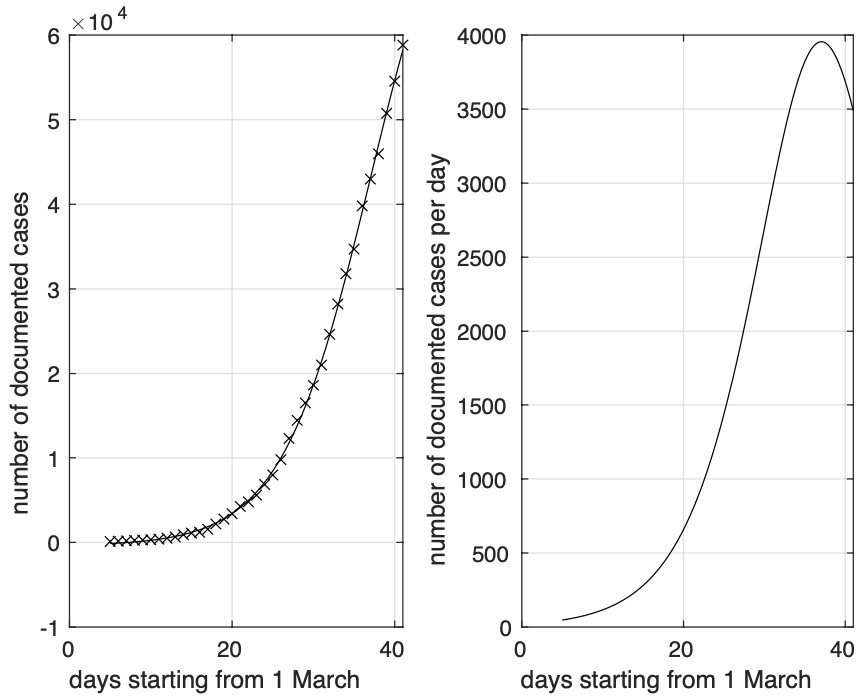
Figura 5. Sequenza del numero dei contagiati in Inghilterra. Il miglior fit con un modello logistico è sovrapposto ai dati.
Questo accade anche per Scozia, Irlanda del Nord e Galles il 4 e 5 aprile. Ricordiamo che il lockdown inglese ha avuto inizio il 24 marzo. Nel caso inglese quindi il picco viene raggiunto 12-14 giorni dopo l’inizio del lockdown. Per l’Italia questo avviene invece dopo 15-18 giorni dall’attuazione dei decreti dell’8 ed 11 marzo (9 e 12 marzo). Questo probabilmente dipende dal fatto che nel Regno Unito l’inizio del lockdown avviene in una fase antecedente della diffusione dell’epidemia rispetto all’Italia, come testimoniato dal tasso di crescita più basso di quello italiano.
Nota
In questo documento sono descritti i risultati relativi all’analisi per tutte le province italiane. I dati utilizzati sono quelli aggiornati alle 18 del 10 aprile 2020 e sono stati scaricati dal sito https://github.com/pcm-dpc/COVID-19/tree/master/dati-province. I risultati sosti- tuiscono o integrano quelli nel documento del 6 Aprile. Valgono le stesse considerazioni generali del documento del 6 Aprile. Alcuni chiarimenti possono essere trovati nella Nota metodologica. I risultati di tutte le province possono essere scaricati qui.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
Analisi dei dati epidemiologici del coronavirus in Italia (al 6 aprile)
- 9076 letture
L’analisi delle sequenze temporali della frazione dei contagiati osservati rispetto alla popolazione della provincia rivela che 94 delle 107 province presentano una diminuzione del tasso di crescita. Mancano all’appello tutte le province di ieri: Firenze, Napoli, Oristano, Avellino, Varese, Latina, Isernia, Brindisi, Genova, Imperia, Savona e La Spezia. Si è inoltre aggiunta la provincia di Barletta-Andria-Trani per la quale abbiamo lo stesso problema di ieri delle quattro province della Liguria. A parte queste ultime cinque province, i cui problemi sono di tipo sperimentale, notiamo una certa resistenza al superamento del picco nelle restanti otto province di Firenze, Napoli, Oristano, Avellino, Varese, Latina, Isernia e Brindisi. I risultati di tutte le province possono essere scaricati qui.
Di seguito alcune province con andamenti diversi: ancora in crescita, in rallentamento, in diminuzione. Nelle figure 1 e 2 rispettivamente le province di Latina e Varese dove la crescita dei nuovi casi ha ancora un andamento lineare. Per queste province le curve mostrano dapprima un salto (dovuto a problemi di ritardo nell'esecuzione dei testo o nella trasmissione dei risultati oppure all'esito di test eseguiti contemporaneamente su decine di pazienti in case di riposo, come avvenuto a Fondi il 20 marzo) e successivamente mostrano una crescita lineare, segno di un equilibrio tra nuovi casi e guariti e morti. Nella figura 3, la provincia di Firenze, dove la curva mostra segni iniziali di appiattimento. Nelle figure 4 e 5 le province di Crotone e Perugia dove invece si registra un rallentamento del tasso di crescita dei nuovi casi.
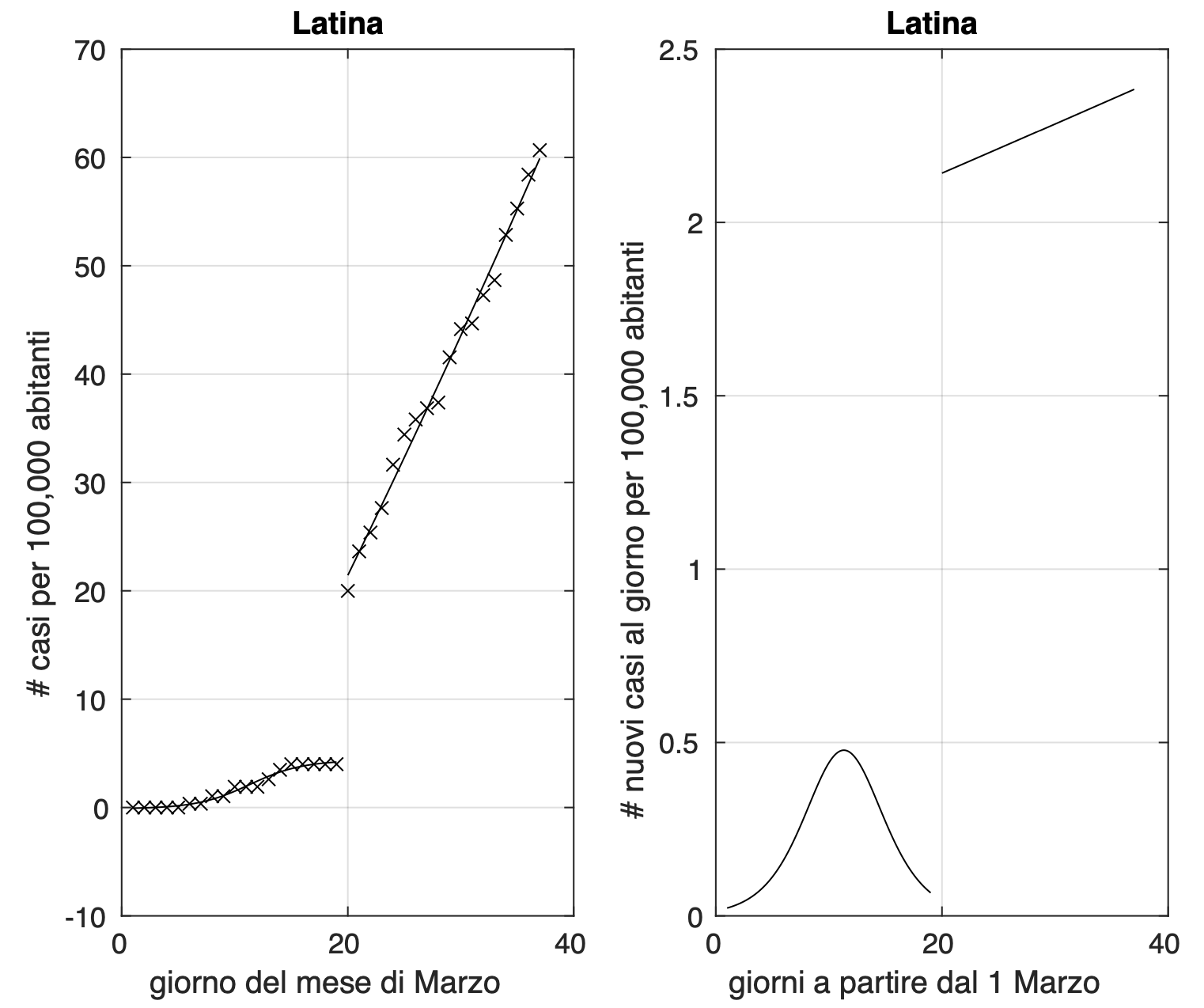
Figura 1. Sequenza del numero dei contagiati nella provincia di Latina. Il miglior fit con un modello logistico è sovrapposto ai dati.
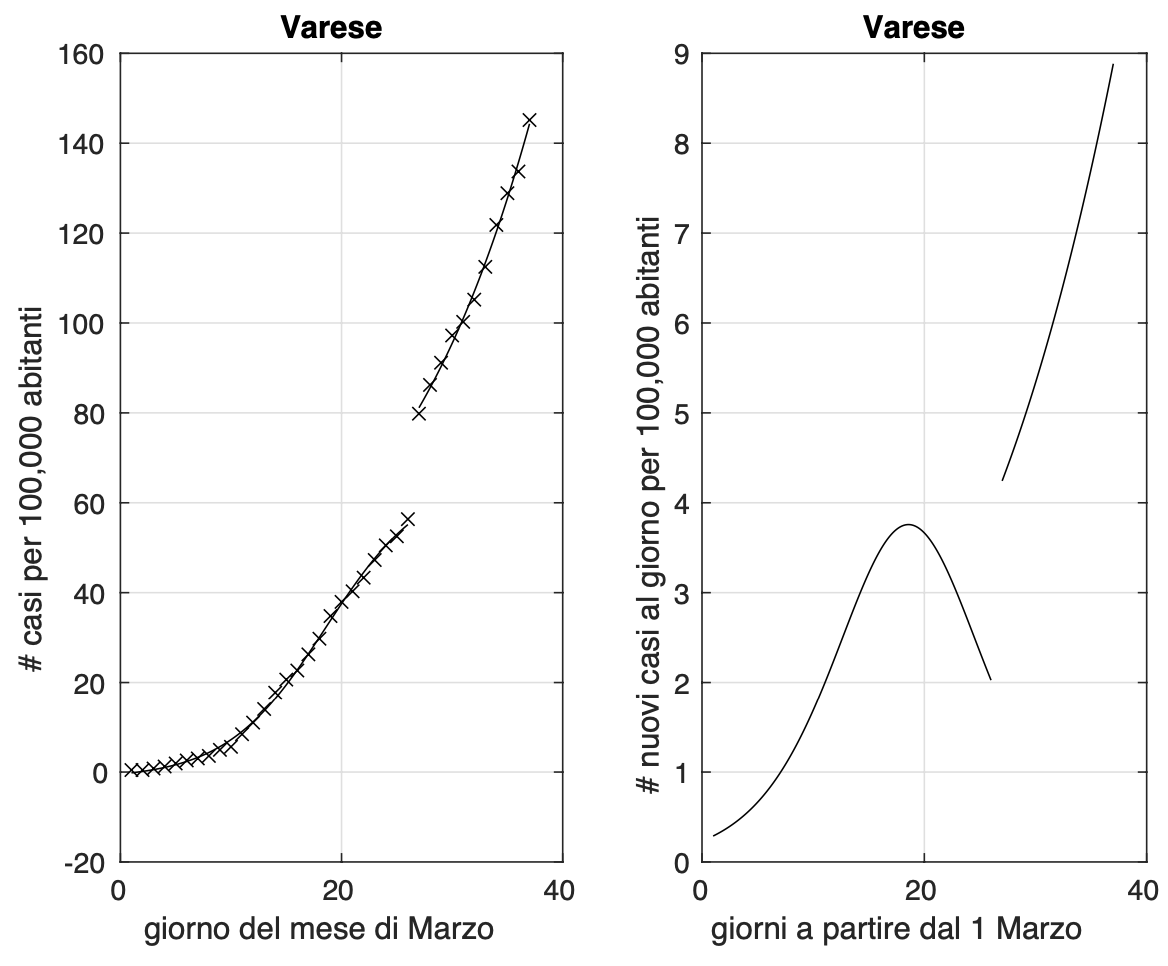
Figura 2. Sequenza del numero dei contagiati nella provincia di Varese. Il miglior fit con un modello logistico è sovrapposto ai dati.
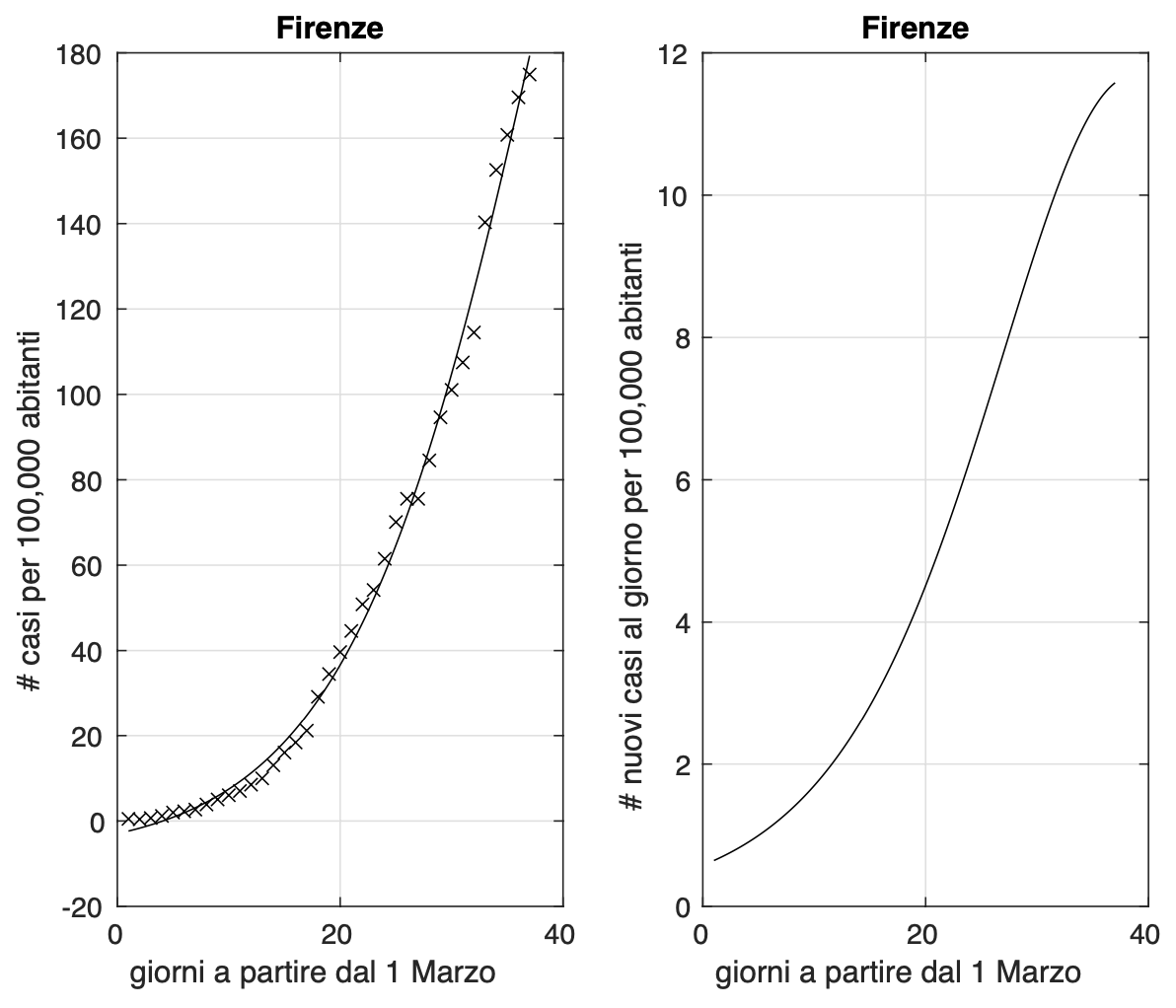
Figura 3. Sequenza del numero dei contagiati nella provincia di Firenze. Il miglior fit con un modello logistico è sovrapposto ai dati.
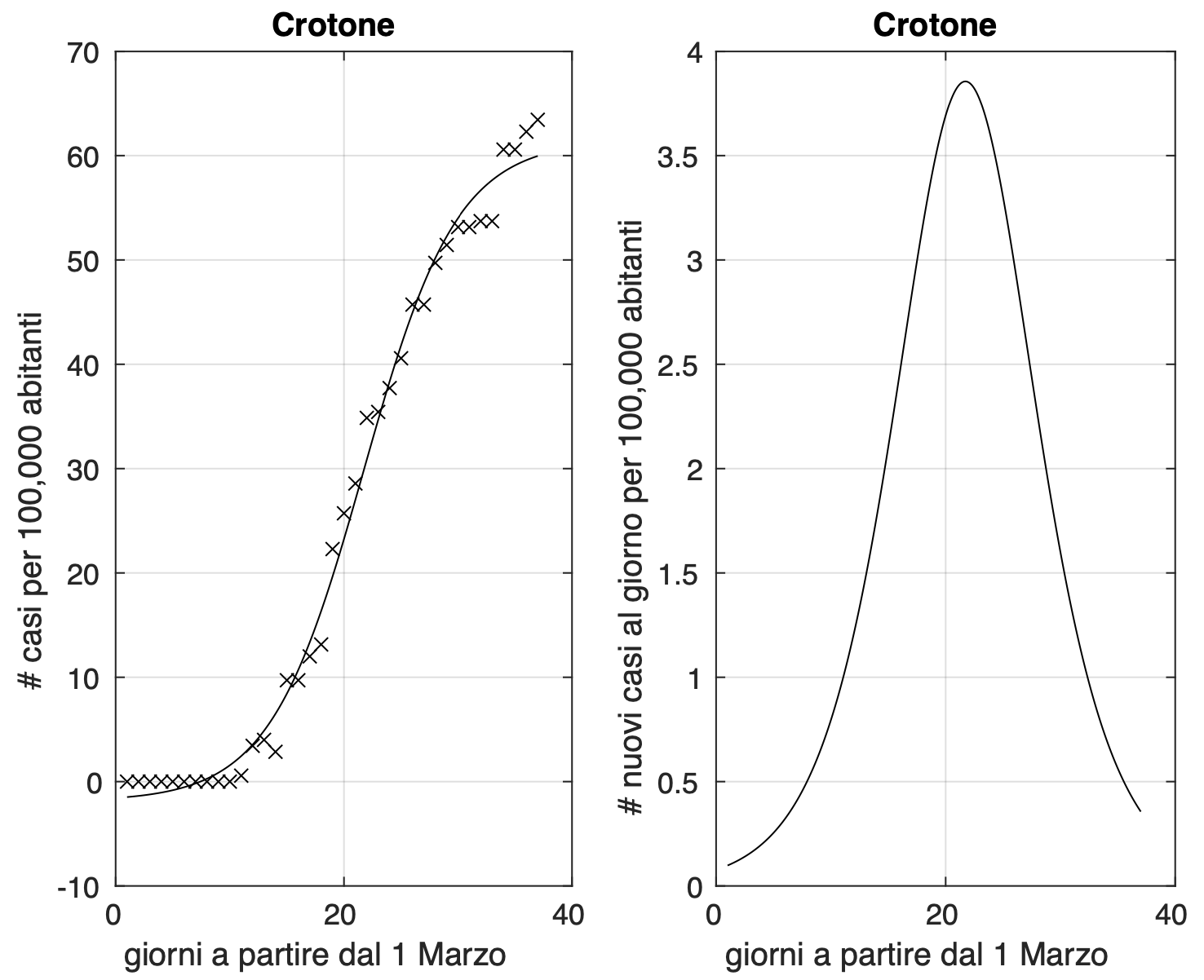
Figura 4. Sequenza del numero dei contagiati nella provincia di Crotone. Il miglior fit con un modello logistico è sovrapposto ai dati.
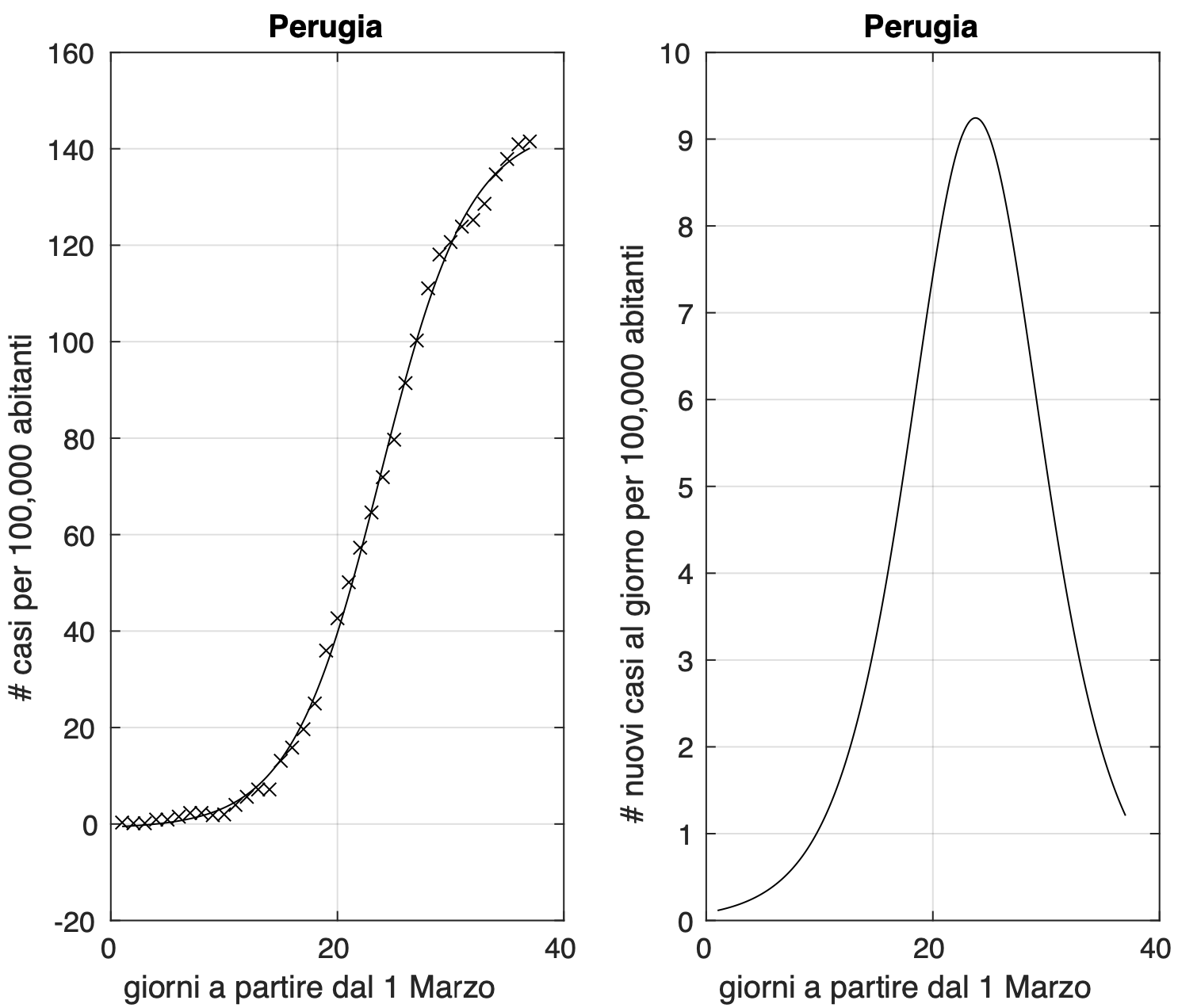
Figura 5. Sequenza del numero dei contagiati nella provincia di Perugia. Il miglior fit con un modello logistico è sovrapposto ai dati.
Nota
In questo documento sono descritti i risultati relativi all’analisi per tutte le province italiane. I dati utilizzati sono quelli aggiornati alle 18 del 6 aprile 2020 e sono stati scaricati dal sito https://github.com/pcm-dpc/COVID-19/tree/master/dati-province. I risultati sostituiscono o integrano quelli nel documento del 5 aprile. Valgono le stesse considerazioni generali del documento del 5 aprile. Alcuni chiarimenti possono essere trovati nella Nota metodologica. I risultati di tutte le province possono essere scaricati qui.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
Analisi dei dati epidemiologici del coronavirus in Italia (al 5 aprile)
- 8032 letture
L’analisi delle sequenze temporali della frazione dei contagiati osservati rispetto alla popolazione della provincia rivela che 95 delle 107 province presentano una diminuzione del tasso di crescita. Mancano all’appello le province di Firenze, Napoli, Oristano, Avellino, Varese, Latina, Isernia, Brindisi, Genova, Imperia, Savona e La Spezia. I risultati di tutte le province possono essere scaricati qui. Osserviamo che il numero di province che a oggi ha passato il picco è inferiore a quello del 2 aprile (96). Notiamo inoltre la presenza in questo gruppo di tutte le province della Ligura e che ciascuna di esse mostra un aumento notevole del numero totale di contagiati osservati rispetto al 2 aprile (vedi figura 1): la spiegazione non ha niente a che vedere con l’evoluzione dell’epidemia, basta notare che il 4 aprile per la Liguria c’erano più di 2.000 casi in via di definizione, mentre il 5 aprile essi sono poco più di 750. Prima che nei prossimi giorni qualcuno possa essere spaventato per un aumento dei casi in Lombardia, osserviamo che questa provincia ha a oggi più di 1.100 casi in via di definizione. Ci sono invece province che a breve potrebbero raggiungere valori trascurabili del numero di nuovi casi al giorno, come Crotone (vedi figura 2). Sebbene questo sia rassicurante, esortiamo tutti i residenti di questa provincia, o di altre nella stessa situazione, a continuare a seguire le norme come hanno sinora fatto e successivamente anche le prossime che verranno introdotte.
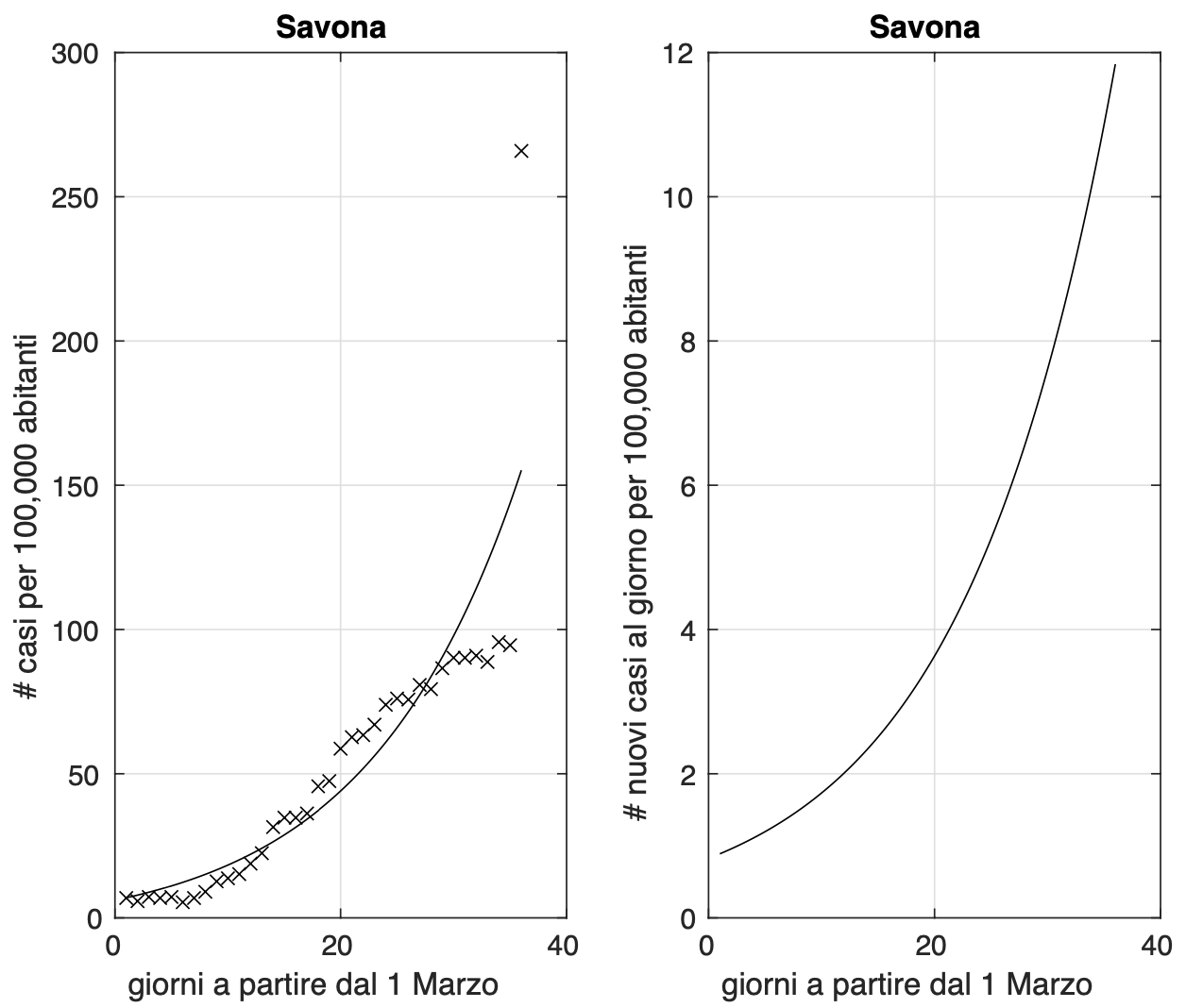
Figura 1. Sequenza del numero dei contagiati nella provincia di Savona. Il miglior fit con un modello logistico è sovrapposto ai dati.
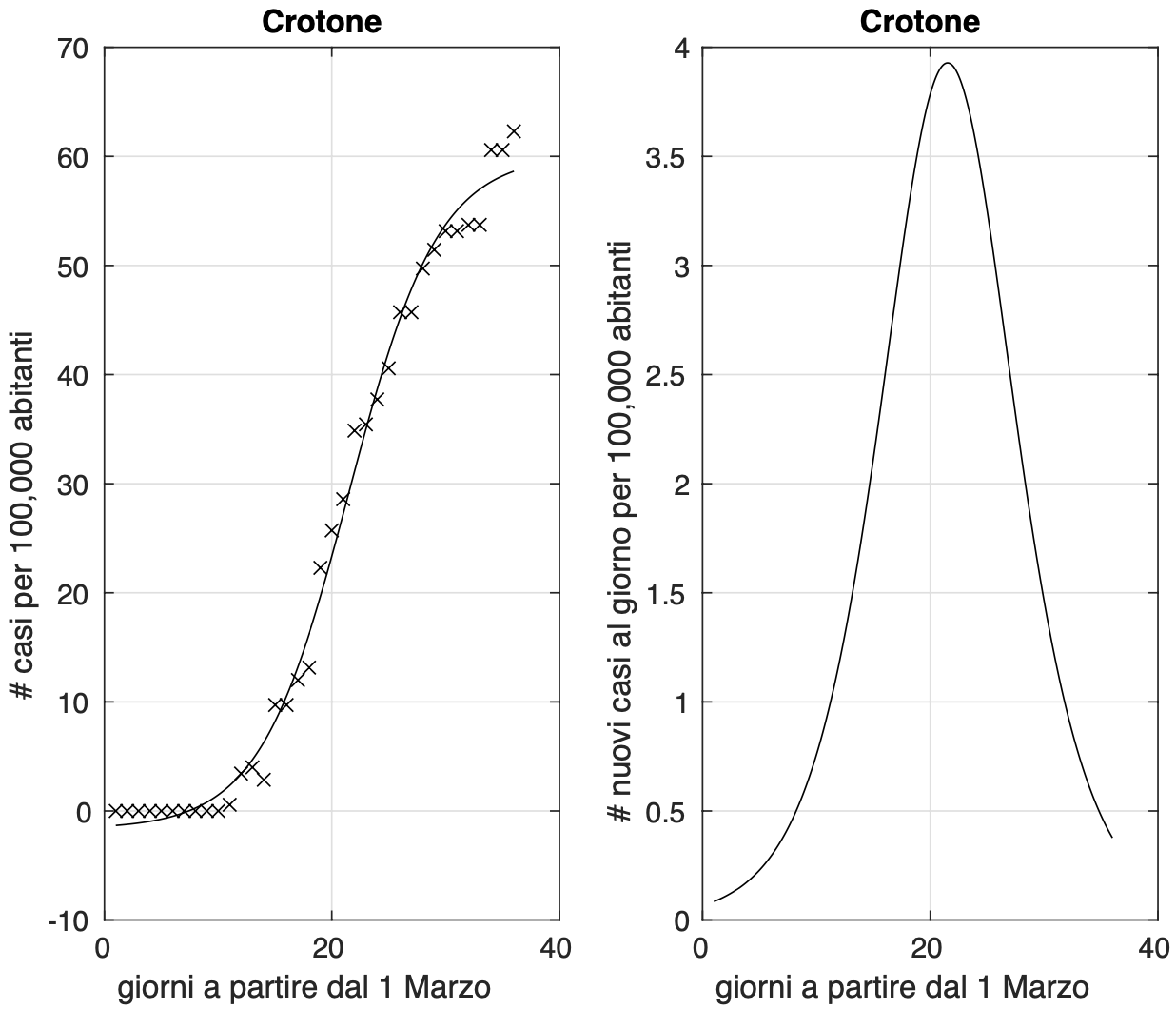
Figura 2. Sequenza del numero dei contagiati nella provincia di Crotone. Il miglior fit con un modello logistico è sovrapposto ai dati.
Note
In questo documento sono descritti i risultati relativi all’analisi per tutte le province italiane. I dati utilizzati sono quelli aggiornati alle 18 del 5 aprile 2020 e sono stati scaricati dal sito https://github.com/pcm-dpc/COVID-19/tree/master/dati-province. I risultati sostituiscono o integrano quelli nel documento del 2 aprile.
Valgono le stesse considerazioni generali del documento del 2 aprile. Alcuni chiarimenti possono essere trovati nella Nota metodologica. I risultati di tutte le province possono essere scaricati qui.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
Analisi dei dati epidemiologici del coronavirus in Italia (al 2 aprile)
- 7119 letture
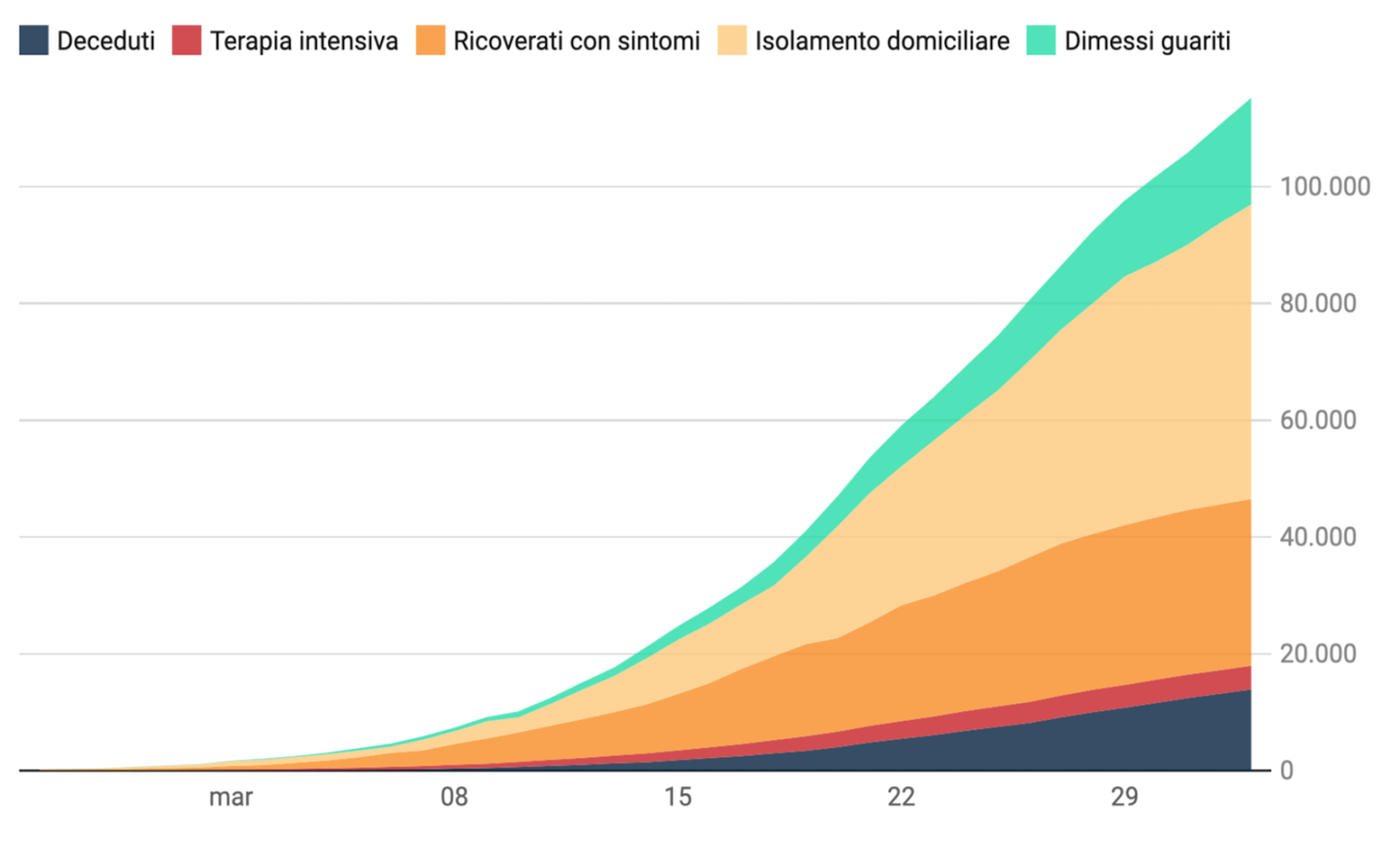
L’analisi delle sequenze temporali della frazione dei contagiati osservati rispetto alla popolazione della provincia rivela che 96 delle 107 province presentano una diminuzione del tasso di crescita. Mancano all’appello le province di Asti, Firenze, Massa e Carrara, L’Aquila, Rieti, Napoli, Campobasso, Taranto, Agrigento, Oristano e Sassari. Come si può vedere, le province ancora mancanti sono situate quasi esclusivamente al sud e nelle isole (i risultati di tutte le province analizzate possono essere scaricati qui). Questo è facilmente interpretabile alla luce del fatto che questa epidemia ha avuto un’origine localizzata in Lombardia da dove si è poi diffusa alle regioni più vicine e successivamente a quelle più lontane del sud.
Assieme a Marco Massa dell’Imperial College di Londra continuiamo a effettuare giorno per giorno un’analisi a livello regionale per la previsione del tempo in cui si stabilizzerà il numero dei contagiati osservati o equivalentemente avremo valori trascurabili del tasso di crescita di tale numero. L’analisi avviene nell’ambito statistico bayesiano ed è basata su un modello a compartimenti specifico per questo tipo di fenomeno (vedi nota metodologica). L’analisi ha rivelato che nelle tre regioni più colpite, Lombardia, Emilia Romagna e Veneto, il tasso di crescita del numero osservato dei contagiati raggiungerà valori trascurabili durante le ultime due decadi di maggio (vedi figura 1).

Figura 1. Previsione del tasso di crescita del numero di contagiati osservati in Emilia Romagna ottenuta con l’approccio statistico bayesiano basato sul modello a compartimenti.
E' molto importante sottolineare in primo luogo che questa stima può cambiare nel tempo e viene quindi aggiornata ogni giorno. Inoltre, il risultato vale se non cambierà l’ipotesi sul comportamento virtuoso degli italiani rispetto alle misure di riduzione del rischio di contagio introdotte dal governo. E quindi fondamentale che ciascuno di noi continui a fornire il proprio contributo, da solo trascurabile, ma che sommato a quelli di tutti gli altri, ha generato l’effetto osservato di frenata della diffusione dell’epidemia.
Ci occupiamo ora di alcuni aspetti che caratterizzano i pesanti effetti dell’epidemia di coronavirus sulla salute pubblica in termini di vite umane perse. Oggi ci concentriamo sull’andamento temporale dell’indice di mortalità, definito come il rapporto tra il numero di decessi e il numero di abitanti nella zona considerata. L’analisi è stata condotta a livello regionale, che è quello più fine per il quale abbiamo a disposizione i dati sui decessi. Rimandiamo al documento del 19 Marzo per alcune considerazioni sui problemi e sugli errori che influenzano il valore misurato del numero di decessi.
Abbiamo studiato quattro regioni, la Lombardia, origine della diffusione dell’epidemia in Italia e le tre regioni con essa confinanti dove si sono registrati i maggiori danni in termini sanitari: Emilia Romagna, Piemonte e Veneto.
In figura 2 mostriamo l’evoluzione nel tempo del numero di morti per coronavirus per 100,000 abitanti per le quattro regioni considerate.
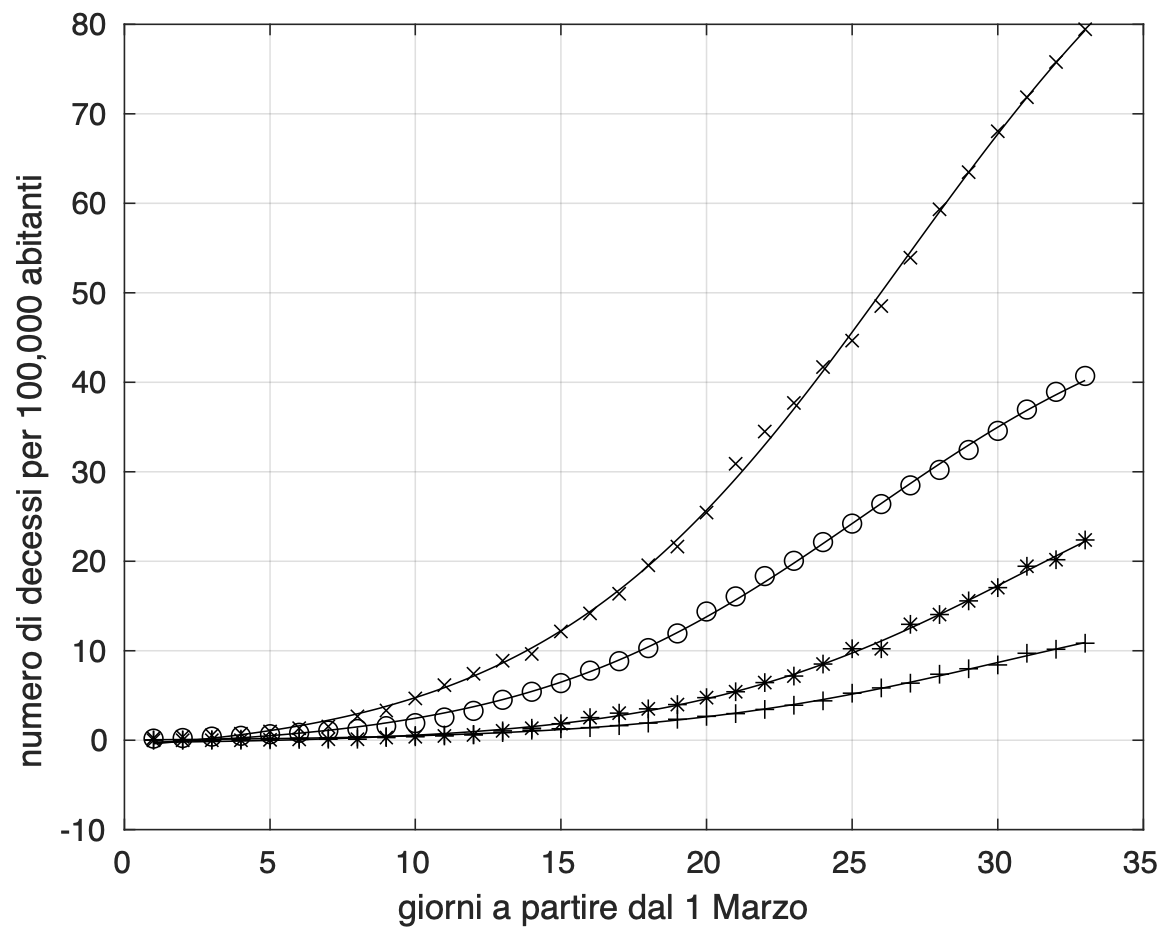
Figura 2. Andamento temporale del tasso di mortalità per coronavirus per la Lombardia (x), l’Emilia Romagna (o), il Piemonte (*) ed il Veneto (+).
I dati misurati sono stati descritti da un modello logistico (vedi nota metodologica), sovrapposto ad essi nella figura. E' da notare il comportamento virtuoso del Veneto, dove riscontriamo la curva più bassa del tasso di mortalità. Una spiegazione di ciò potrebbe essere legata al basso grado di ospedalizzazione dei pazienti nella regione Veneto, 30% circa, da confrontare per esempio con quello della Lombardia, pari circa al 60%. E' infatti noto che una via di diffusione molto efficace di questa malattia è quella nosocomiale.
A livello visivo si nota un andamento simile delle quattro curve. Questo ha suggerito di calcolare il coefficiente di determinazione per quantificare la similarità tra le curve (vedi tabella 1).
| Lombardia | Emilia Romagna | Piemonte | Veneto | |
|---|---|---|---|---|
| Lombardia | 1 | 0,9986 | 0,9795 | 0,9859 |
| Emilia Romagna | 0,9986 | 1 | 0,9728 | 0,9802 |
| Piemonte | 0.9795 | 0,9728 | 1 | 0,9973 |
| Veneto | 0,9859 | 0,9802 | 0,9973 | 1 |
Tabella 1. Valori calcolati del coefficiente di determinazione tra coppie di curve di mortalità.
Esso è il quadrato del coefficiente di correlazione lineare tra le sequenze numeriche di una generica coppia di curve ed è compreso tra zero ed uno. Tanto più il valore è vicino a uno, quanto più le curve sono simili. Dai valori della tabella possiamo dire che per due delle sei coppie di curve, Lombardia - Emilia Romagna e Piemonte - Veneto, c’è una forte similarità tra le curve della coppia. Abbiamo qundi effettuato un fit lineare per ciascuna delle due coppie (vedi figure 3 e 4). E' sorprendente la vicinanza tra i due valori stimati della costante moltiplicativa del modello lineare: 0,52 per Lombardia - Emilia Romagna e 0,49 per Piemonte - Veneto.
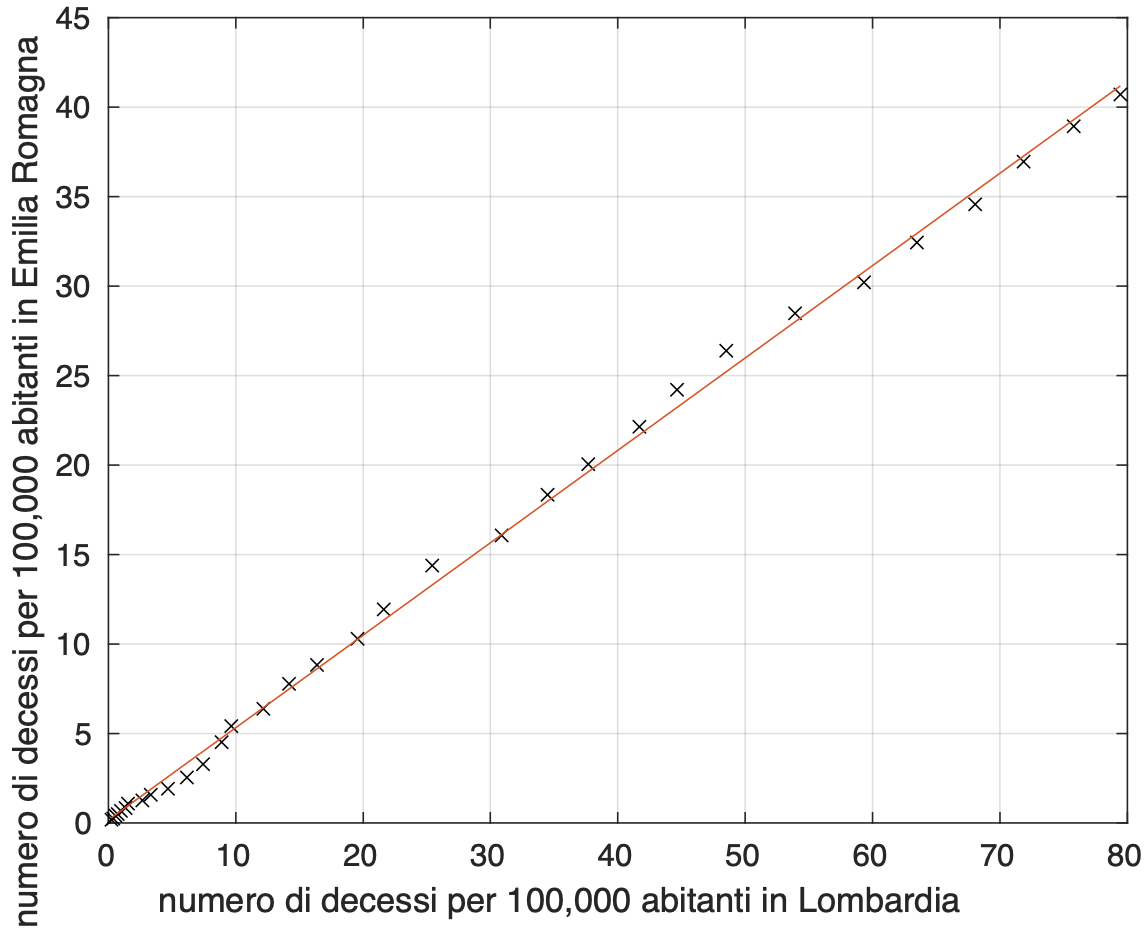
Figura 3. Dipendenza lineare tra i valori del tasso di mortalità nel tempo in Lombardia e quelli in Emilia Romagna.
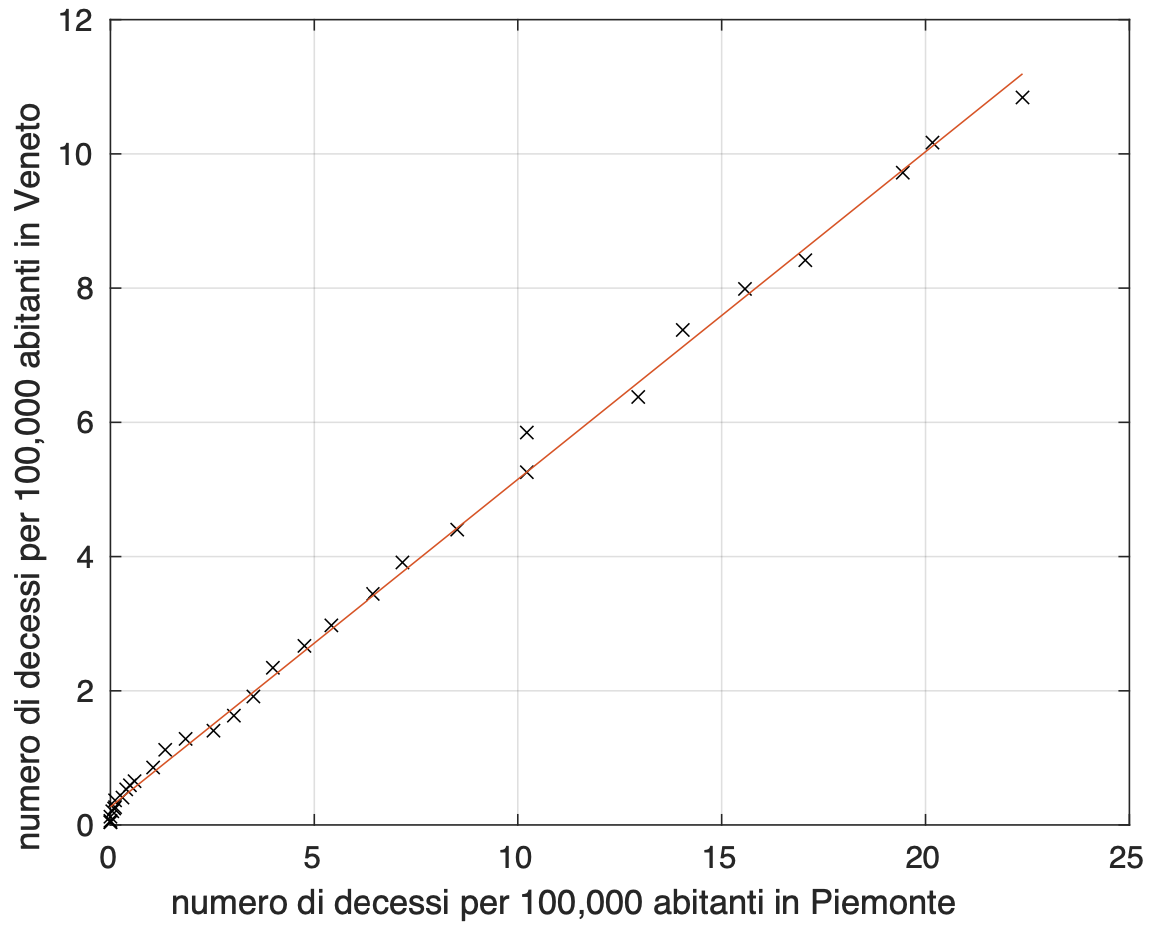
Figura 4. Dipendenza lineare tra i valori del tasso di mortalità nel tempo in Piemonte e quelli in Veneto.
Nota
In questo documento sono descritti i risultati relativi all’analisi per tutte le province di ciascuna regione. I dati utilizzati sono quelli aggiornati alle 18 del 2 Aprile 2020 e sono stati scaricati dal sito https://github.com/pcm-dpc/COVID-19/tree/master/dati-province. I risultati sostituiscono o integrano quelli nel documento del 27 Marzo. Valgono le stesse considerazioni generali del documento del 27 Marzo. Alcuni chiarimenti possono essere trovati nella Nota Metodologica. I risultati di tutte le province possono essere scaricati qui.
Scarica questo documento in versione pdf.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
Marco Massa
Dottorando e Graduate Teaching Assistant presso il Dipartimento di Matematica dell'Imperial College London
Analisi dei dati epidemiologici del coronavirus in Italia (al 27 marzo)
- 10662 letture
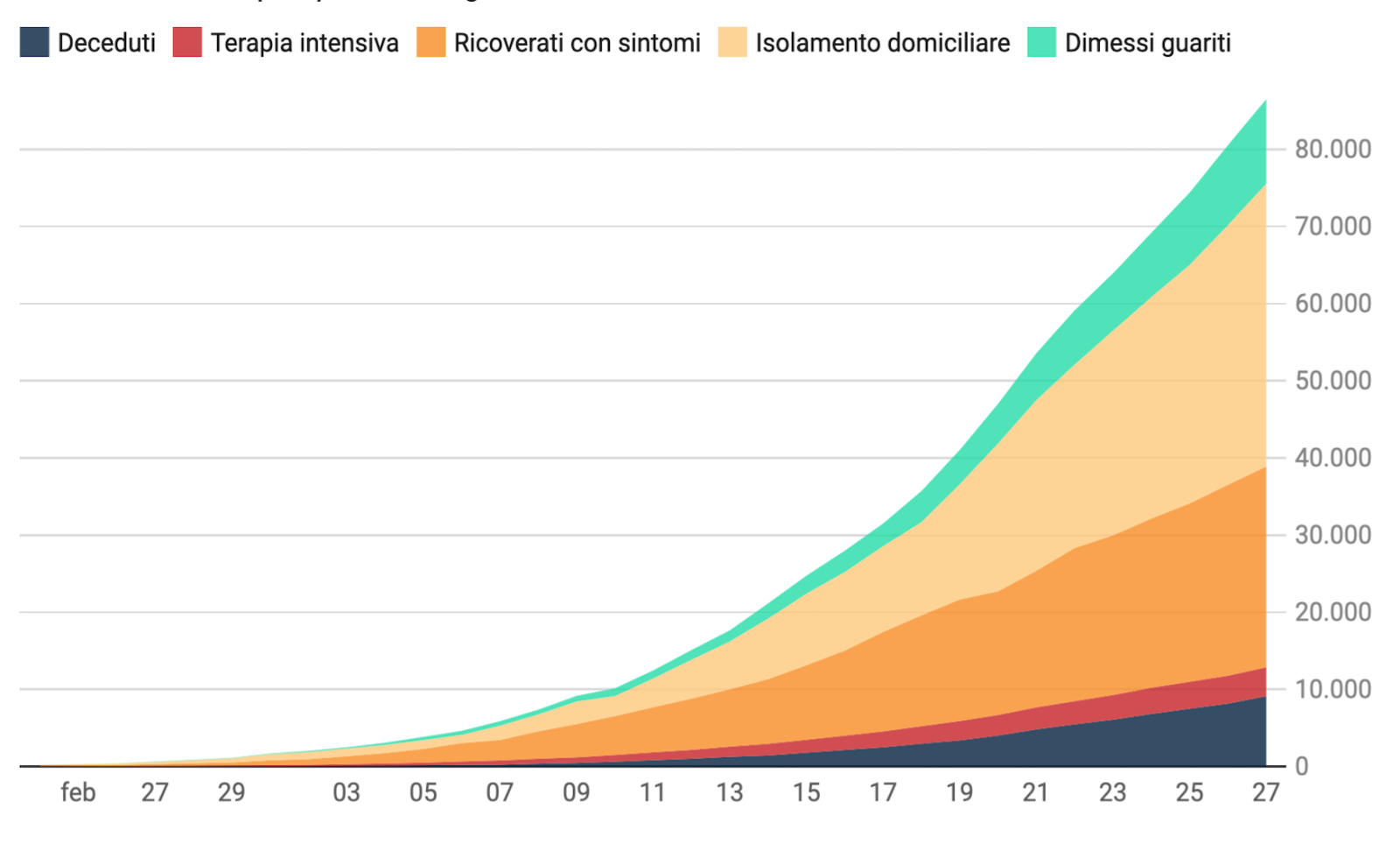
L’analisi delle sequenze temporali della frazione dei contagiati osservati rispetto alla popolazione della provincia rileva che 71 delle 107 province, presentano una diminuzione del tasso di crescita, come si osserva ad esempio per Novara nella figura 1. Abbiamo comunque considerato solo le province in cui la riduzione del tasso di crescita inizia almeno tre giorni prima del 27 marzo, ultimo giorno per cui abbiamo i dati misurati. Altre province presentavano un picco, ma era dopo il 24 marzo e sono state scartate. Domani potrebbero essere incluse anche loro. I risultati di tutte le province possono essere scaricati qui.
Le tre province di Catanzaro, La Spezia e Varese, che fino al 26 marzo avevano mostrato evidenza di aver superato il picco, hanno putroppo avuto un aumento notevole di casi diagnosticati fino al 27 marzo, come si può osservare per la provincia di Varese confrontando le figure 2 e 3. Un salto analogo è stato osservato nelle province del sud Sardegna.
Per quanto riguarda le province di Catanzaro e Sud Sardegna, l’aumento è dovuto alla positività al coronavirus di ospiti e operatori di una casa di riposo a Chiaravalle Centrale e di un’altra a Sanluri, rispettivamente. Come è stato evidenziato da Giorgio Palù, virologo dell'Università di Padova e già presidente della Società europea di virologia, la diffusione di questo virus è tipicamente nosocomiale. E' quindi molto importante, e lo sarebbe stato anche di più nelle prime fasi della diffusione di questa malattia, attuare una campagna capillare di test su tutte le strutture di sanitarie di questo tipo.
Nel caso di Varese, sembra che questo sia imputabile ad un aumento significativo del numero di tamponi effettuati, probabilmente anche ad asintomatici. Osserviamo a questo riguardo che per l’analisi dei dati sarebbe molto importante sapere se ciascun test positivo è stato effettuato su un soggetto sintomatico o meno.
Non conosciamo invece informazioni specifiche relative al caso della provincia di La Spezia.
Per la Lombardia, regione colpita per prima dal virus e dove di conseguenza è presente la maggioranza dei casi, con i dati al 26 marzo, 11 delle 12 province mostravano di aver superato il picco dei contagi. Assieme a Marco Massa, ricercatore dell’Imperial College di Londra, abbiamo quindi effettuato un’analisi a livello regionale con un modello a compartimenti specifico per questo tipo di fenomeno (vedi nota metodologica). L’analisi ha rivelato che la Lombardia si trova nella fase, seppur iniziale, di progressiva diminuzione del tasso di crescita del numero dei contagiati osservati. Tale tasso raggiungerà in pratica l’annullamento entro la metà di maggio (vedi figura 4). E molto importante sottolineare in primo luogo che questa stima è affetta da errore a causa di vari fattori, primo fra tutti il fatto che è basata sull’osservazione dei dati finora disponibili, i quali solo negli ultimi giorni contengono informazione sulla fase di diminuzione del tasso di crescita. Inoltre, il risultato vale se non cambierà l’ipotesi sul comportamento virtuoso degli italiani rispetto alle misure di riduzione del rischio di contagio introdotte dal governo. E quindi fondamentale che ciascuno di noi continui a fornire il proprio contributo, da solo trascurabile, ma che sommato a quelli di tutti gli altri, ha generato l’effetto osservato di frenata della diffusione dell’epidemia.

Figura 1. Frazione del numero di contagiati osservati nella provincia di Novara rispetto alla popolazione della provincia in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati. Si osserva una fase in cui il tasso di crescita diminuisce. La curva della frazione dei contagiati, ossia coloro che sono al momento positivi al virus, o guariti o morti è per definizione crescente, o meglio “non decrescente”. La rapidità con cui cresce la curva in un punto del tempo, il cosiddetto “tasso di crescita” si misura tramite la pendenza della retta tangente alla curva in quel punto. Più la pendenza è grande, più il tasso è grande e la curva cresce velocemente. Data una generica curva della frazione dei contagiati osservati al variare del tempo, possiamo costruire la curva che fornisce il tasso di crescita al variare del tempo. Quando il tasso inizia a diminuire la curva “flette”, cioè cambia la sua concavità da verso l’alto a verso il basso e si appiattisce. Dopo un certo tempo, la curva non mostra più in pratica nessuna variazione. Il tasso di crescita ha raggiunto la massima velocità intorno al 20 marzo, dopo questa data il tasso di crescita ha iniziato a rallentare

Figura 2. Frazione del numero di contagiati osservati nella provincia di Varese rispetto alla popolazione della provincia in funzione del tempo a partire dal 1 marzo fino al 26 marzo.
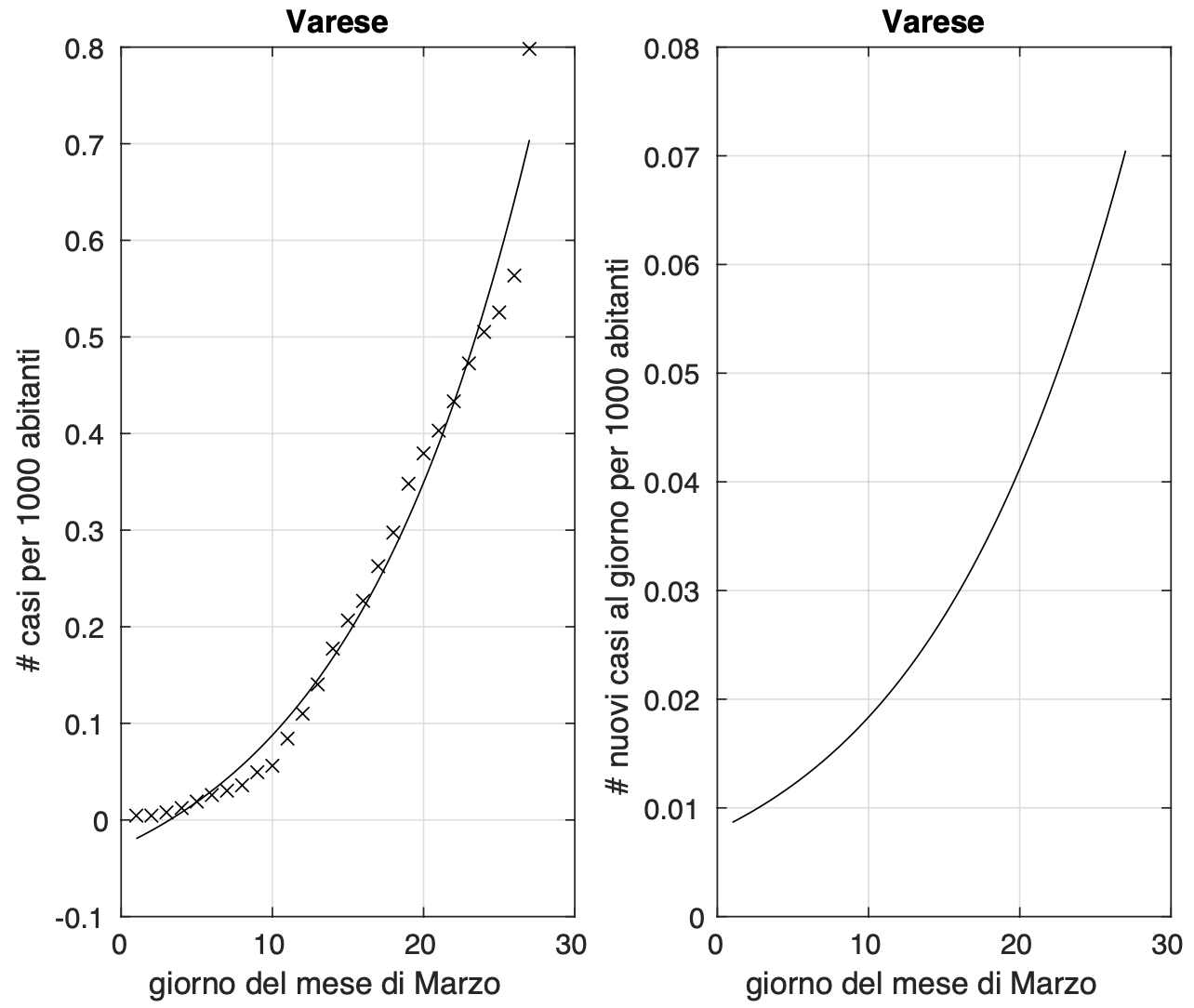
Figura 3. Frazione del numero di contagiati osservati nella provincia di Varese rispetto alla popolazione della provincia in funzione del tempo a partire dal 1 marzo fino al 27 marzo. Si nota chiaramente l’aumento notevole il 27 marzo, assolutamente anomalo rispetto all’andamento della curva nei giorni precedenti.

Figura 4. Previsione del tasso di crescita del numero di contagiati osservati in Lombardia rispetto alla popolazione della regione ottenuta col modello a compartimenti.
Note
In questo documento sono descritti i risultati relativi all’analisi per tutte le province di ciascuna regione. I risultati sostituiscono o integrano quelli nel documento del 25 marzo. I dati utilizzati sono quelli aggiornati alle 18 del 27 marzo 2020 e sono stati scaricati dal sito https://github.com/pcm-dpc/COVID-19/tree/master/dati-province.
Valgono le stesse considerazioni generali del documento del 25 marzo. Alcuni chiarimenti possono essere trovati nella Nota metodologica.
Scarica questo documento in versione pdf.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
Marco Massa
Dottorando e Graduate Teaching Assistant presso il Dipartimento di Matematica dell'Imperial College London
Analisi dei dati epidemiologici del coronavirus in Italia (al 25 marzo)
- 9579 letture
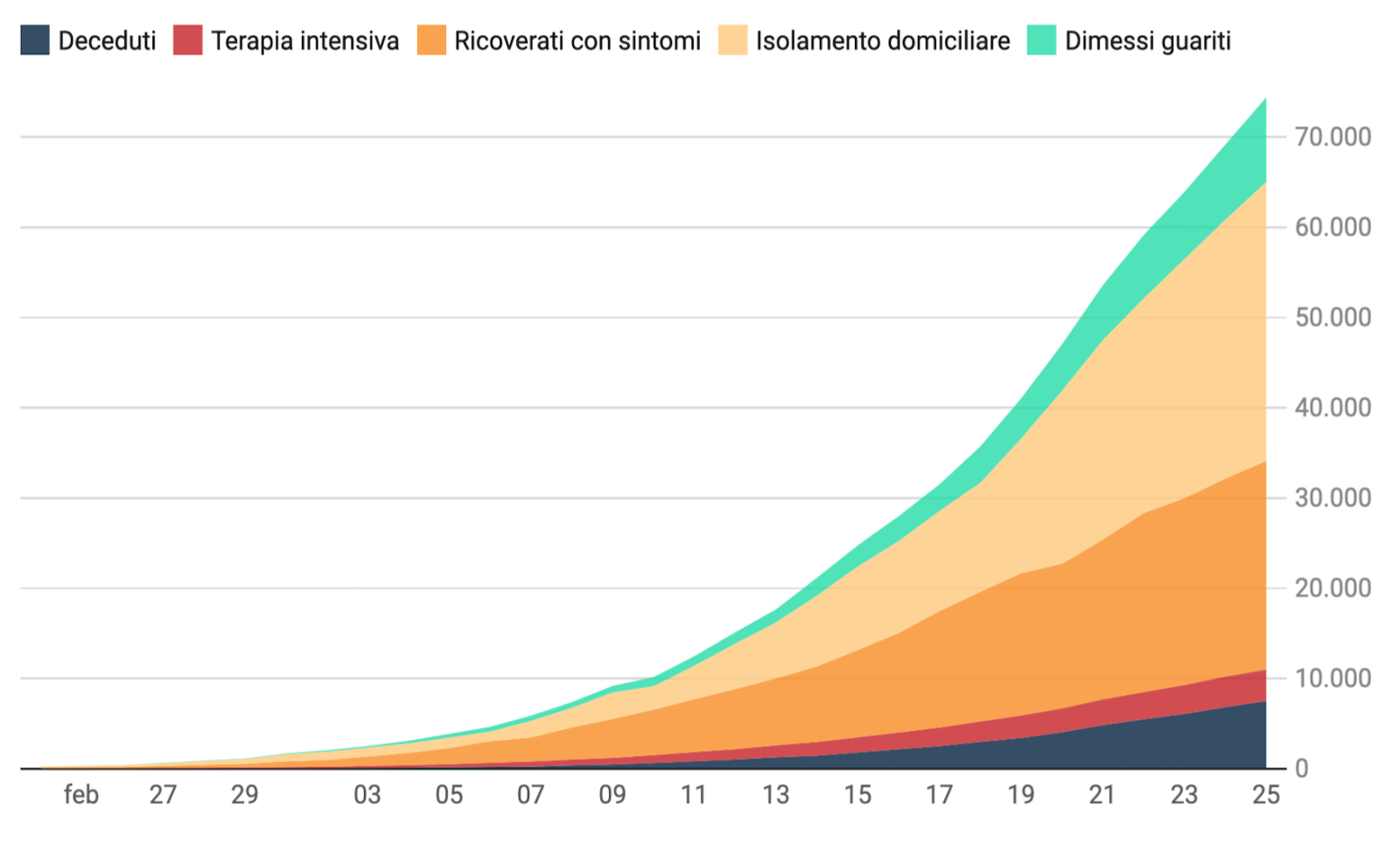
L’analisi delle sequenze temporali della frazione dei contagiati osservati rispetto alla popolazione della provincia rileva che 69 province, poco meno di 2/3 delle 107 province presentano una diminuzione del tasso di crescita, come si osserva a esempio per Novara nelle figure 1 e 2.
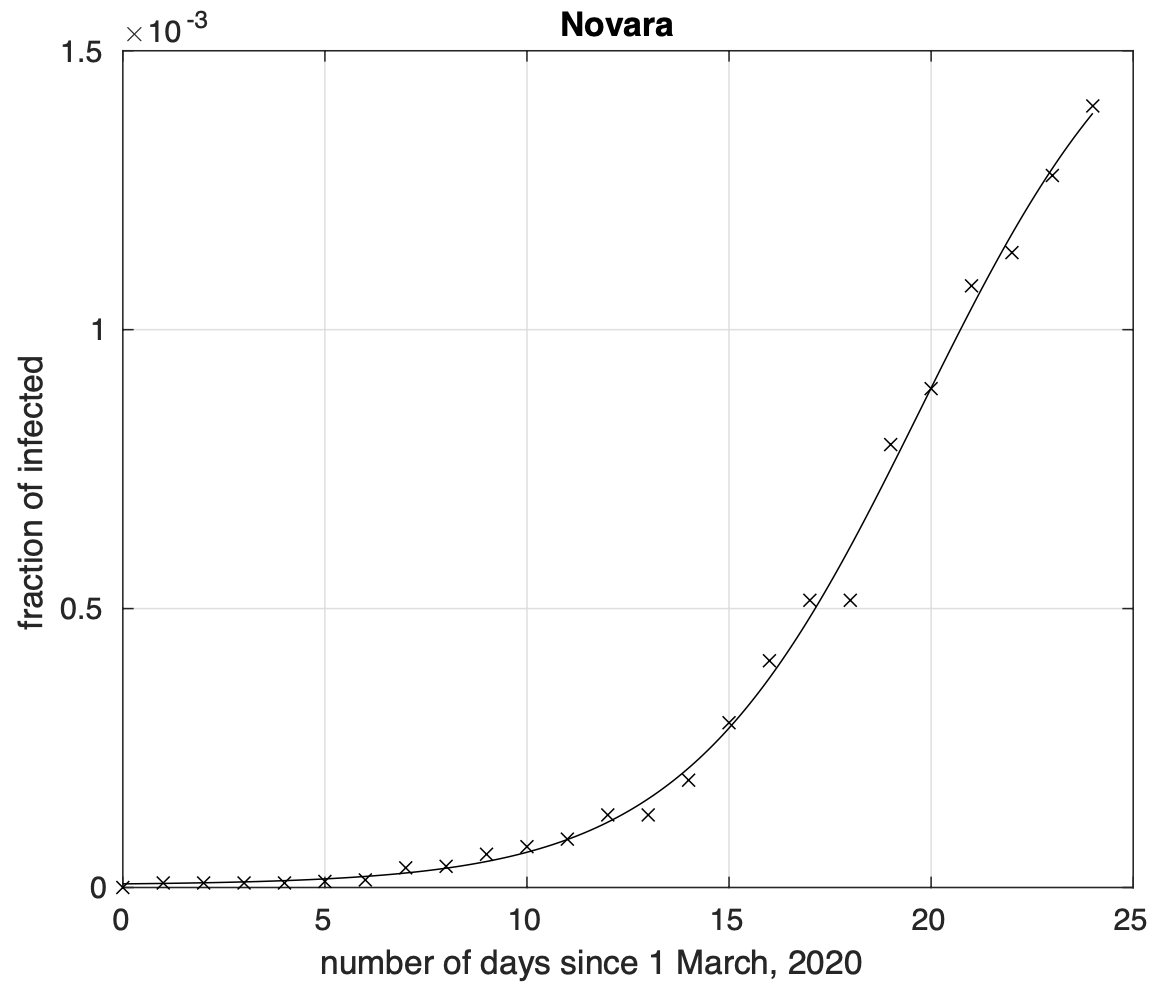
Figura 1. Frazione del numero di contagiati osservati nella provincia di Novara rispetto alla popolazione della provincia in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati (le crocette). Si osserva una fase in cui il tasso di crescita diminuisce. La curva della frazione dei contagiati, ossia coloro che sono al momento positivi al virus, o guariti o morti è per definizione crescente, o meglio “non decrescente”. La rapidità con cui cresce la curva in un punto del tempo, il cosiddetto “tasso di crescita” si misura tramite la pendenza della retta tangente alla curva in quel punto. Più la pendenza è grande, più il tasso è grande e la curva cresce velocemente. Data una generica curva della frazione dei contagiati osservati al variare del tempo, possiamo costruire la curva che fornisce il tasso di crescita al variare del tempo. Quando il tasso inizia a diminuire la curva “flette”, cioè cambia la sua concavità da verso l’alto a verso il basso e si appiattisce. Dopo un certo tempo, la curva non mostra più in pratica nessuna variazione.
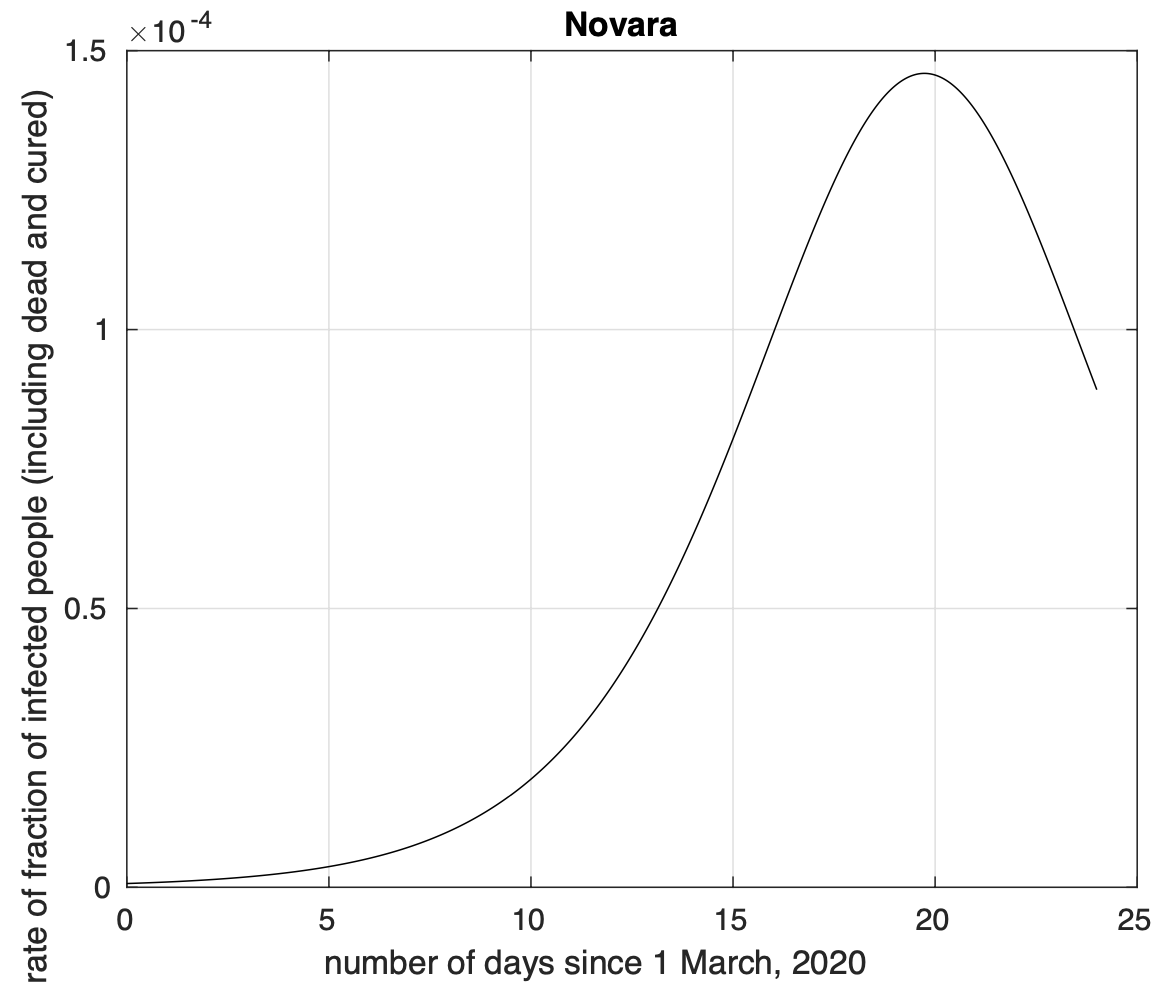
Figura 2. Tasso di crescita della frazione del numero di contagiati osservati a Novara rispetto alla popolazione della provincia in funzione del tempo a partire dal 1 marzo. Il tasso di crescita ha raggiunto la massima velocità il 20 marzo, dopo questa data il tasso di crescita ha iniziato a rallentare. Il modello teorico adottato è quello logistico che appare in figura 1.
Abbiamo comunque considerato solo le province in cui la riduzione del tasso di crescita inizia almeno tre giorni prima del 25 marzo, ultimo giorno per cui abbiamo i dati misurati. Altre province presentavano un picco, ma era dopo il 22 marzo e sono state scartate. Domani potrebbero essere incluse anche loro (le curve per tutte le province analizzate al 25 marzo sono scaricabili qui).
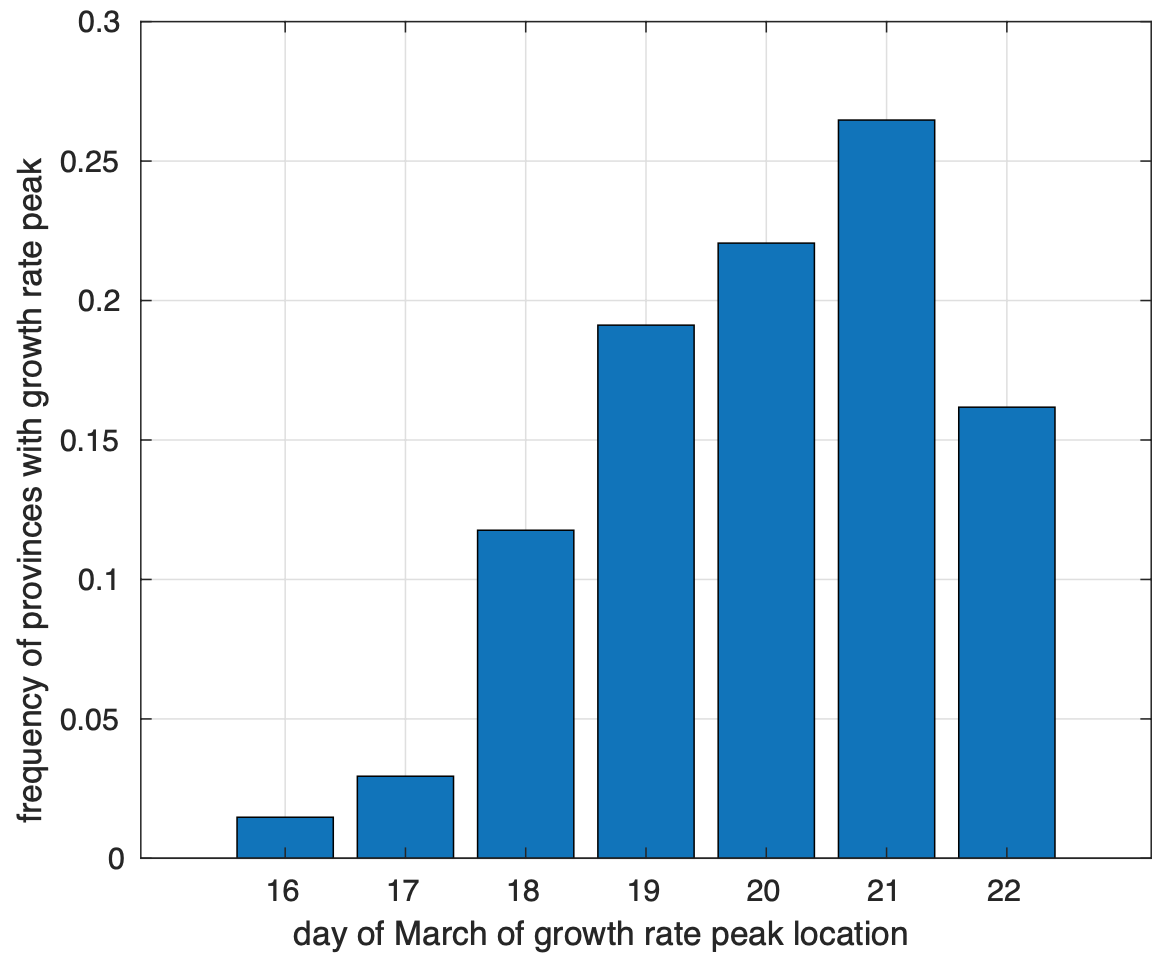
Figura 3. Istogramma per le province del giorno di marzo in cui si osserva il picco del tasso di crescita della frazione del numero di contagiati osservati.
Nella figura 3 osserviamo l’istogramma dei valori osservati per le province del giorno di marzo dove la curva del tasso di crescita inverte la tendenza ed inizia a diminuire. Abbiamo escluso la provincia di Lodi che mostra una riduzione del tasso già dal 1 marzo. Si nota che l’istogramma è asimmetrico. Questo è dovuto al troncamento dei dati indotto dalla regola scelta seguendo la quale abbiamo scartato i casi dove il massimo della curva del tasso di crescita non avveniva almeno tre giorni prima del 25 marzo. Ci aspettiamo che nei prossimi giorni l’istogramma diventi sempre più simmetrico. Il giorno in cui si trova in media il picco è il 20 marzo. Questo corrisponde ad una distanza di 9 giorni dall’11 marzo quando sono state introdotte le misure di limitazione della mobilità. Ricordiamo che per questa infezione, tra il contagio e l’insorgenza dei sintomi ci sono in media 5 giorni circa, mentre bisogna aspettare ancora 4 giorni per arrivare alla diagnosi. Questo risultato fornisce evidenza a supporto dell’ipotesi che la diminuzione del tasso sia stata causata dalla riduzione della diffusione indotta dalle misure di limitazione della mobilità introdotte l’11 marzo col decreto “Io resto a casa”. Nei prossimi giorni vedremo se questo risultato verrà confermato.
Undici delle 12 province della regione più colpita, la Lombardia, presentano la riduzione del tasso, manca all’appello la provincia di Como. Tutte le regioni sono interessate con le province così distribuite: 2 in Abruzzo, 1 in Basilicata, 3 in Calabria, 2 in Campania, 5 in Emilia, 2 in Friuli, 1 nel Lazio, tutte le 4 della Liguria, 11 in Lombardia, 4 nelle Marche, 1 nel Molise, 6 in Piemonte, 4 in Puglia, 1 in Sardegna, 6 in Sicilia, 8 in Toscana, 1 in Trentino, 2 in Umbria, 1 in Valle D’Aosta e 4 nel Veneto. Questa distribuzione spaziale ci indica che la riduzione del tasso di crescita sia probabilmente influenzato da un unico fattore indipendentemente dalla provincia. Ipotizziamo che tale fattore sia costituito dalle misure di restrizione della mobilità introdotte a livello nazionale l’11 marzo col decreto “Io resto a casa”.
Nota
In questo documento sono descritti i risultati relativi all’analisi per tutte le province di ciascuna regione. I risultati sostituiscono o integrano quelli nel documento del 23 marzo. I dati utilizzati sono quelli aggiornati alle 18 del 25 marzo 2020 e sono stati scaricati dal sito https://github.com/pcm-dpc/COVID-19/tree/master/dati-province. Valgono le stesse considerazioni generali del documento del 23 marzo. Alcuni chiarimenti possono essere trovati nella Nota metodologica. (Scarica il documento in versione pdf).
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
Analisi dei dati epidemiologici del coronavirus in Italia (al 23 marzo)
- 11558 letture
L’analisi delle sequenze temporali della frazione dei contagiati osservati rispetto alla popolazione della provincia rileva che 57 delle 107 province presentano una diminuzione del tasso di crescita, come si osserva ad esempio per Brindisi nelle figure 1 e 2 (le curve per tutte le province sono scaricabili qui). Abbiamo comunque considerato solo le province in cui la riduzione del tasso di crescita inizia almeno tre giorni prima del 23 marzo, ultimo giorno per cui abbiamo i dati misurati. Osserviamo che ieri le analoghe province che mostravano una diminuzione del tasso di crescita erano 31.
Nella figura 3 osserviamo l’istogramma dei valori osservati per le province del giorno di marzo dove la curva del tasso di crescita inverte la tendenza e inizia a diminuire. Abbiamo escluso la provincia di Lodi che mostra una riduzione del tasso già dal 1 marzo. Come si osserva, il valore più frequente corrisponde al 20 marzo. Si nota che l’istogramma è asimmetrico. Questo è dovuto al troncamento dei dati indotto dalla regola scelta seguendo la quale abbiamo scartato i casi dove il massimo della curva del tasso di crescita non avveniva almeno tre giorni prima del 23 marzo. Ci aspettiamo che nei prossimi giorni l’istogramma diventi sempre più simmetrico. Se questo accadrà, avremo che la media di tale giorno corrisponderà al 20 marzo. Osserviamo che comunque, al momento questo è il valore più probabile. Questo corrisponde a una distanza di 9 giorni dall’11 marzo quando sono state introdotte le misure di limitazione della mobilità. Ricordiamo che per questa infezione, tra il contagio e l’insorgenza dei sintomi ci sono in media 5 giorni circa, mentre bisogna aspettare ancora 4 giorni per arrivare alla diagnosi. Questo risultato fornisce evidenza a supporto dell’ipotesi che la diminuzione del tasso sia stata causata dalla riduzione della diffusione indotta dalle misure di limitazione della mobilità introdotte l’11 marzo col decreto “Io resto a casa”. Nei prossimi giorni vedremo se questo risultato verrà confermato.
Dieci delle 12 province della regione più colpita, la Lombardia, presentano la riduzione del tasso e finalmente anche Milano mostra la riduzione del tasso di crescita (vedi figure 4 e 5). Tutte le regioni sono interessate con le province così distribuite: 2 in Abruzzo, 1 in Basilicata, 3 in Calabria, 2 in Campania, 2 in Emilia, 1 in Friuli, 4 nel Lazio dove manca Roma, 3 in Liguria, 10 in Lombardia, 2 nelle Marche, 1 nel Molise, 3 in Piemonte, 3 in Puglia, 4 in Sardegna, 5 in Sicilia, 5 in Toscana, 1 in Trentino, 2 in Umbria, 1 in Valle D’Aosta e 2 nel Veneto. Questa distribuzione spaziale ci indica che la riduzione del tasso di crescita sia probabilmente influenzato da un unico fattore indipendentemente dalla provincia. Ipotizziamo che tale fattore sia costituito dalle misure di restrizione della mobilità introdotte a livello nazionale l’11 marzo col decreto “Io resto a casa”.
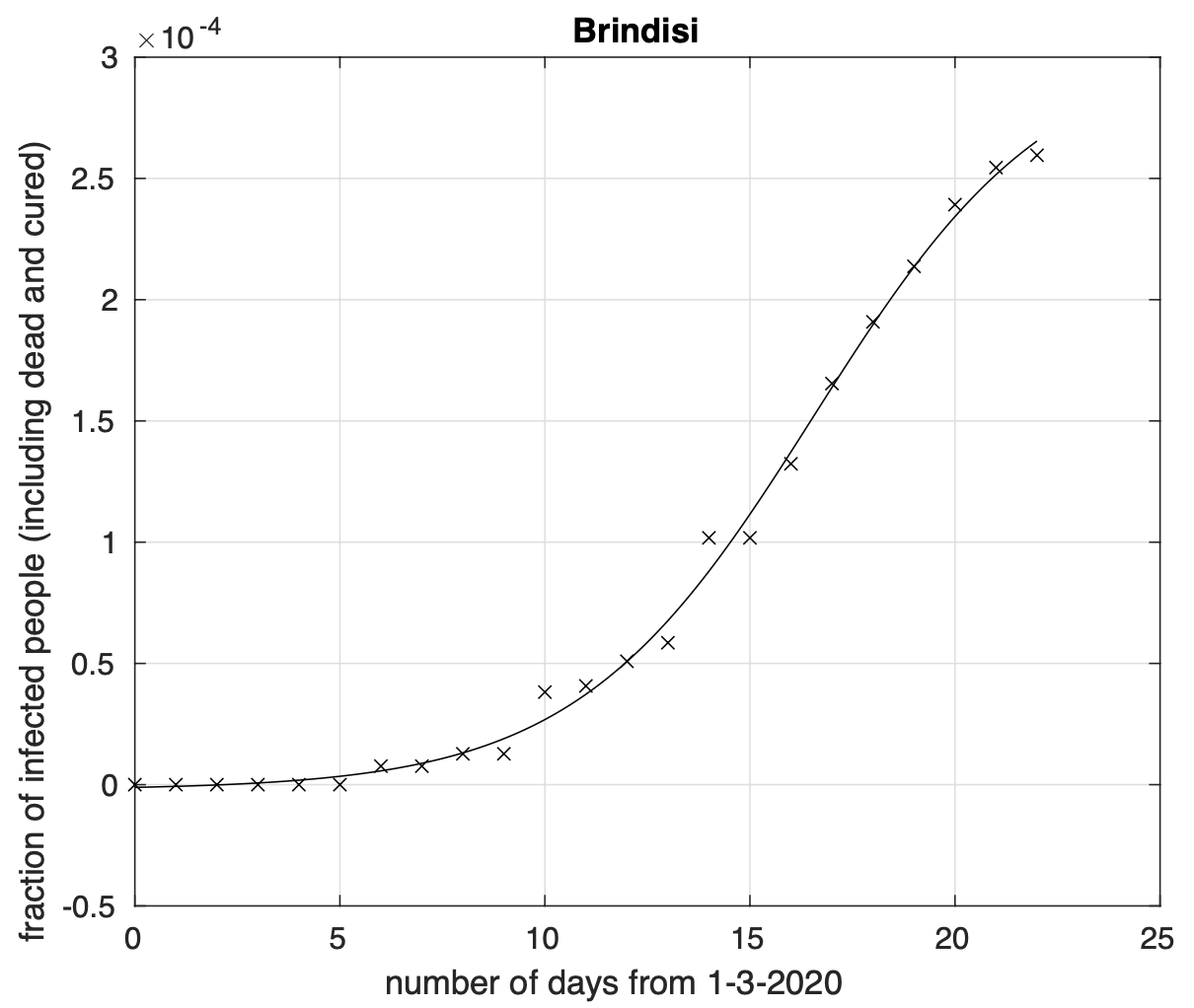
Figura 1. Frazione del numero di contagiati osservati nella provincia di Brindisi rispetto alla popolazione della provincia in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati. Si osserva una fase in cui il tasso di crescita diminuisce. La curva della frazione dei contagiati, ossia coloro che sono al momento positivi al virus, o guariti o morti è per definizione crescente, o meglio “non decrescente”. La rapidità con cui cresce la curva in un punto del tempo, il cosiddetto “tasso di crescita” si misura tramite la pendenza della retta tangente alla curva in quel punto. Più la pendenza è grande, più il tasso è grande e la curva cresce velocemente. Data una generica curva della frazione dei contagiati osservati al variare del tempo, possiamo costruire la curva che fornisce il tasso di crescita al variare del tempo. Quando il tasso inizia a diminuire la curva “flette”, cioè cambia la sua concavità da verso l’alto a verso il basso e si appiattisce. Dopo un certo tempo, la curva non mostra più in pratica nessuna variazione.
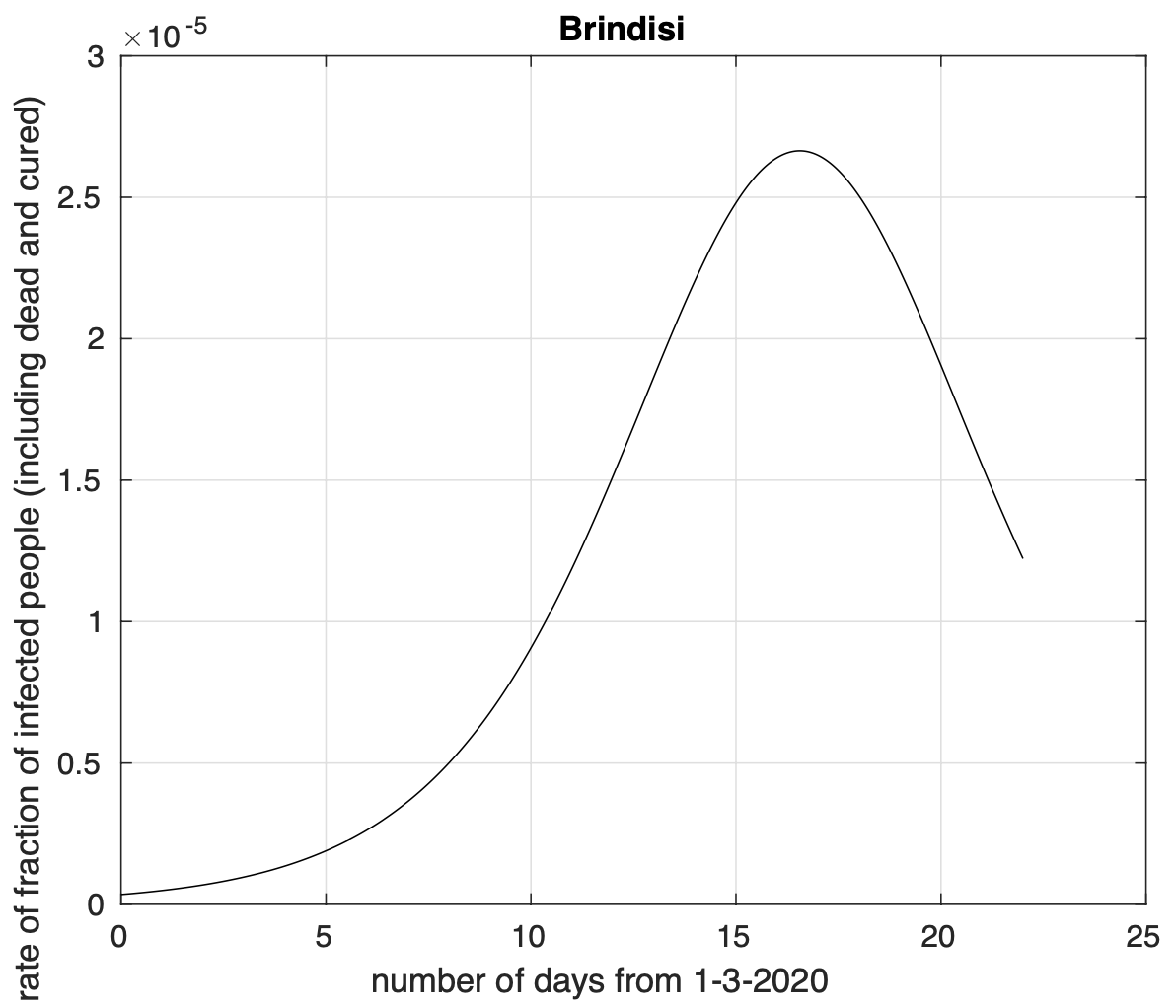
Figura 2. Tasso di crescita della frazione del numero di contagiati osservati a Brindisi rispetto alla popolazione della provincia in funzione del tempo a partire dal 1 marzo. Il modello teorico adottato è quello logistico che appare in figura 1.
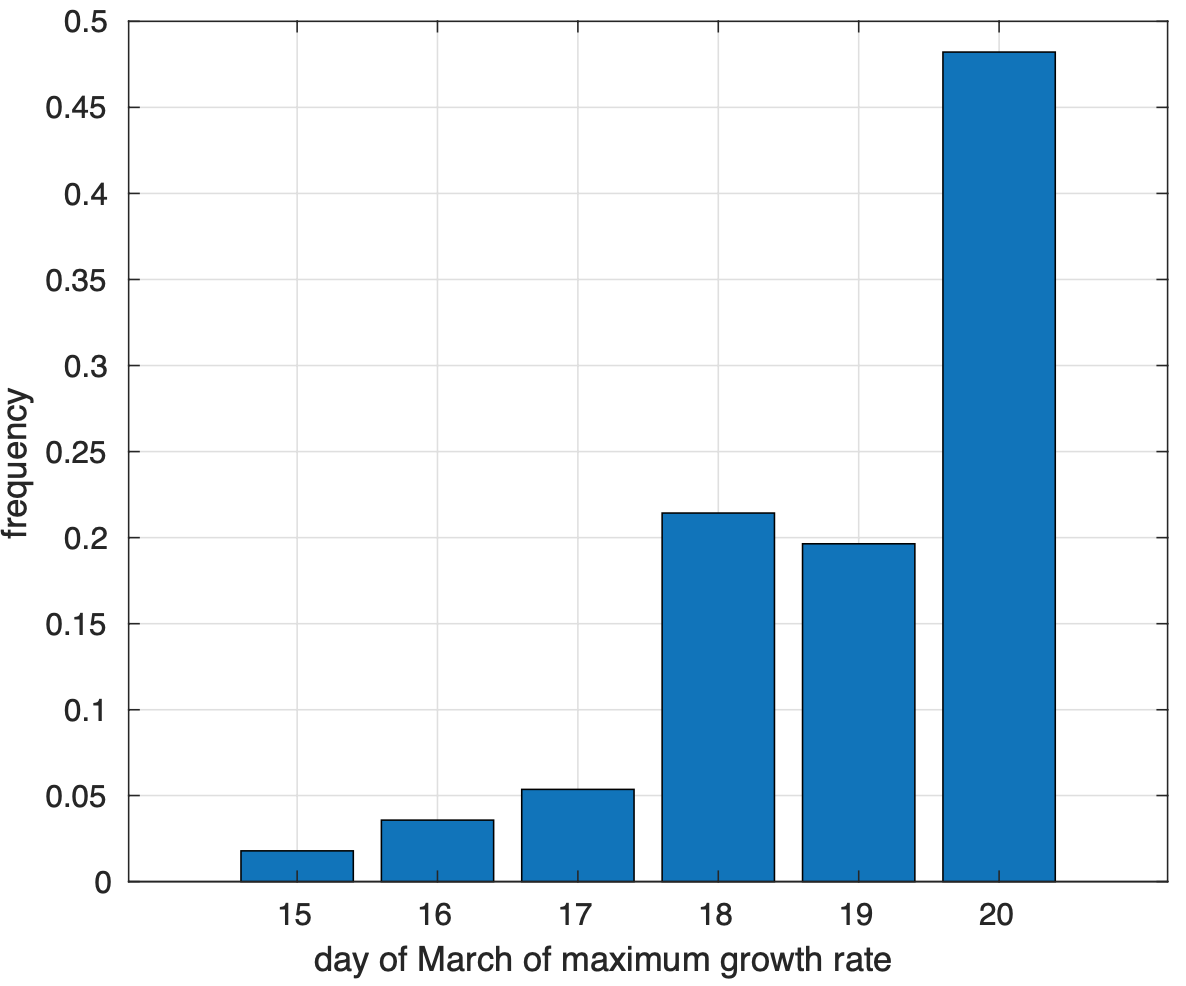
Figura 3. Istogramma per le province del giorno di marzo in cui si osserva il picco del tasso di crescita della frazione del numero di contagiati osservati.

Figura 4. Frazione del numero di contagiati osservati nella provincia di Milano rispetto alla popolazione della provincia in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati. Si osserva una fase in cui il tasso di crescita diminuisce.

Figura 5. Tasso di crescita della frazione del numero di contagiati osservati a Milano rispetto alla popolazione della provincia in funzione del tempo a partire dal 1 marzo. Il modello teorico adottato è quello logistico della figura 4.
Note
In questo documento sono descritti i risultati relativi all’analisi per tutte le province di ciascuna regione. I risultati sostituiscono o integrano quelli nel documento del 22 marzo. I dati utilizzati sono quelli aggiornati alle 18 del 23 marzo 2020 e sono stati scaricati dal sito https://github.com/pcm-dpc/COVID-19/tree/master/dati-province. Valgono le stesse considerazioni generali del documento del 22 marzo. Alcuni chiarimenti possono essere trovati nella nota metodologica. (Scarica il documento in versione pdf).
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
Analisi dei dati epidemiologici del coronavirus in Italia (al 22 marzo)
- 7717 letture
In questo documento sono descritti i risultati relativi all’analisi per tutte le province di ciascuna regione. I risultati sostituiscono o integrano quelli nel documento del 21 marzo. I dati utilizzati sono quelli aggiornati alle 18 del 22 marzo 2020 e sono stati scaricati dal sito https://github.com/pcm-dpc/COVID-19/tree/master/dati-province.
Valgono le stesse considerazioni generali del documento del 21 marzo. Alcuni chiari- menti possono essere trovati nella Nota Metodologica. L’analisi delle sequenze temporali della frazione dei contagiati osservati rispetto alla popolazione della provincia rileva che la maggioranza delle 107 province presenta una diminuzione del tasso di crescita, come si osserva ad esempio per Brindisi nelle figure 1 e 2. Le curve per tutte le province sono scaricabili qui. Ipotizziamo che la diminuzione del tasso sia stata causata dalla riduzione della diffusione indotta dalle misure di limitazione della mobilità introdotte l’11 marzo col decreto “Io resto a casa”, come motivato nel seguito.
Abbiamo comunque considerato solo le 31 province in cui la riduzione del tasso di crescita inizia almeno tre giorni prima del 22 marzo, ultimo giorno per cui abbiamo i dati misurati. Sette delle 12 province della regione più colpita, la Lombardia, presentano la riduzione del tasso, come si può osservare nella tabella 1 relativa alle regioni del nord, mentre i risultati per le regioni del centro e del sud sono contenuti nelle tabelle 2 e 3 rispettivamente. Notiamo che la distribuzione per area geografica non si mostra molto disomogenea. Infatti, abbiamo tre regioni situate nel nord e quattro sia nel centro che nel sud. Stessa conclusione a livello di province, con 12 province al nord, 8 al centro ed 11 al sud. Anche a livello del giorno di marzo in cui avviene l’inversione di tendenza, non ci sono grandi differenze tra gruppi, sia a livello di regione che di zona geografica (nord, centro, sud e isole), col range stimato per tale giorno pari a 15-19 marzo. Questo ci dice che il fenomeno è molto probabilmente influenzato da un unico fattore indipendentemente dalla provincia. Ipotizziamo che tale fattore sia costituito dalle misure di restrizione della mobilità introdotte a livello nazionale l’11 marzo col decreto “Io resto a casa”. Le stime ottenute per il giorno dell’inversione sono compatibili con la data dell’11 marzo e con i tempi tipici dello sviluppo della malattia. Infatti, tra il contagio e l’insorgenza dei sintomi ci sono in media 5 giorni circa, con un range tra 2 e 12 giorni, fino ad un massimo di 14 giorni, mentre bisogna aspettare ancora 4 giorni per arrivare alla diagnosi. Considerando il massimo del tempo tra infezione e diagnosi, arriviamo a 16-18 giorni. I prossimi 7 giorni saranno quindi critici. Se vedremo un progressivo incremento del numero di province che presentano evidenza di riduzione del tasso di crescita fino a raggiungere un massimo tra sette giorni, potremmo essere confidenti della veridicità di questa ipotesi.
| Lombardia | Bergamo 18 |
Brescia 17 |
Cremona 16 |
Lodi 1 |
Pavia 17 |
Sondrio 19 |
Varese 17 |
|---|---|---|---|---|---|---|---|
| Liguria | Genova 18 |
La Spezia 15 |
Savona 17 |
||||
| Emilia | Forlì-Cesena 19 |
Piacenza 17 |
Tabella 1. Valori stimati del giorno di marzo in cui appare l’inversione della tendenza (da aumento a diminuzione) del tasso di crescita (in giorni) della frazione di contagiati osservati nelle regioni del nord Italia.
| Toscana | Arezzo 17 |
Grosseto 18 |
Massa Carrara 19 |
|---|---|---|---|
| Lazio | Frosinone 16 |
Rieti 18 |
|
| Abruzzo | Pescara 18 |
Teramo 19 |
|
| Marche | Pesaro-Urbino 17 |
Tabella 2. Valori stimati del giorno di marzo in cui appare l’inversione della tendenza (da aumento a diminuzione) del tasso di crescita (in giorni) della frazione di contagiati osservati nelle regioni del centro Italia.
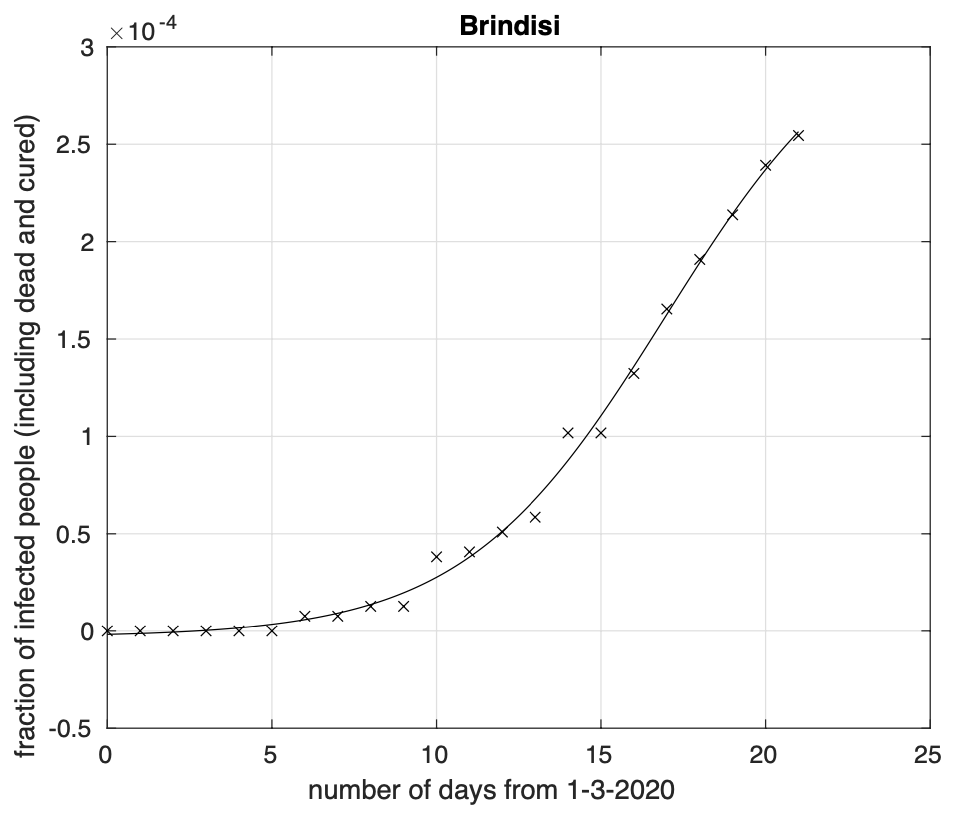
Figura 1. Frazione del numero di contagiati osservati nella provincia di Brindisi rispetto alla popolazione della provincia in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati. Si osserva una fase in cui il tasso di crescita diminuisce. La curva della frazione dei contagiati, ossia coloro che sono al momento positivi al virus, o guariti o morti è per definizione crescente, o meglio “non decrescente”. La rapidità con cui cresce la curva in un punto del tempo, il cosiddetto “tasso di crescita” si misura tramite la pendenza della retta tangente alla curva in quel punto. Più la pendenza è grande, più il tasso è grande e la curva cresce velocemente. Data una generica curva della frazione dei contagiati osservati al variare del tempo, possiamo costruire la curva che fornisce il tasso di crescita al variare del tempo. Quando il tasso inizia a diminuire la curva “flette”, cioè cambia la sua concavità da verso l’alto a verso il basso e si appiattisce. Dopo un certo tempo, la curva non mostra più in pratica nessuna variazione.

Figura 2. Tasso di crescita della frazione del numero di contagiati osservati a Brindisi rispetto alla popolazione della provincia in funzione del tempo a partire dal 1 marzo. Il modello teorico adottato è quello logistico.
| Calabria | Catanzaro 18 |
Reggio Calabria 18 |
|||
|---|---|---|---|---|---|
| Puglia | Brindisi 18 |
||||
| Sicilia | Caltanisetta 19 |
Enna 19 |
Ragusa 18 |
Siracusa 18 |
Trapani 18 |
| Sardegna | Cagliari 18 |
Nuoro 17 |
Sud Sardegna 15 |
Tabella 3. Valori stimati giorno di marzo un cui appare l’inversione della tendenza (da aumento a diminuzione) del tasso di crescita (in giorni) della frazione di contagiati osservati nelle regioni del sud Italia ed isole.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
Analisi dei dati epidemiologici del coronavirus in Italia (al 21 marzo)
- 12439 letture
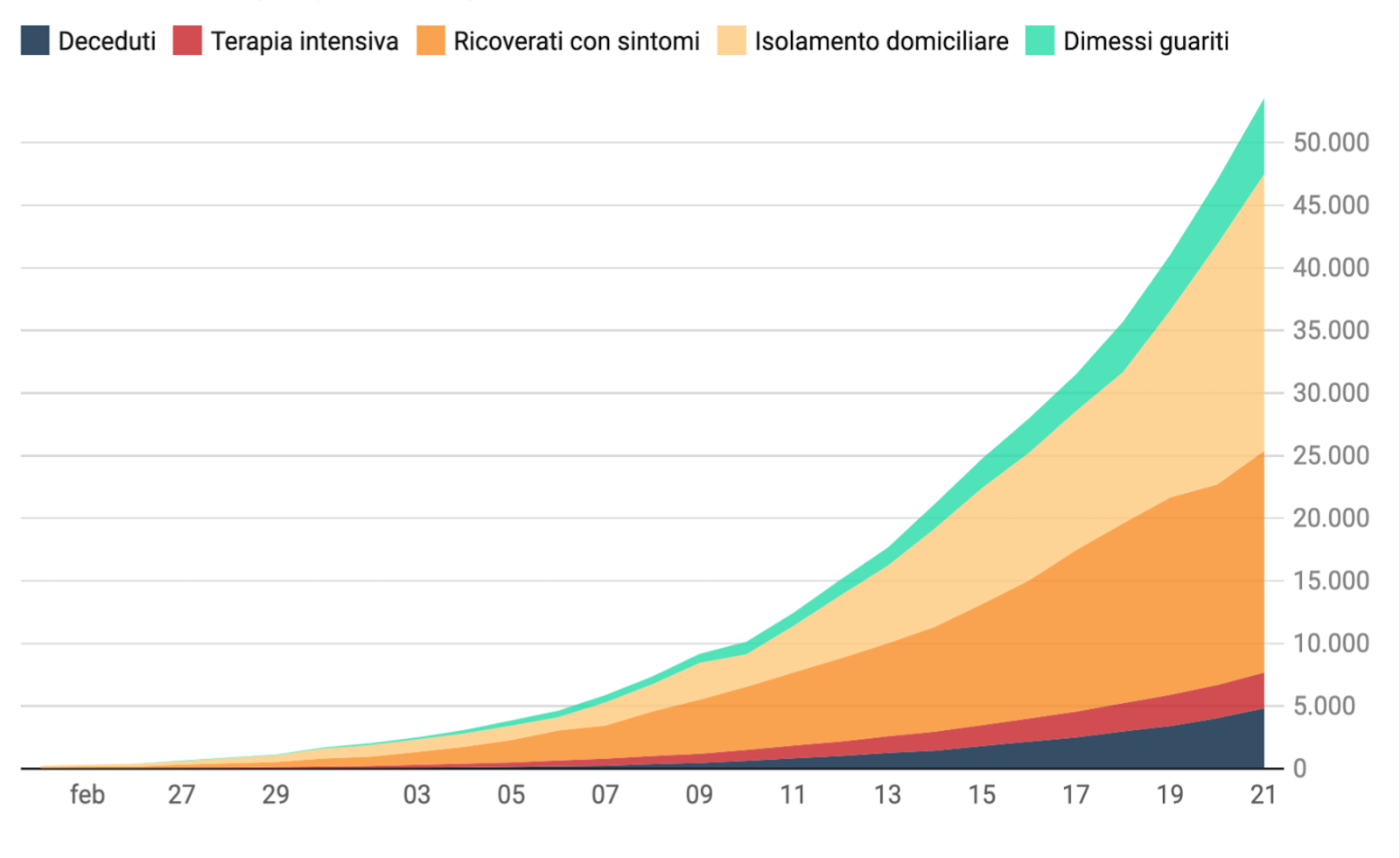
In questo documento sono descritti i risultati relativi all’analisi per tutte le province di ciascuna regione. I risultati sostituiscono o integrano quelli nel documento del 20 Marzo. I dati utilizzati sono quelli aggiornati alle 18 del 21 Marzo 2020 e sono stati scaricati dal sito https://github.com/pcm-dpc/COVID-19/tree/master/dati-province. Valgono le stesse considerazioni generali del documento del 20 marzo.
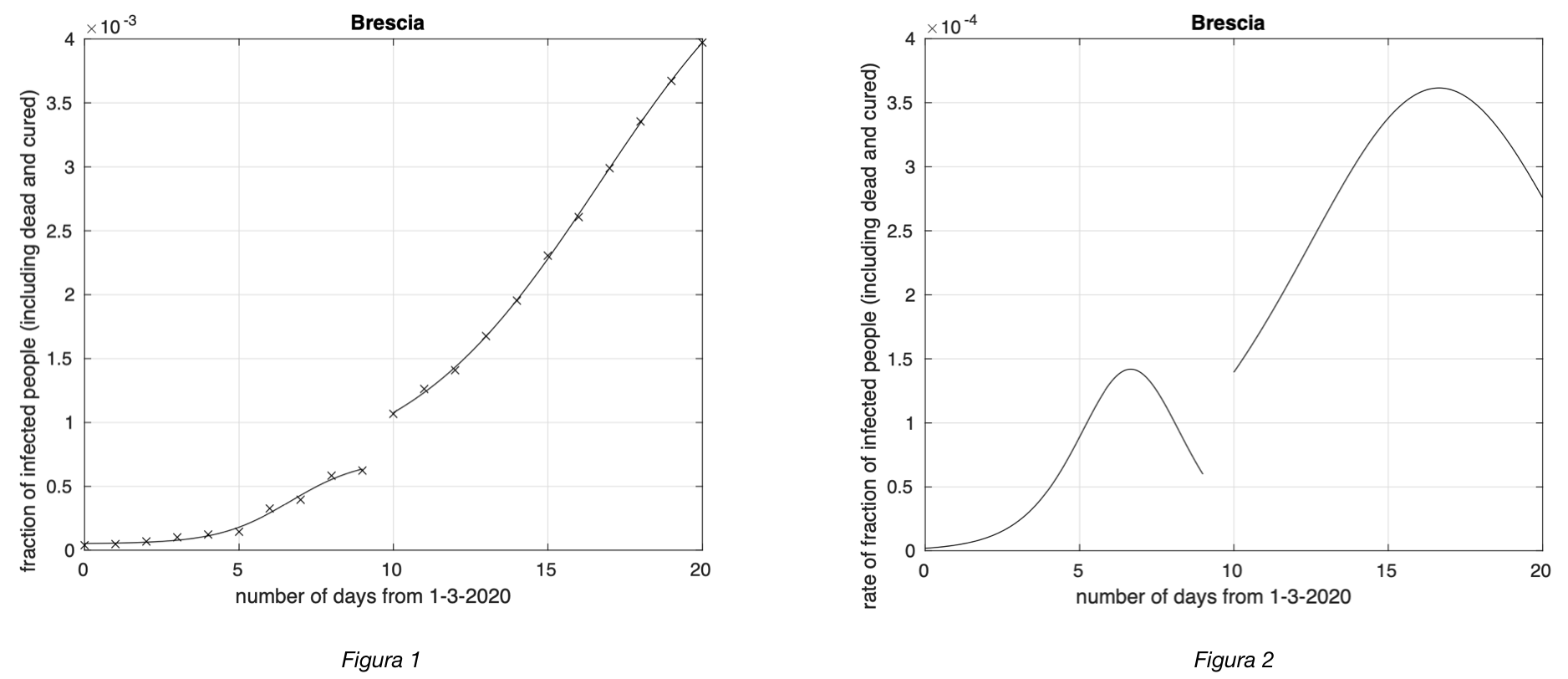 Notiamo che per 31 delle 107 province la curva della frazione dei contagiati osservati mostra un iniziale aumento del tasso crescita fino a raggiunngere un massimo per poi diminuire.
Notiamo che per 31 delle 107 province la curva della frazione dei contagiati osservati mostra un iniziale aumento del tasso crescita fino a raggiunngere un massimo per poi diminuire.
Improvvisamente verso l’11-12 marzo si ha successivamente un’inversione di tendenza e il tasso torna di nuovo a salire (vedi per esempio figure 1 e 2). Ipotizziamo che questo sia stato causato dall’impulso alla diffusione dell’epidemia dato dai fenomeni collettivi degli assalti ai treni e degli assalti ai supermercati avvenuti il 7-8 marzo in relazione al decreto che istituiva la zona rossa in Lombardia.
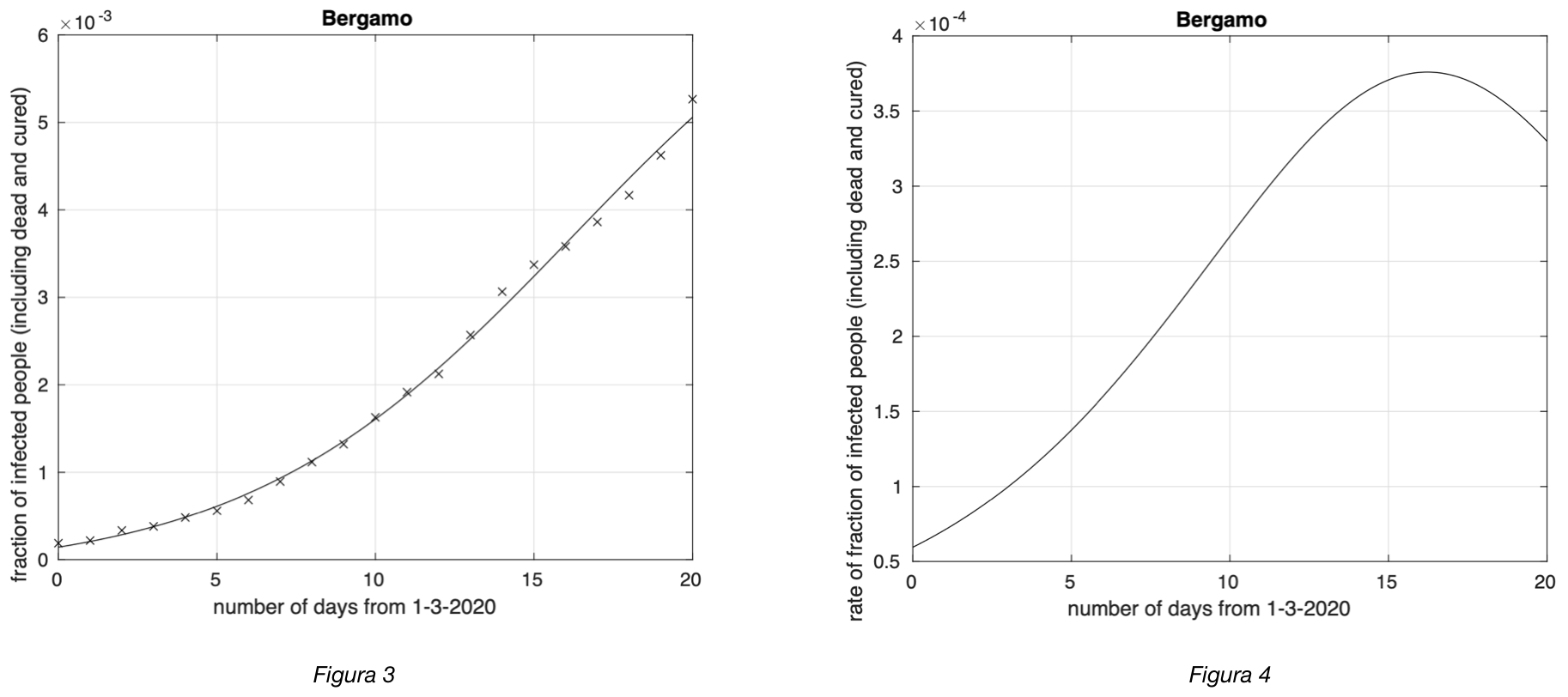 Per 64 delle 107 province i grafici mostrano evidenza di riduzione del tasso nella seconda parte dell’intervallo temporale (vedi per esempio figure 3 e 4). Ipotizziamo che questo sia stato causato dalla riduzione della diffusione indotta dalle misure di limitazione della mobilità introdotte col decreto “Io resto a casa” dell’11 marzo. Per le tre regioni maggiormente colpite, Lombardia, Emilia e Veneto, le province che mostrano questa diminuzione del tasso di crescita sono Bergamo, Brescia, Como, Cremona, Lodi, Monza, Pavia, Sondrio, Varese per la Lombardia, Piacenza, Parma, Reggio Emilia. Bologna, e Forlì Cesena per l’Emilia e Verona, Vicenza, Padova, Treviso per il Veneto. Per vedere i grafici di tutte le province, cliccare qui.
Per 64 delle 107 province i grafici mostrano evidenza di riduzione del tasso nella seconda parte dell’intervallo temporale (vedi per esempio figure 3 e 4). Ipotizziamo che questo sia stato causato dalla riduzione della diffusione indotta dalle misure di limitazione della mobilità introdotte col decreto “Io resto a casa” dell’11 marzo. Per le tre regioni maggiormente colpite, Lombardia, Emilia e Veneto, le province che mostrano questa diminuzione del tasso di crescita sono Bergamo, Brescia, Como, Cremona, Lodi, Monza, Pavia, Sondrio, Varese per la Lombardia, Piacenza, Parma, Reggio Emilia. Bologna, e Forlì Cesena per l’Emilia e Verona, Vicenza, Padova, Treviso per il Veneto. Per vedere i grafici di tutte le province, cliccare qui.
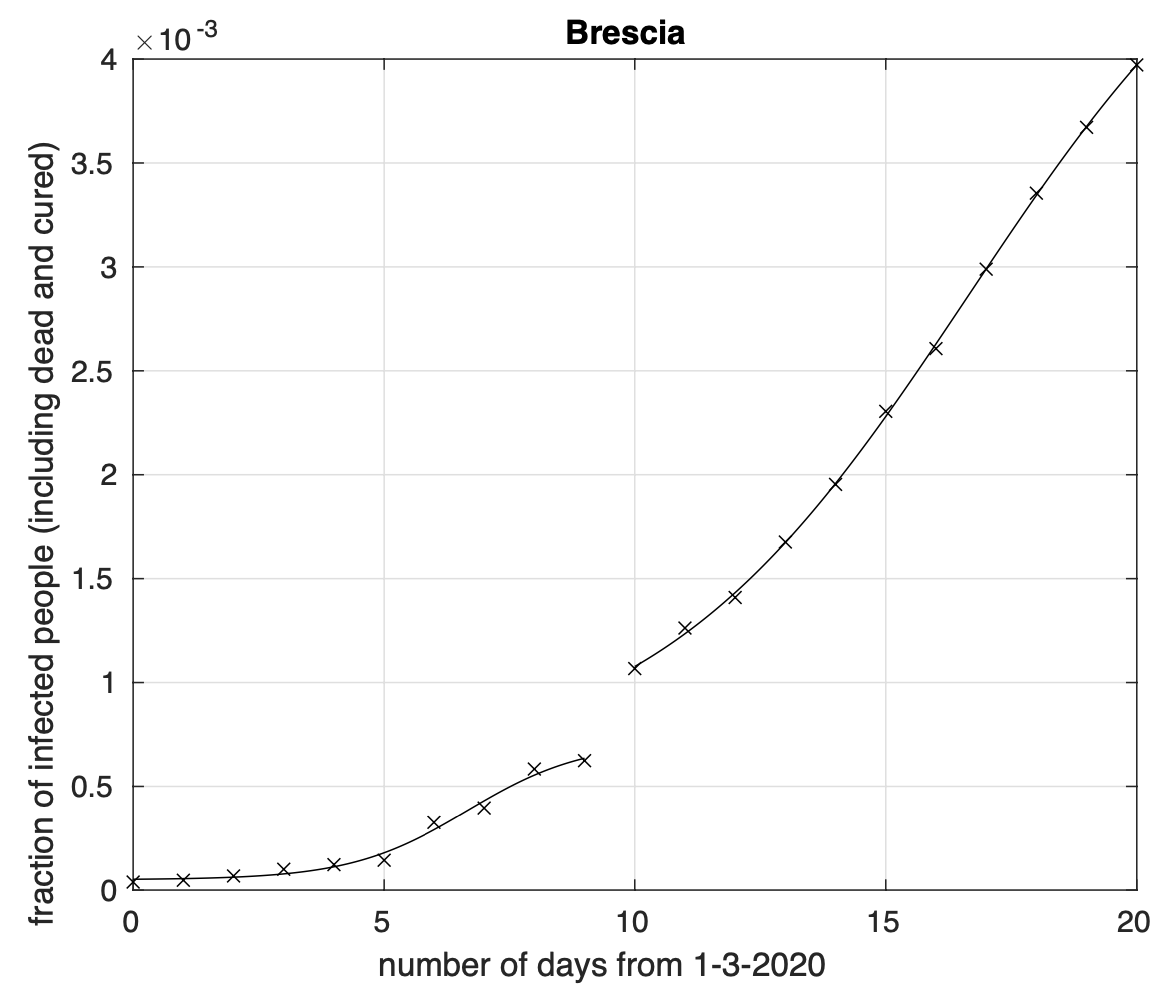
Figura 1. Frazione del numero di contagiati osservati nella provincia di Brescia rispetto alla popolazione della provincia in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati. Si osserva una fase in cui il tasso di crescita diminuisce. La curva della frazione dei contagiati, ossia coloro che sono al momento positivi al virus, o guariti o morti è per definizione crescente, o meglio "non decrescente". La rapidità con cui cresce la curva in un punto del tempo, il cosiddetto "tasso di crescita" si misura tramite la pendenza della retta tangente alla curva in quel punto. Più la pendenza è grande, più la curva cresce velocemente. Data una generica curva della frazione dei contagiati osservati al variare del tempo, possiamo costruire la curva che fornisce il tasso di crescita al variare del tempo. Quando il tasso inizia a diminuire la curva "flette", cioè cambia la sua concavità da verso l'alto a verso il basso e si appiattisce. Dopo un certo tempo, la curva non mostra più in pratica nessuna variazione.
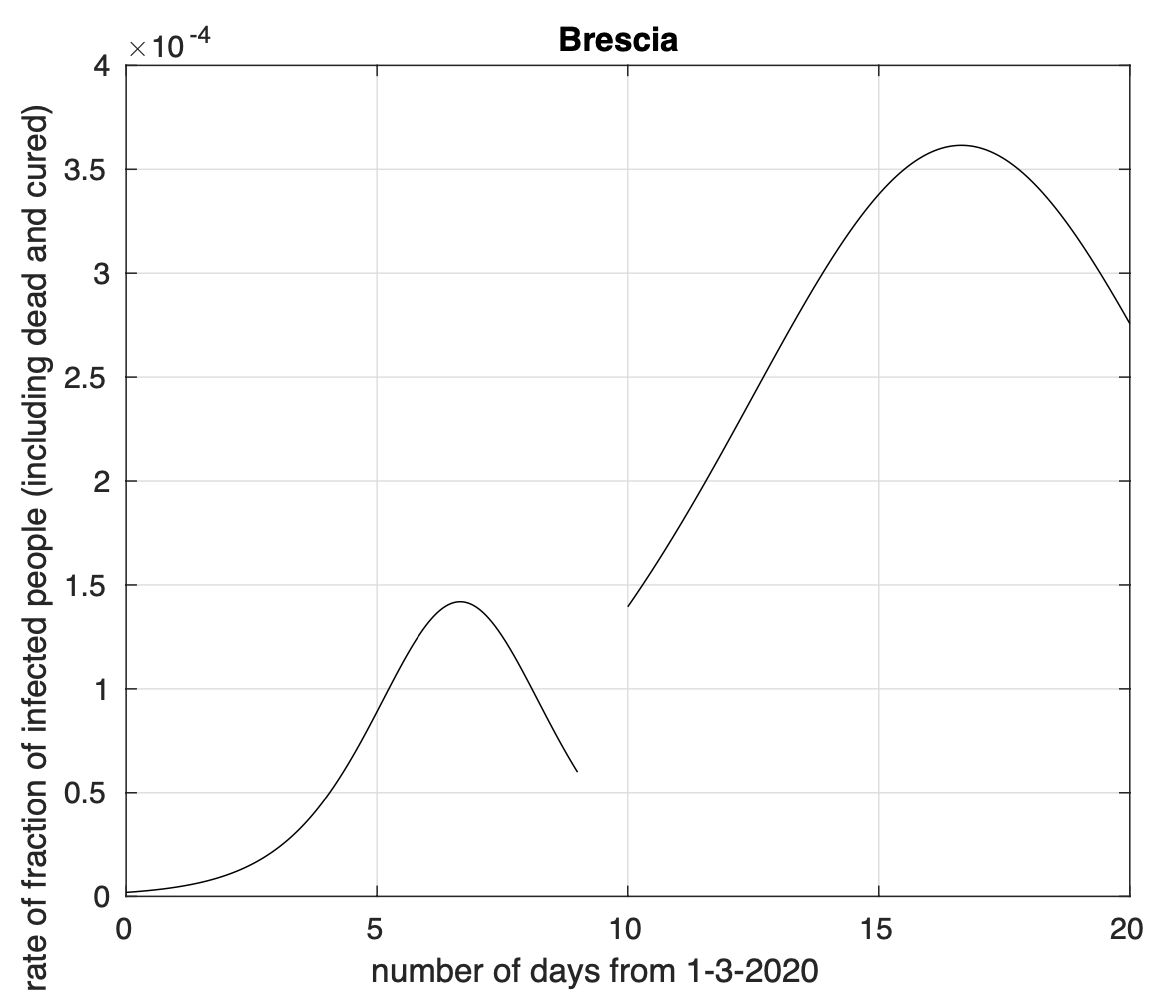
Figura 2. Tasso di crescita della frazione del numero di contagiati osservati a Brescia rispetto alla popolazione della provincia in funzione del tempo a partire dal 1 marzo. Il modello teorico adottato è quello logistico. Guardando la curva della frazione dei contagiati a Brescia, si vede che fino circa al 10 Marzo, l'andamento è quello "teorico" del fenomeno della diffusione dell'epidemia con la curva che diventa sempre più piatta. Poi, improvvisamente, attorno all'11 marzo si ha un'inversione di tendenza, la concavità torna di nuovo verso l'alto e il tasso torna a crescere.
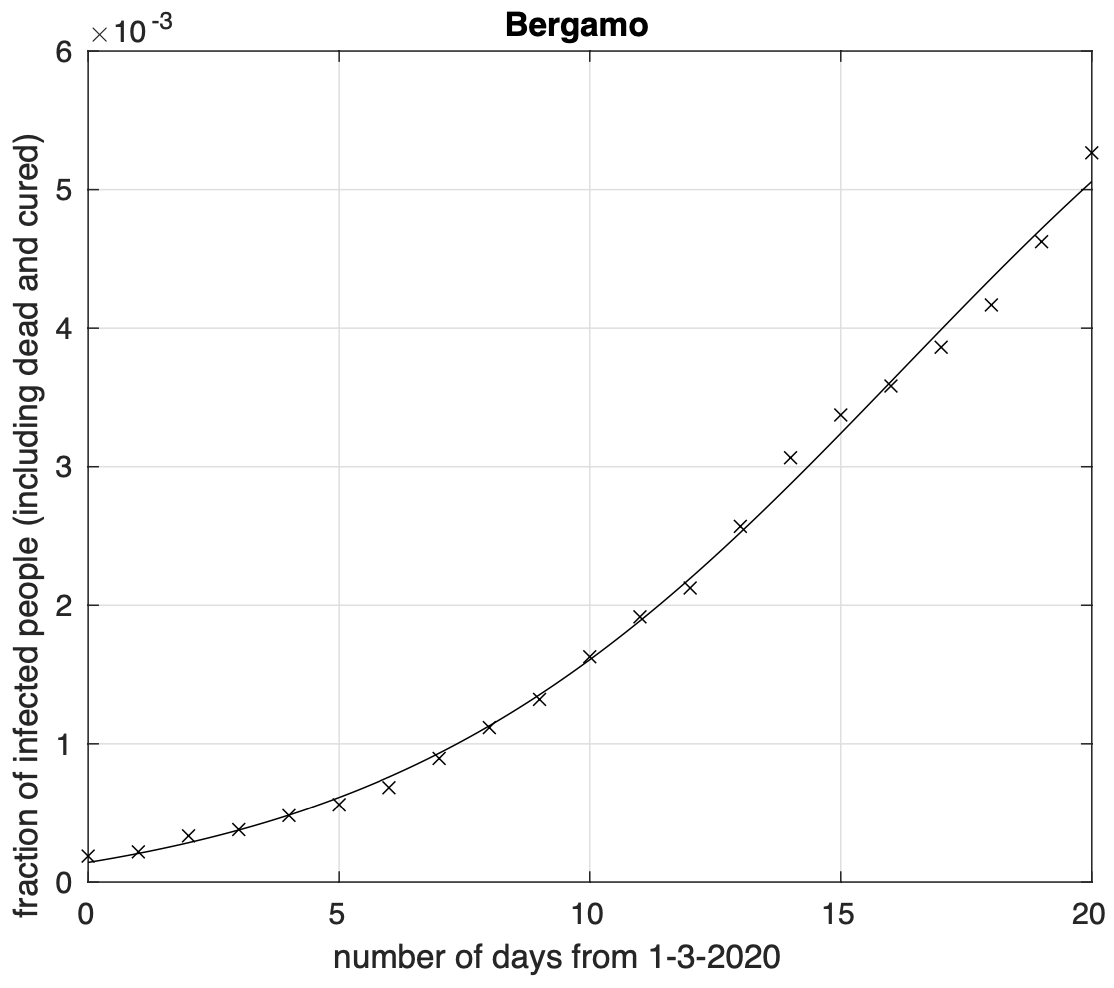
Figura 3. Frazione del numero di contagiati osservati nella provincia di Bergamo rispetto alla popolazione della provincia in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati. Si osserva una fase in cui il tasso di crescita diminuisce.
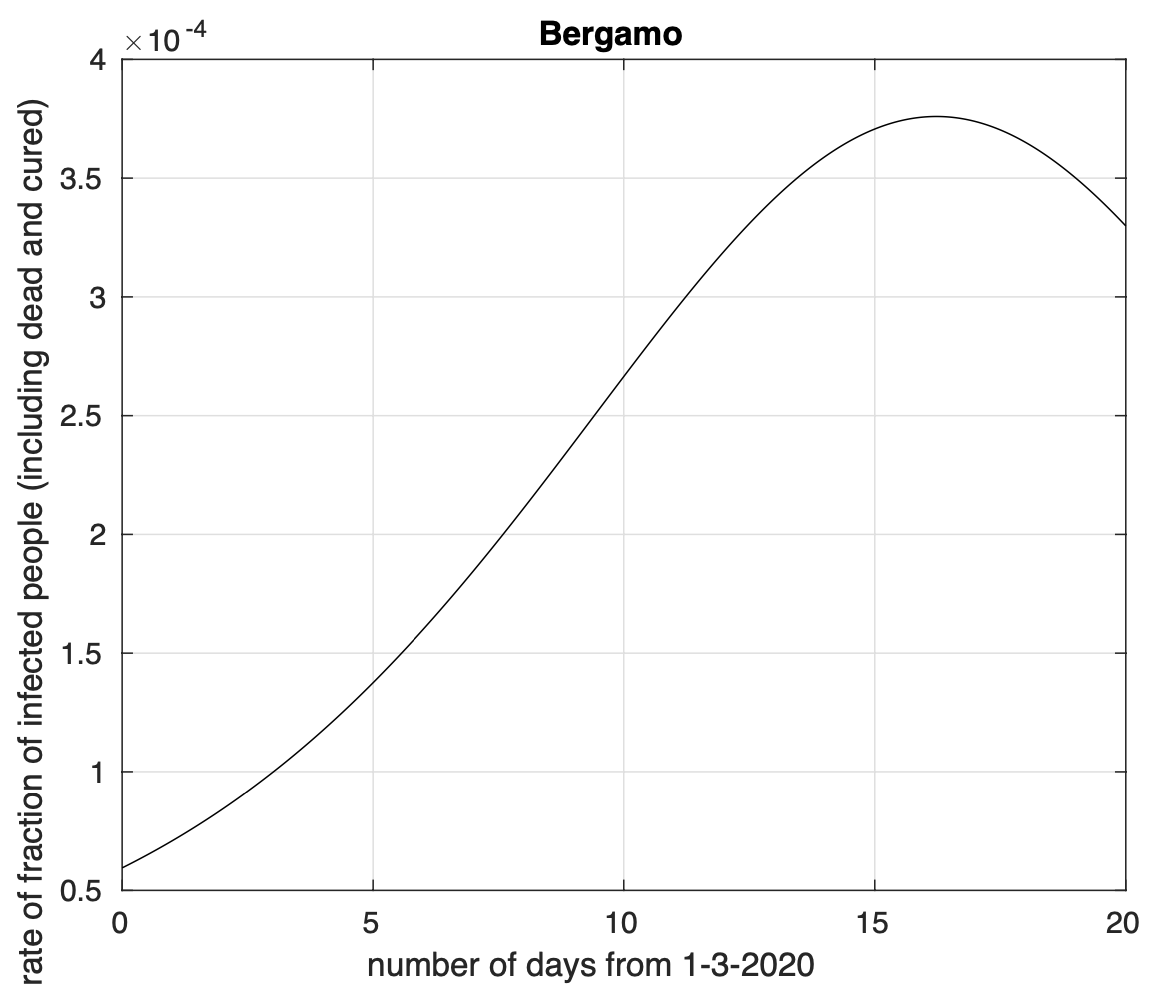
Figura 4. Tasso di crescita della frazione del numero di contagiati osservati a Bergamo rispetto alla popolazione della provincia in funzione del tempo a partire dal 1 marzo. Il modello teorico adottato è quello logistico.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
Analisi dei dati epidemiologici del coronavirus in Italia (al 20 marzo)
- 8426 letture
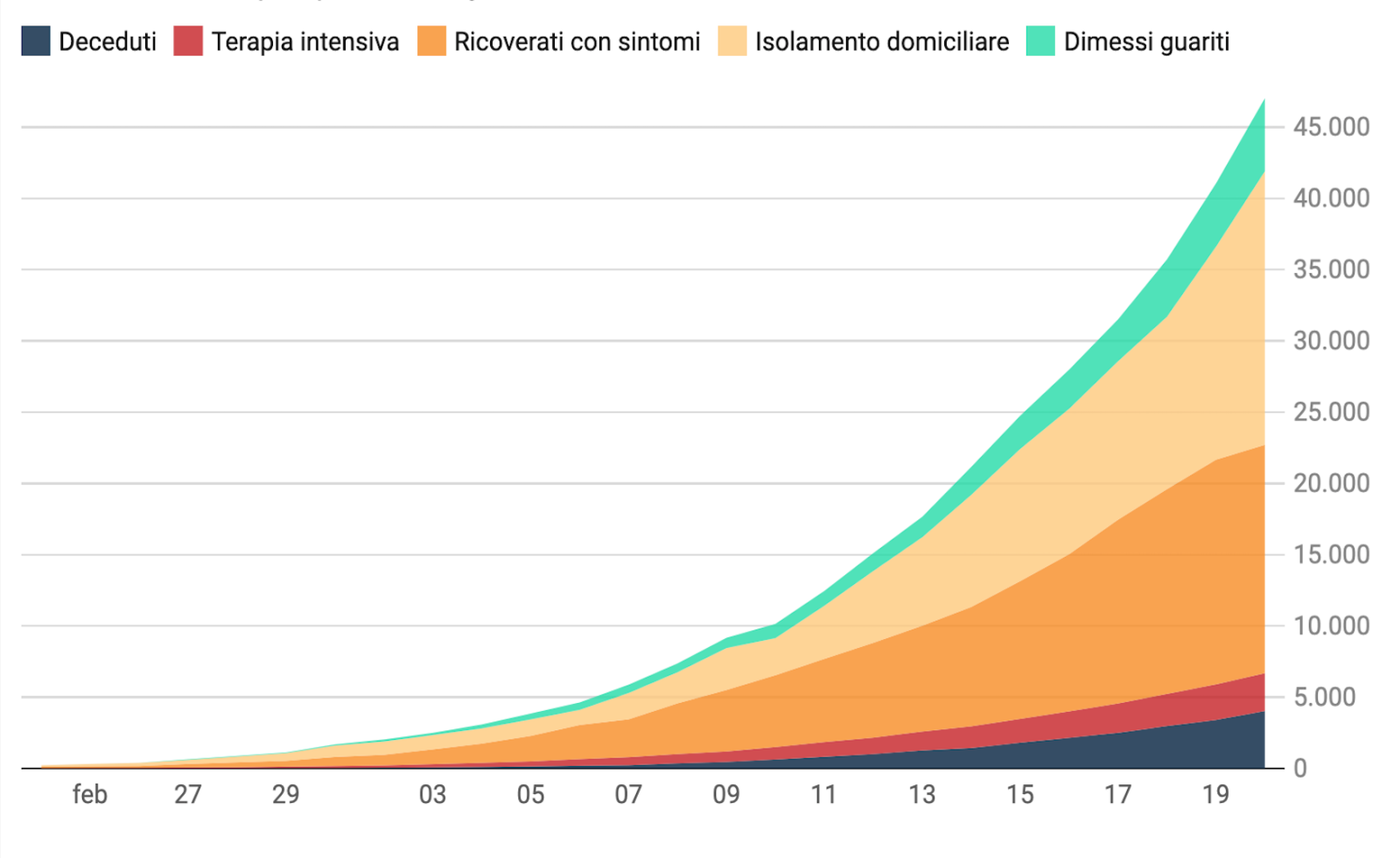
In questo documento sono descritti i risultati relativi all’analisi per le province al momento maggiormente colpite di ciascuna regione, escluse quelle di Molise e Basilicata a causa del loro basso numeri di casi. I risultati sostituiscono o integrano quelli nel documento del 19 marzo. I dati utilizzati sono quelli aggiornati alle 18 del 20 marzo 2020 e sono stati scaricati dal sito https://github.com/pcm-dpc/COVID-19/tree/master/dati-province.
Alla luce delle osservazioni del documento del 19 marzo, non abbiamo effettuato analisi a livello regionale, ma solo a livello provinciale, dove sussistono probabilmente condizioni di maggior omogeneità dei fattori che influenzano il fenomeno di diffusione del virus. Alcune caratteristiche delle curve delle diverse province potrebbero scomparire cumulando le curve per ottenere quella a livello regionale.
Il modello teorico adottato per descrivere i dati è quello logistico. Per alcune province, abbiamo utilizzato un modello con due o tre funzioni logistiche in sequenza allo scopo di modellizzare l’eventuale presenza di fasi consecutive in ciascuna delle quali si osserva un’iniziale aumento del tasso di crescita della frazione dei contagiati, seguito da una sua diminuzione.
Osserviamo che circa la metà delle province considerate presenta una riduzione del tasso di crescita, che a livello della curva della frazione dei contagiati osservati, si traduce nel famoso “appiattimento della curva” del quale si parla tanto. Come detto in precedenza, ci aspettiamo che tale riduzione sia progressiva (se non intervengono altri fenomeni collettivi) e che sia dovuta all’introduzione delle misure restrittive sulla mobilità introdotte l’11 marzo. La presenza degli errori nei dati sperimentali e il fatto che siamo solo nella parte iniziale della fase di diminuizione del tasso di crescita, può indurre variazioni grandi sui valori stimati per i parametri del modello. Di conseguenza è possibile che un dato caso presenti un certo giorno evidenza sperimentale che ci troviamo nella fase di dimuzione del tasso di crescita, mentre il giorno successivo questo non accade. La conferma di tale evidenza nei giorni successivi aumenta la veromiglianza che ci si trovi davvero in una fase di riduzione del tasso. Nella figura 1 possiamo vedere l’andamento nel tempo della frazione del numero di contagiati osservati rispetto alla popolazione della provincia, con sovrapposto il modello logistico che meglio si adatta ai dati. Nella figura 2 viene rappresentato nel tempo il tasso di crescita corrispondente al modello stimato. Si osserva da questa figura che il tasso di crescita ha iniziato a scendere. Nelle altre figure, sono mostrati i risultati per tutte le altre province considerate: scarica il pdf con i grafici per tutte le province.
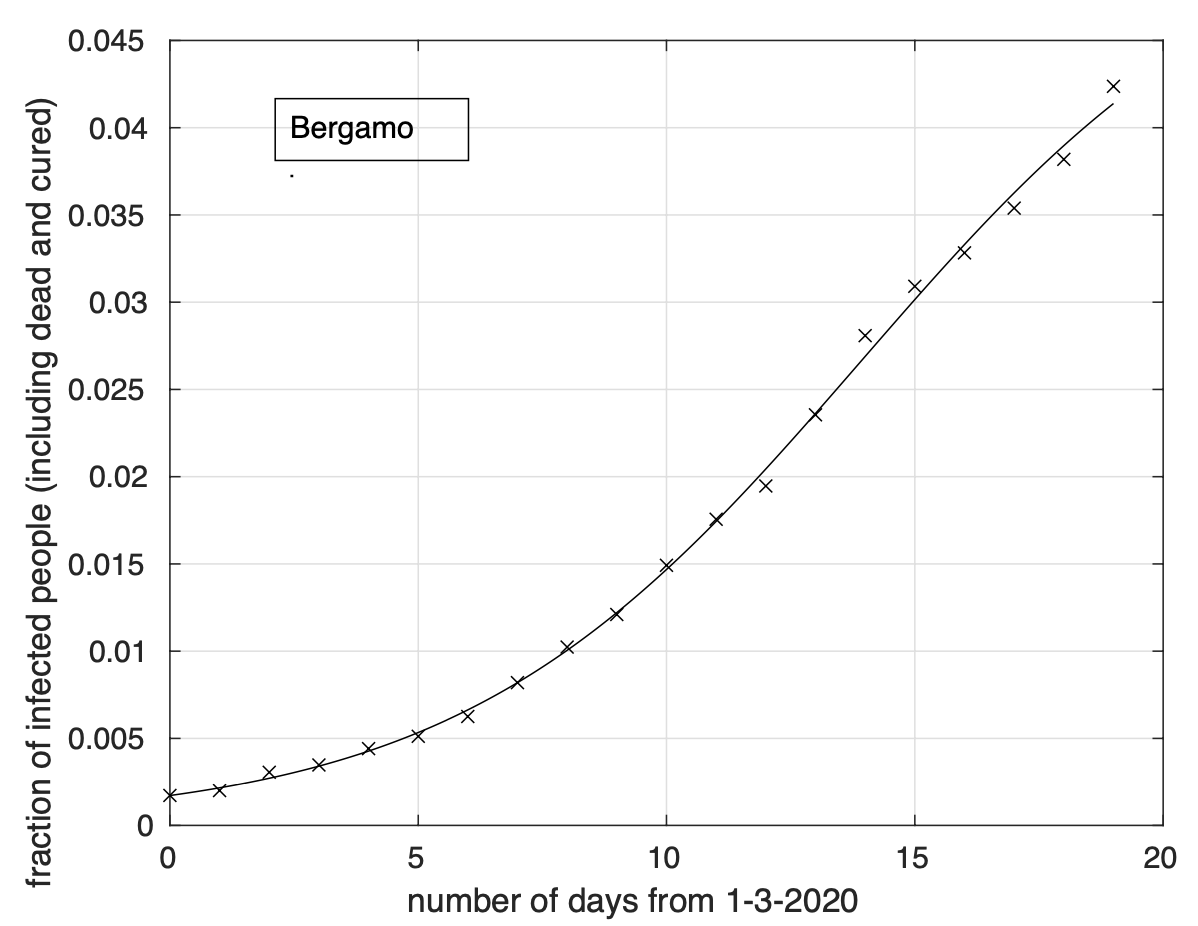
Figura 1. Frazione del numero di contagiati osservati nella provincia di Bergamo rispetto alla popolazione della provincia in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati. Si osserva una fase in cui il tasso di crescita diminuisce.
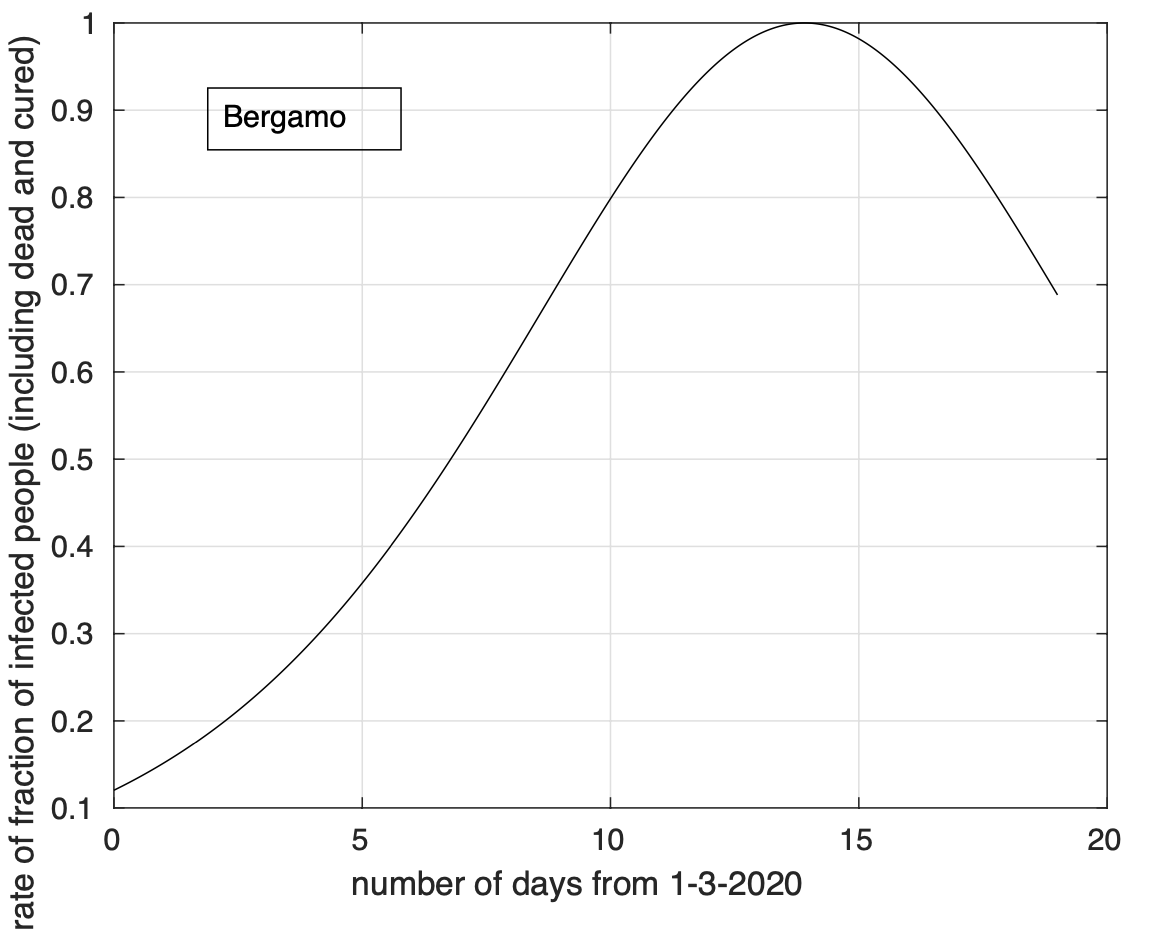
Figura 2. Tasso di crescita della frazione del numero di contagiati osservati a Bergamo rispetto alla popolazione della provincia in funzione del tempo a partire dal 1 marzo. Il modello teorico adottato è quello logistico.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
Analisi dei dati epidemiologici del coronavirus in Italia (al 19 marzo)
- 11484 letture
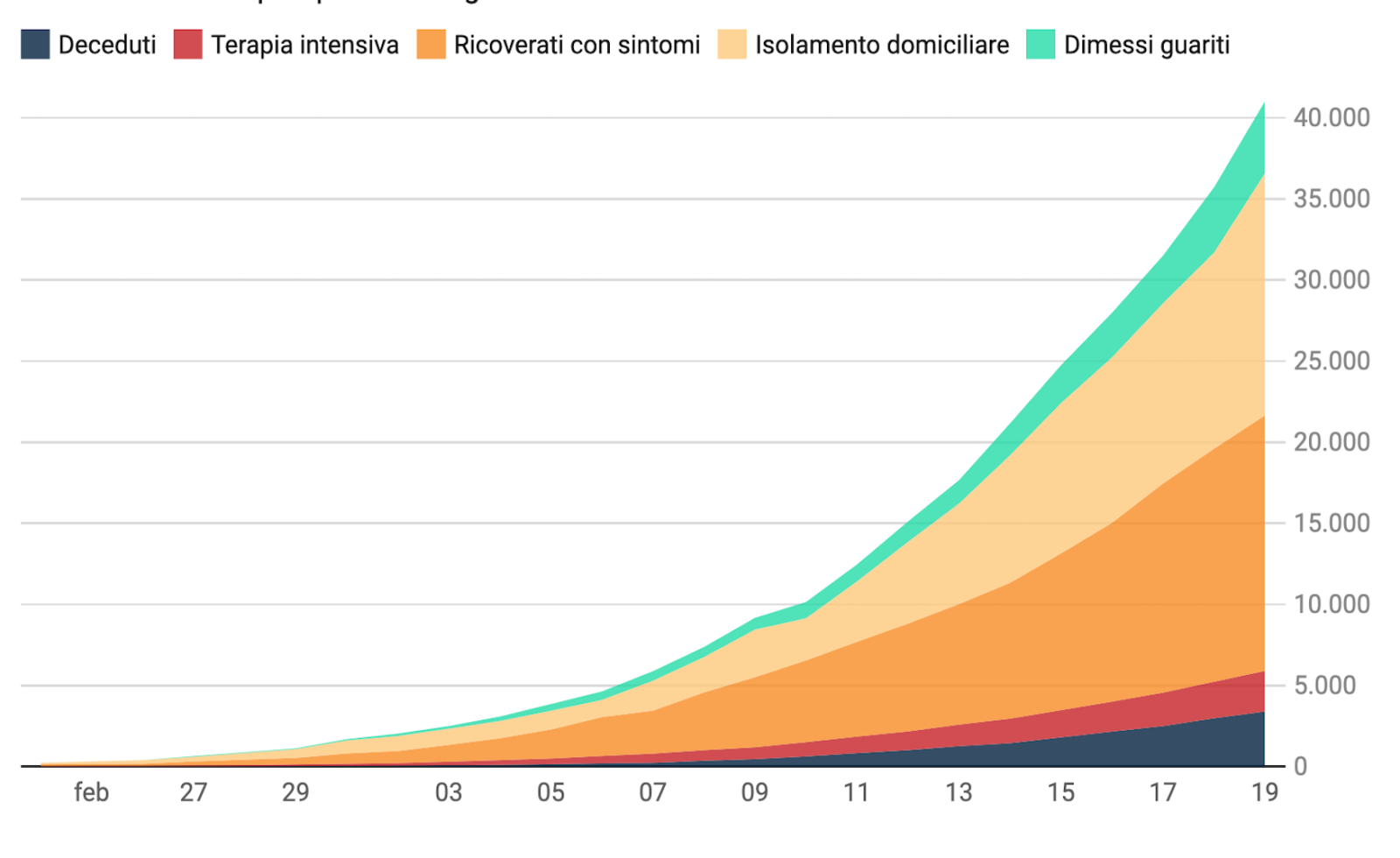
In questo documento sono descritti i risultati relativi all’analisi per le tre regioni maggiormente colpite, Lombardia, Emilia e Veneto, per le sei province della Lombardia al momento maggiormente colpite, per la provincia più colpita dell’Emilia e quella più colpita del Veneto. I dati utilizzati sono quelli aggiornati alle 18 del 19 marzo 2020, che sostituiscono o integrano quelli nel documento del 18 marzo. I dati a livello regionale sono stati scaricati dal sito https://github.com/pcm-dpc/COVID-19 e quelli a livello provinciale dal sito https://github.com/pcm-dpc/COVID-19/tree/master/dati-province.
Per quanto riguarda la Lombardia, si conferma anche per il 19 marzo la piccola ma progressiva riduzione del tasso di crescita della frazione dei contagiati osservati relativa ai giorni precedenti, come si può osservare nella figura 1 e in modo più evidente nella figura 2 che rappresenta, in funzione del tempo, proprio il tasso di crescita stimato a partire dai dati. Come detto in precedenza, ci aspettiamo che tale riduzione sia progressiva (se non intervengono altri fenomeni collettivi) e che sia dovuta all’introduzione delle misure restrittive sulla mobilità introdotte l’11 marzo. Rimandiamo ai prossimi sette giorni la verifica di questa ipotesi. Analoga situazione per il Veneto, come si può osservare nelle analoghe figure 3 e 4. Diverso è invece il comportamento dell’Emilia dove, con i dati disponibili fino ad oggi, non c’è evidenza di riduzione del tasso di crescita (vedi figure 5 e 6). Questo accade anche se adottiamo un modello più accurato di quello logistico come quello doppio logistico, come si osserva nelle figure 7 e 8.
A livello provinciale, per cinque delle sei province attualmente maggiormente colpite della Lombardia, Bergamo, Brescia, Cremona, Lodi, Milano, osserviamo una diminuzione del tasso di crescita, con delle differenze tra provincia e provincia, come mostrano le figure 9 e 10 per Bergamo e Brescia, rispettivamente. Per Milano (vedi figura 11) non c’è al momento evidenza di riduzione del tasso. In figura 12 possiamo vedere che per Lodi il tasso di crescita diminuisce costantemente sin da subito. Sarebbe quindi utile studiare nel dettaglio questo caso per capire da cosa dipenda questo comportamento peculiare indentificando eventualmente le principali cause, auspicando che siano legate ad alcune delle misure adottate per fronteggiare l’emergenza e al comportamento della popolazione.
Nella figura 13 vediamo il risultato per la provincia di Padova. Analogamente a quello che accade a livello regionale, anche per questa provincia si nota una riduzione del tasso di crescita. Come abbiamo visto dalle figure 5-8, per l’Emilia non osserviamo una riduzione del tasso. Dalla figura 14 possiamo invece vedere che la provincia di Piacenza mostra una riduzione del tasso di crescita, probabilmente determinata, come per gli altri casi, dall’introduzione delle misure di restrizione della mobilità col decreto “Io resto a casa” dell’11 marzo. Questo fatto suggerisce di effettuare le analisi su scale territoriali piccole, come per esempio quella provinciale, dove sussistono probabilmente condizioni di maggior omogeneità dei fattori che influenzano il fenomeno di diffusione del virus. Alcune caratteristiche delle curve delle diverse province potrebbero scomparire cumulando le curve per ottenere quella a livello regionale.
Ci rendiamo conto che ci sono dei problemi legati ai dati misurati, specialmente in questo periodo dove in alcune povince la situazione negli ospedali è molto critica a causa dell’elevato numero di pazienti e della carenza di risorse umane a disposizione. Infatti alcuni medici e infermieri sono stati contagiati dal virus e si sono ammalati. Tra le variabili considerate, il numero dei morti presenta anche la difficoltà legata alla sua definizione. Alcuni criticano l’inclusione nel computo dei morti di quelle persone morte e positive al test che presentavano co-morbilità, tipicamente di età avanzata, poiché pensano che sarebbero morte comunque in breve tempo. Questo spiegherebbe almeno in parte l’elevato tasso di mortalità in Italia se confrontato con quello della Cina ad esempio. Si dovrebbe a mio avviso innanzi tutto fare il tampone a tutte le persone morte, cosa che non accade. Questo comunque è comprensibile in una situazione di grande difficoltà a gestire un elevato numero di pazienti. Nel caso di morte con tampone positivo, si potrebbe attribuire la morte al coronavirus se vale almeno una delle due condizioni:
- il tempo tra la diagnosi o l’inizio della fase di peggioramento e la morte è significativamente più piccolo dell’aspettativa di vita della categoria a cui appartiene quel determinato paziente;
- la morte è avvenuta in seguito a complicazioni caratteristiche della malattia indotta dal coronavirus, tipicamente la polmonite.
In questo modo non risolveremmo tutti i casi, ma sarebbe molto meglio che considerare morti per il coronavirus tutti i positivi al test o in alternativa solo i soggetti senza co-morbilità. Vale comunque l’affermazione di prima circa la scala di priorità in una fase di emergenza come quella attuale nelle province più colpite. Inoltre penso che il confronto della mortalità tra situazioni diverse, come il caso cinese e quello italiano, ha senso solo alla fine dell’epidemia e non durante il suo sviluppo a causa del ritardo delle morti. Infine, il tasso di morte potrebbe essere sovrastimato anche a causa della sottostima del numero di contagiati in relazione alla presenza dei portatori sani, dei quali ignoriamo il numero.

Figura 1. Frazione del numero di contagiati osservati in Lombardia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati.
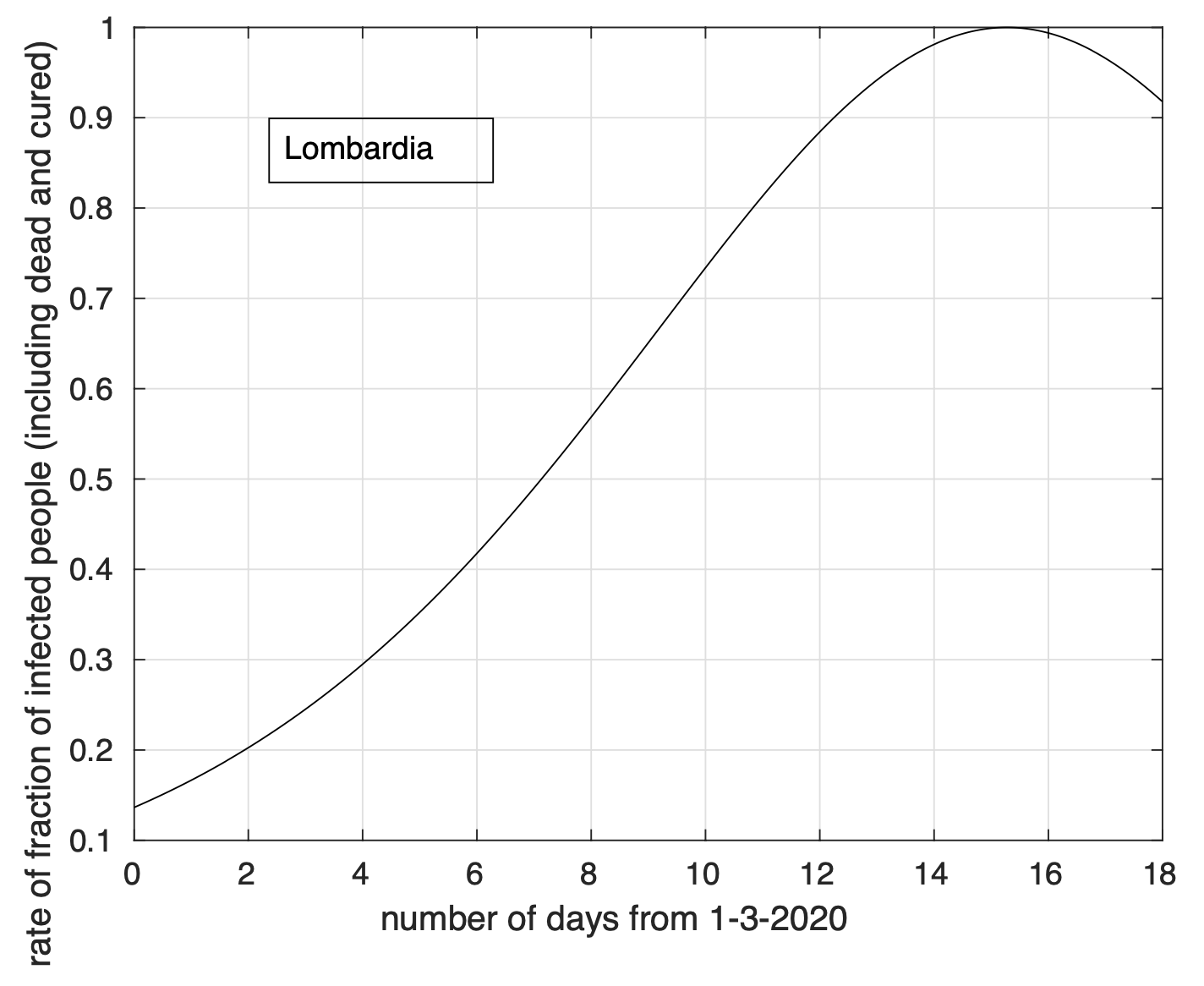
Figura 2. Tasso di crescita della frazione del numero di contagiati osservati in Lombardia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. La curva rappresentata è la derivata del modello teorico sovrapposto ai dati in figura 1.

Figura 3. Frazione del numero di contagiati osservati nel Veneto rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati.

Figura 4. Tasso di crescita della frazione del numero di contagiati osservati in Veneto rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il modello teorico adottato è quello logistico.
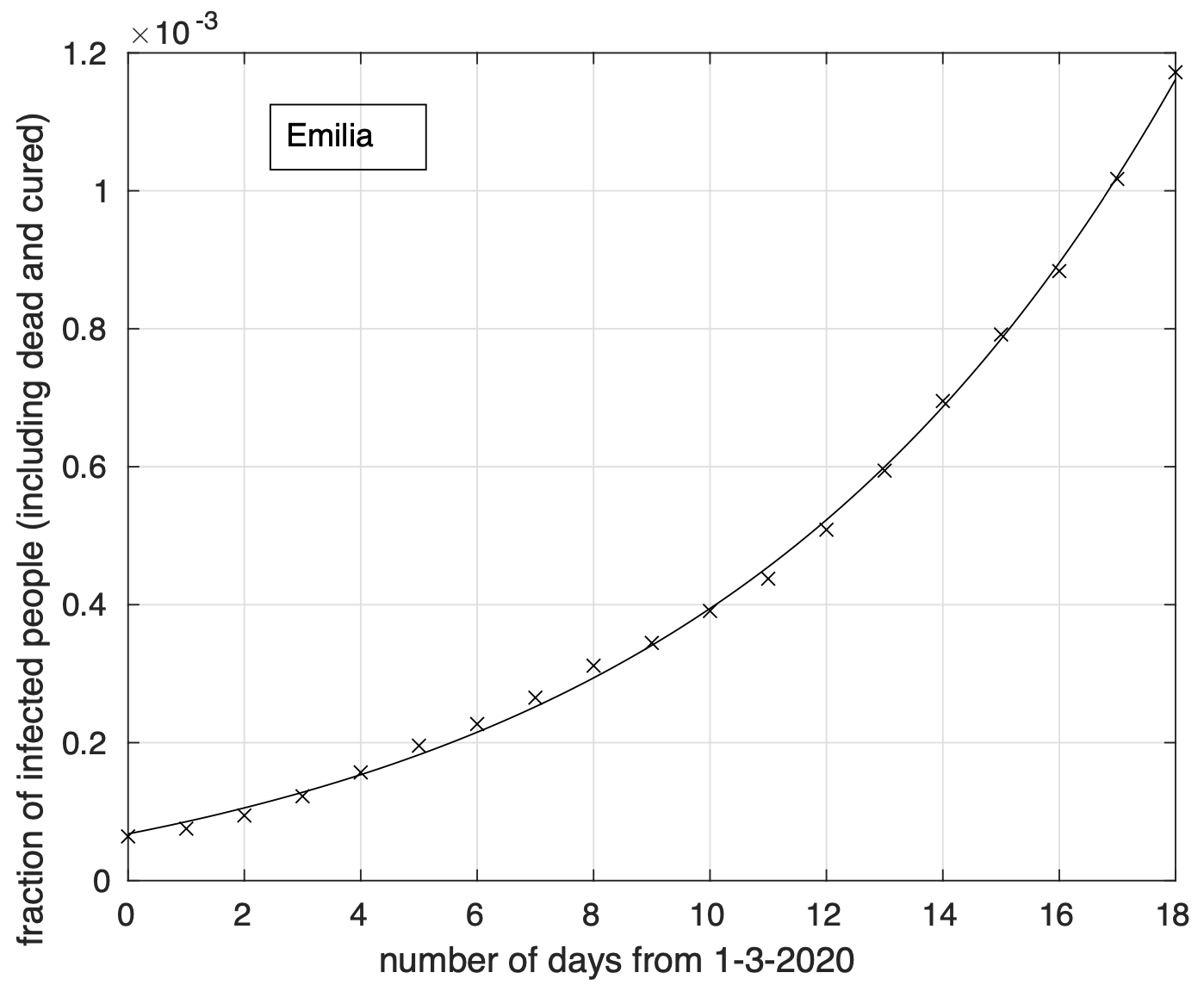
Figura 5. Frazione del numero di contagiati osservati in Emilia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati.
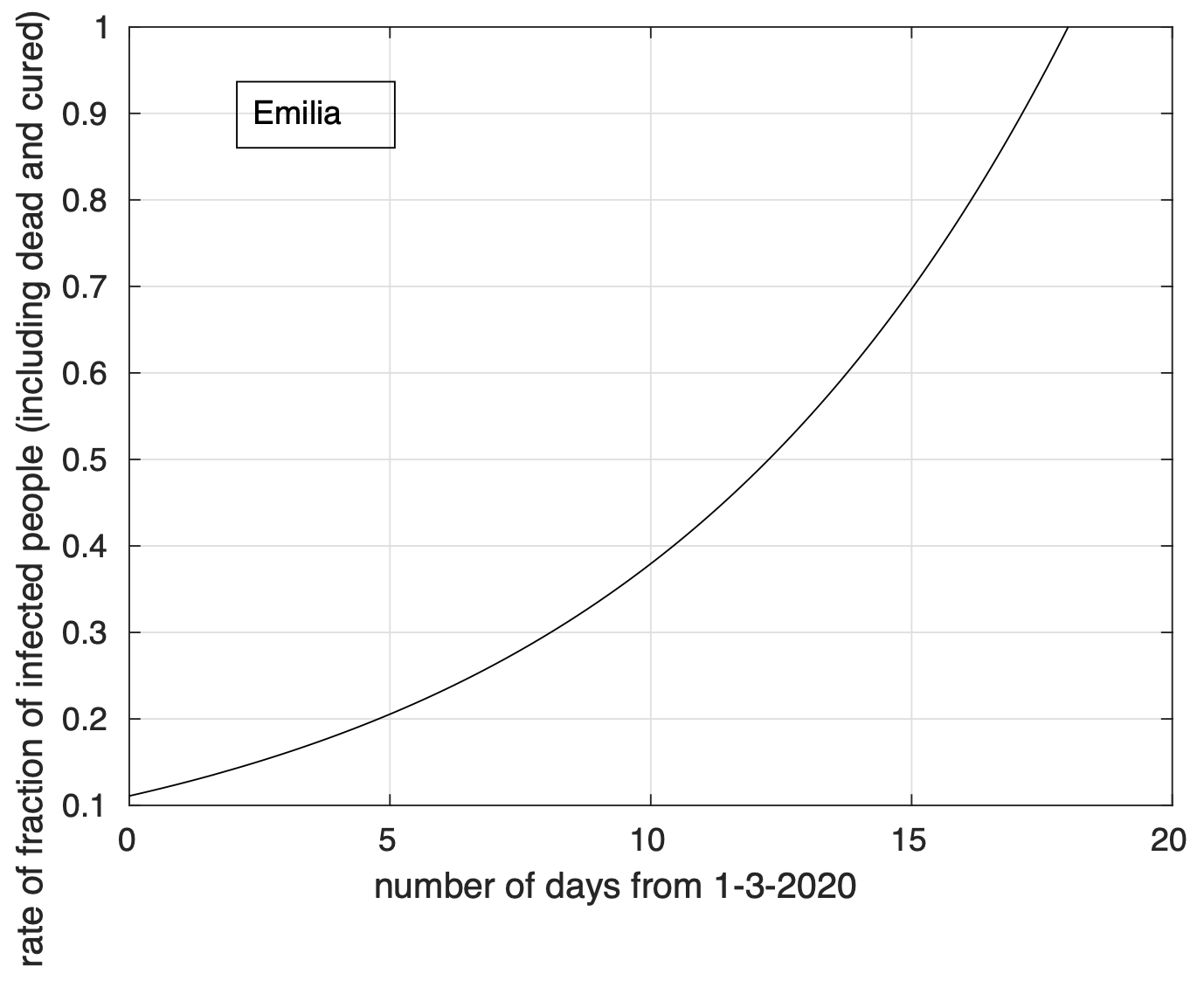
Figura 6. Tasso di crescita della frazione del numero di contagiati osservati in Emilia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il modello teorico adottato è quello logistico.
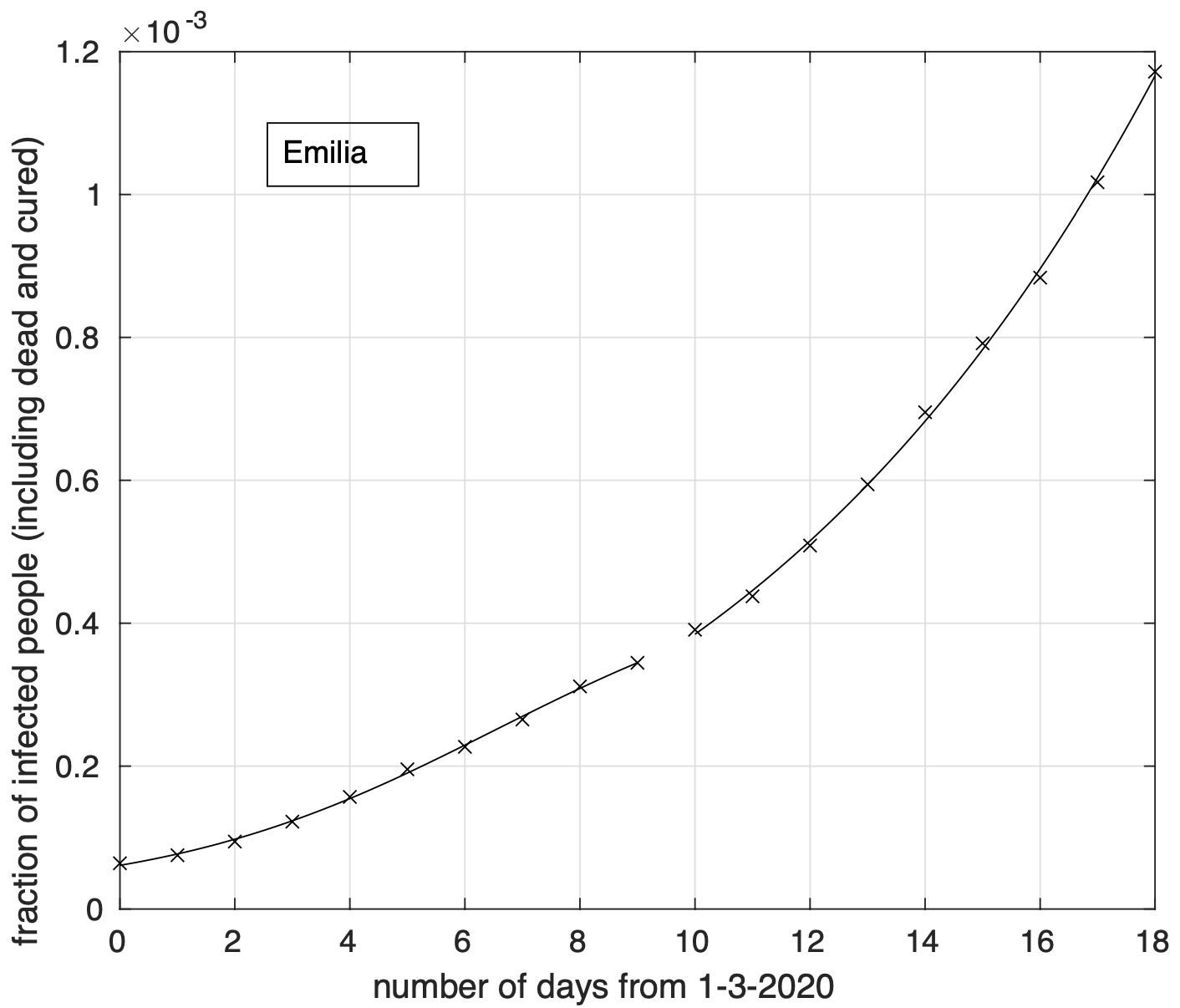
Figura 7. Frazione del numero di contagiati osservati in Emilia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello doppio logistico è sovrapposto ai dati.
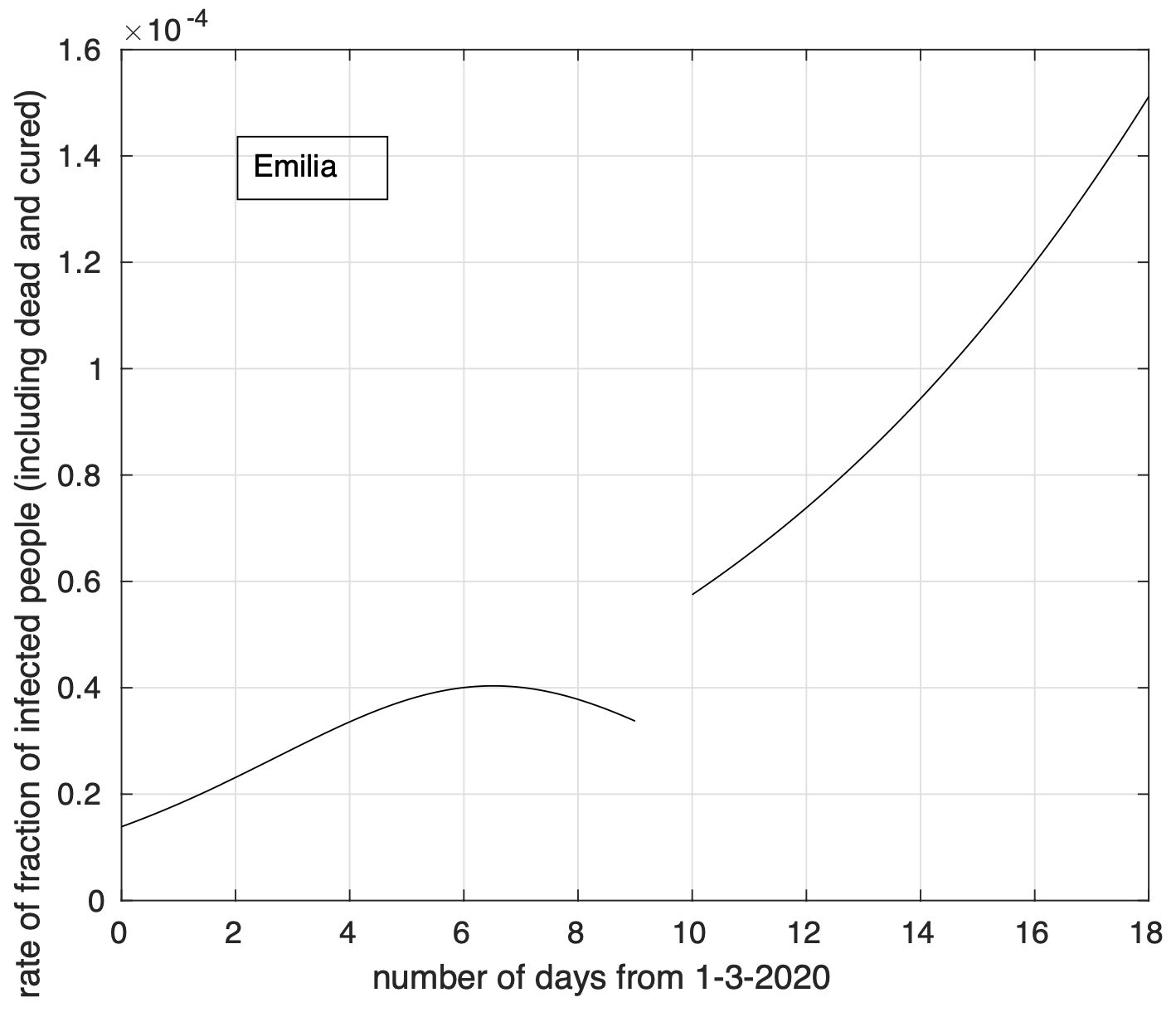
Figura 8. Tasso di crescita della frazione del numero di contagiati osservati in Emilia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il modello teorico adottato è quello doppio logistico.
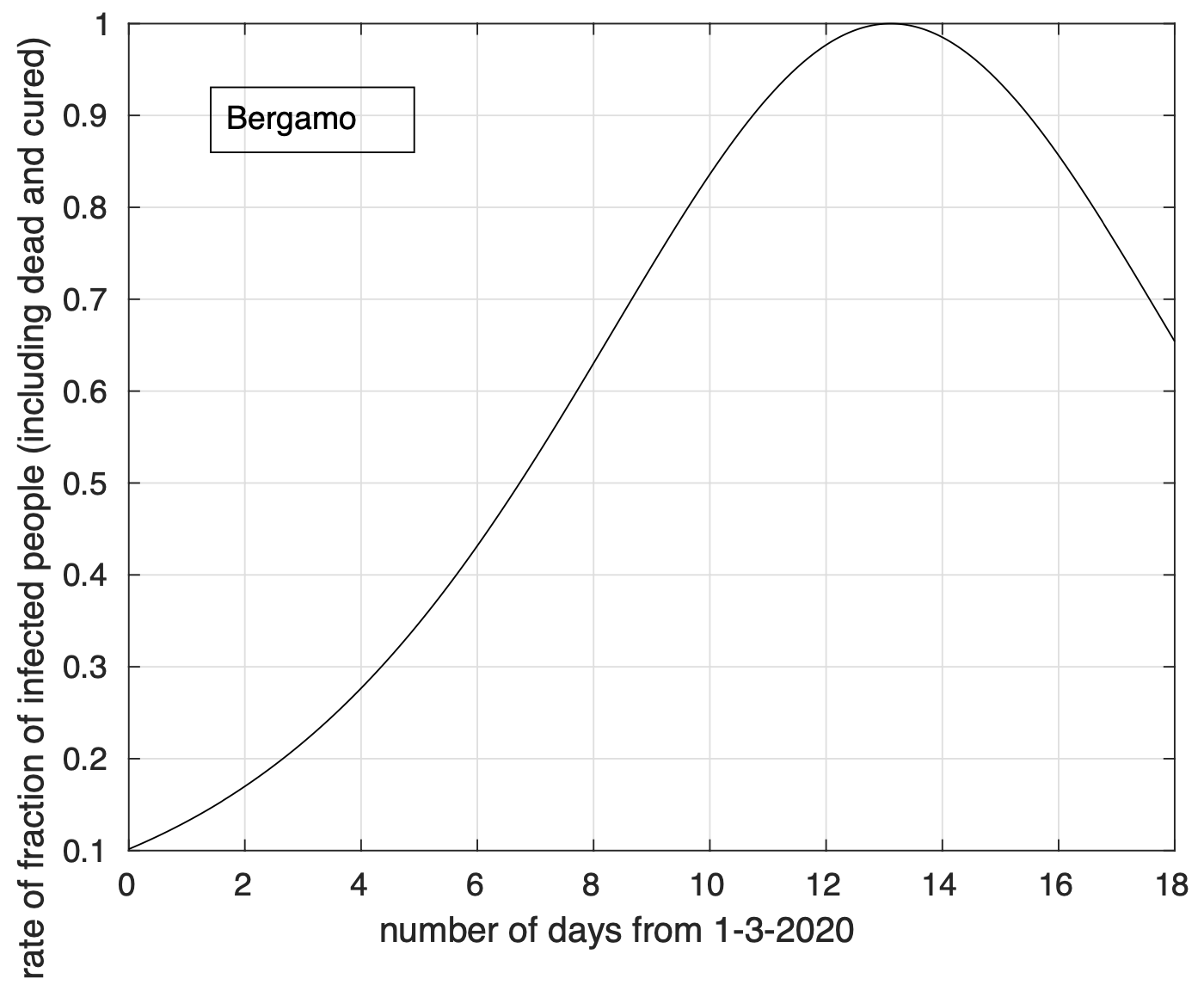
Figura 9. Tasso di crescita della frazione del numero di contagiati osservati a Bergamo rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il modello teorico adottato è quello logistico.
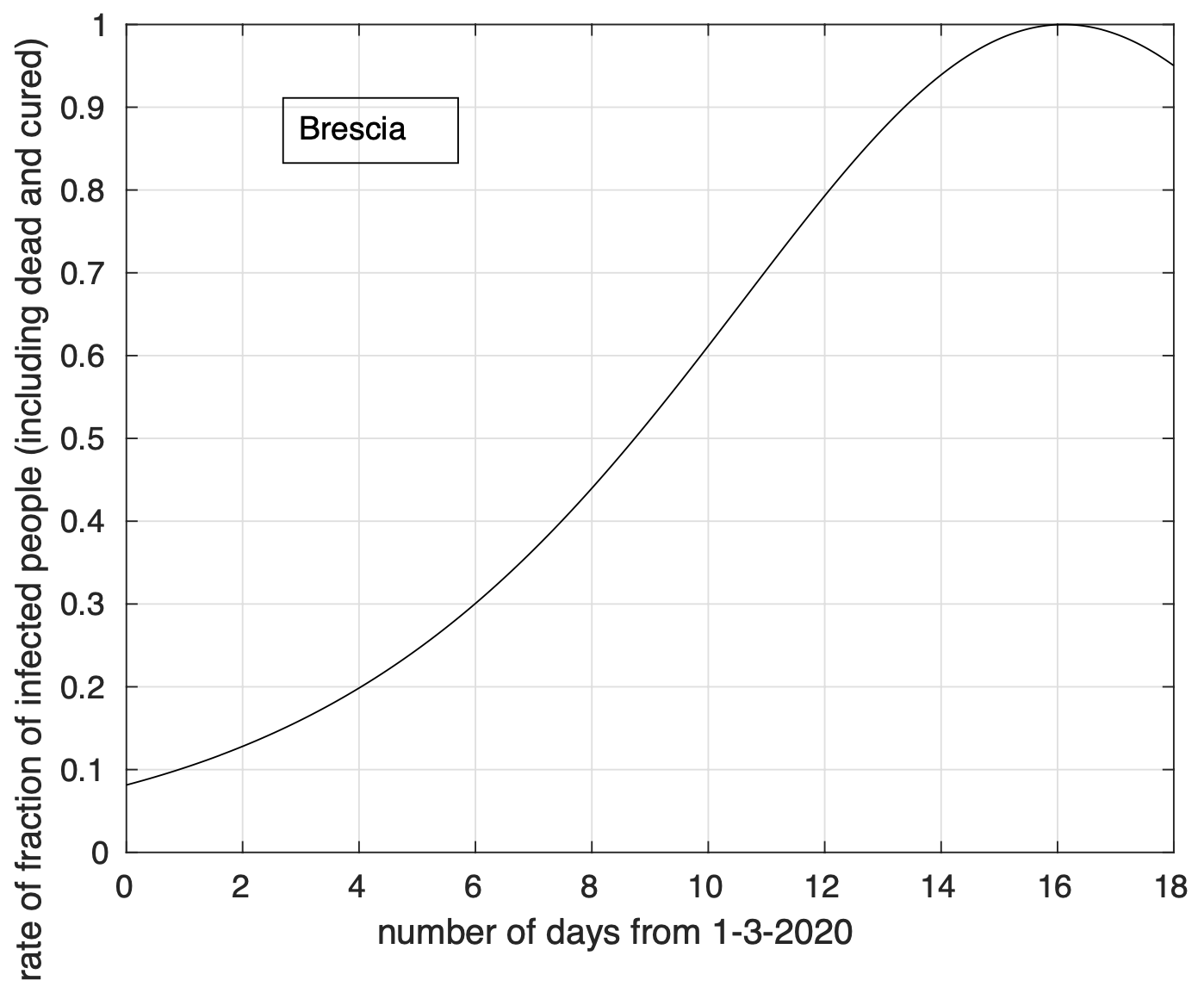
Figura 10. Tasso di crescita della frazione del numero di contagiati osservati a Brescia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il modello teorico adottato è quello logistico.
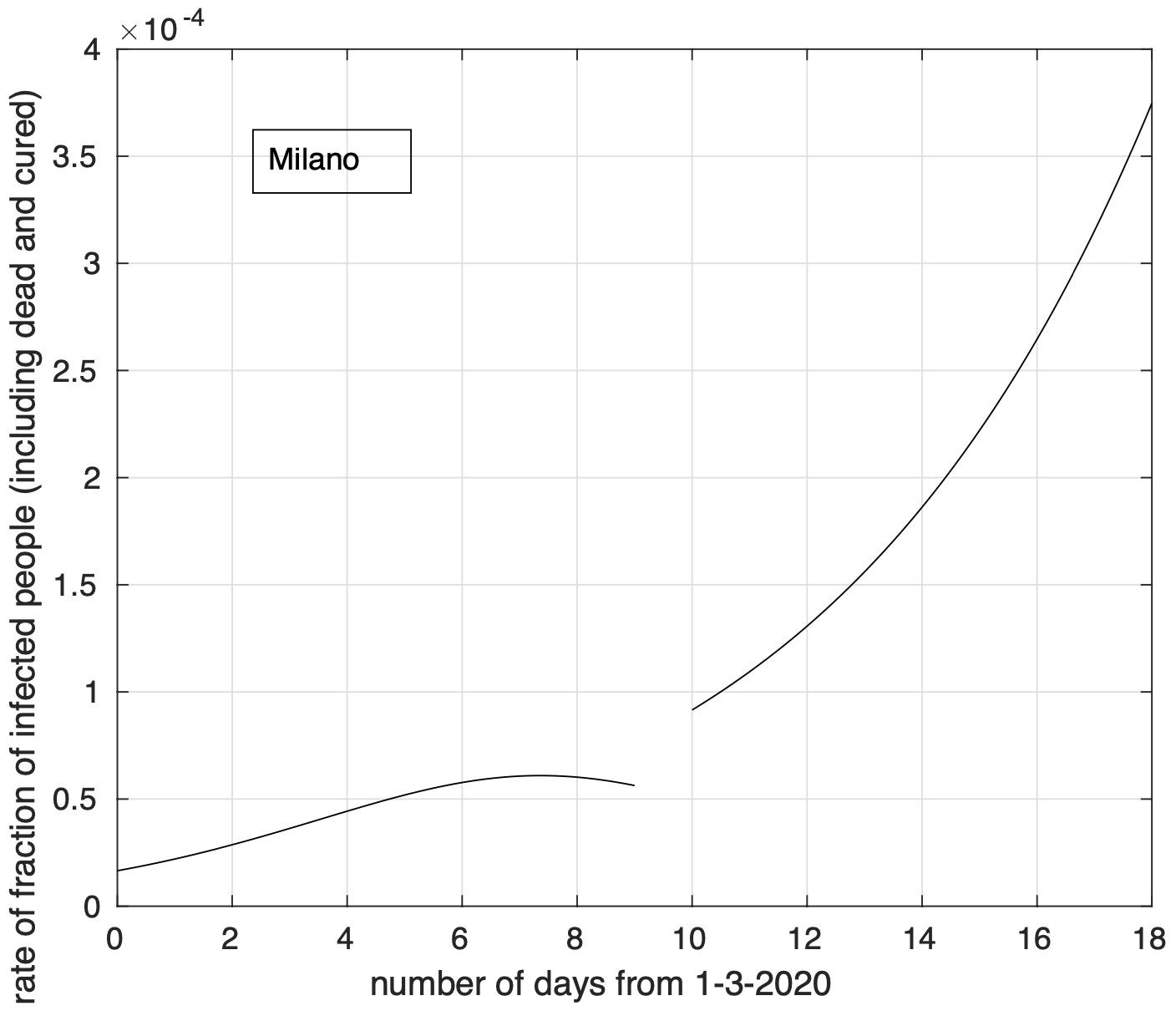
Figura 11. Tasso di crescita della frazione del numero di contagiati osservati a Milano rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il modello teorico adottato è quello doppio logistico.
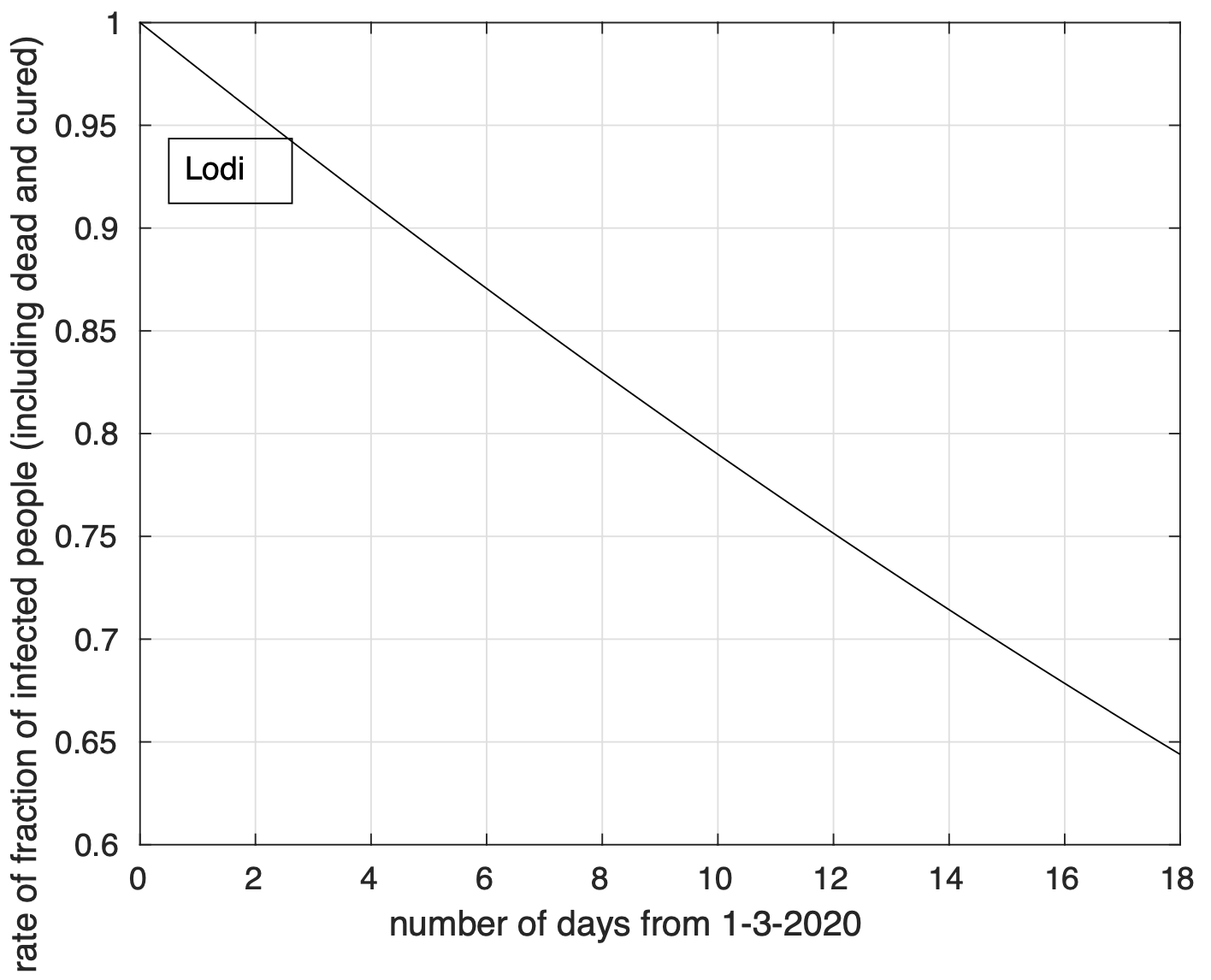
Figura 12. Tasso di crescita della frazione del numero di contagiati osservati a Lodi rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il modello teorico adottato è quello logistico.
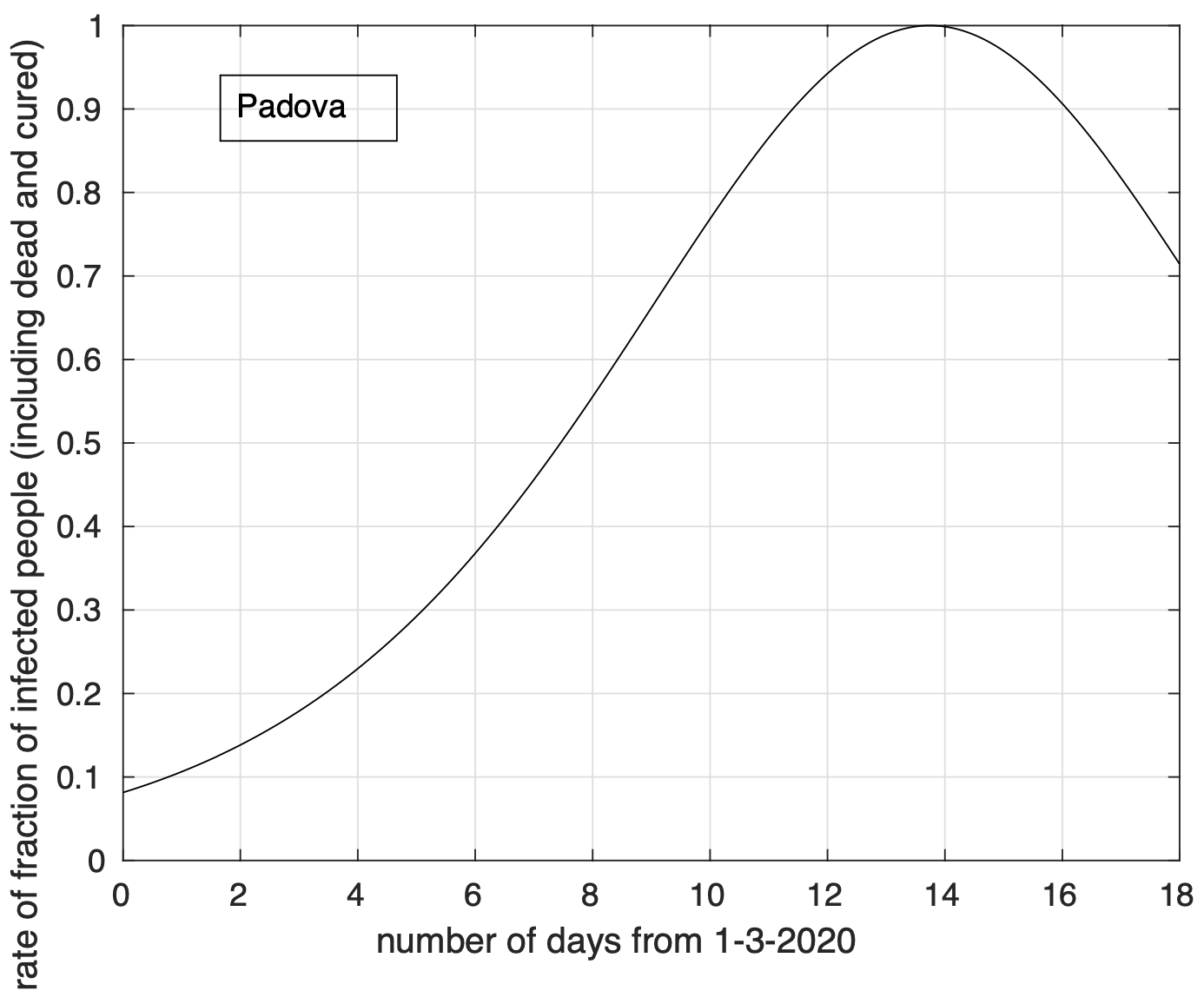
Figura 13. Tasso di crescita della frazione del numero di contagiati osservati a Padova rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il modello teorico adottato è quello logistico.

Figura 14. Tasso di crescita della frazione del numero di contagiati osservati a Piacenza rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il modello teorico adottato è quello doppio logistico.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
Analisi dei dati epidemiologici del coronavirus in Italia (al 18 marzo)
- 7681 letture
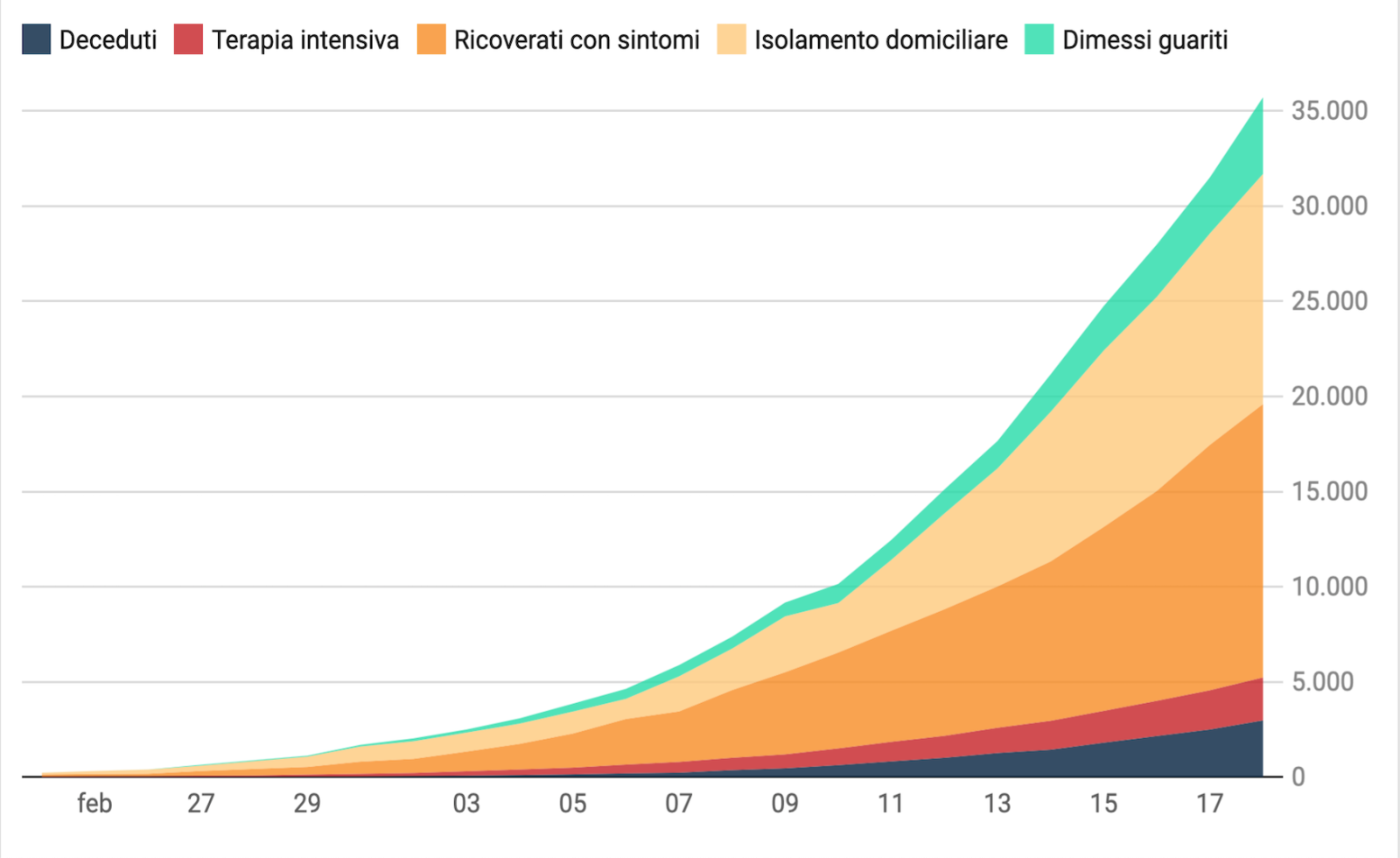
In questo documento sono descritti i risultati relativi all’analisi a livello regionale e per le sei province della Lombardia al momento maggiormente colpite, dei dati aggiornati alle 18 del 18 marzo 2020, che sostituiscono o integrano quelli nel documento del 17 marzo. I dati a livello regionale sono stati scaricati dal sito https://github.com/pcm-dpc/COVID-19 e quelli a livello provinciale dal sito https://github.com/pcm-dpc/COVID-19/tree/master/dati-province.
Per quanto riguarda la Lombardia, si conferma anche per il 18 marzo la piccola ma progressiva riduzione del tasso di crescita della frazione dei contagiati osservati relativa ai giorni precedenti, come si può osservare nella figura 1 ed in modo più evidente nella figura 2 che rappresenta, in funzione del tempo, proprio il tasso di crescita stimato a partire dai dati. Vale l’usuale augurio per i prossimi giorni. Come detto in precedenza, ci aspettiamo che tale riduzione sia progressiva (se non intervengono altri fenomeni collettivi) e che sia dovuta all’introduzione delle misure restrittive sulla mobilità introdotti l’11 marzo. Rimandiamo ai prossimi sette giorni la verifica di questa ipotesi.
Qualitativamente la situazione è la stessa per la maggioranza delle altre regioni, con differenze di tipo quantitativo, come si può vedere nelle figura 3 e 4 per la Campania e la Valle D’Aosta rispettivamente. Poichè il numero di totale di casi in ciascuna regione è ora molto alto, gli errori di misura sono anch’essi grandi e dato che siamo solo all’inizio della fase di diminuzione del tasso di crescita, la stima dei parametri del modello teorico è instabile. Come conseguenza, è possibile che una stessa regione che un giorno presenti una debole riduzione del tasso di crescita, non lo faccia più il giorno successivo, e viceversa. Sulla base dei dati fino al 18 marzo, le regioni che non presentano ancora una diminuzione del tasso di crescita sono il Piemonte, l’Emilia, il Veneto, la Toscana, il Lazio e la Sicilia, come illustrato nelle Figura 7-10. La Basilicata ed il Molise sono state escluse a causa del, per fortuna, basso numero di contagiati osservati fino ad oggi.
Notiamo in tutte le regioni, seppure in modo più o meno marcato, la presenza, nell’intervallo di tempo fino al 10-11 marzo, di un iniziale aumento del tasso di crescita cui segue una sua successiva diminuzione. A partire dall’11-12 marzo il tasso di crescita torna invece di nuovo ad aumentare. Una possibile spiegazione di questo trend, coinvolge sia l’esodo dalla Lombardia avvenuto il 7-8 marzo, non appena si seppe la notizia dell’istituzione della zona rossa in quella regione, che gli assalti ai supermercati dell’8-9 marzo in tutta l’Italia sempre per lo stesso motivo.
Infine, per cinque delle sei le province attualmente maggiormente colpite della Lombardia, Bergamo, Brescia, Cremona, Lodi, Milano, osserviamo una diminuzione del tasso di crescita, con delle differenze tra provincia e provincia come mostrano le figura 11 e 12 per le province di Bergamo e Milano, rispettivamente. Per la provincia di Pavia (vedi figura 13) forse questo accadrà nei prossimi giorni.

Figura 1. Frazione del numero di contagiati osservati in Lombardia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello doppio logistico è sovrapposto ai dati.

Figura 2. Tasso di crescita della frazione del numero di contagiati osservati in Lombardia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. La curva rappresentata è la derivata del modello teorico sovrapposto ai dati in figura 1.
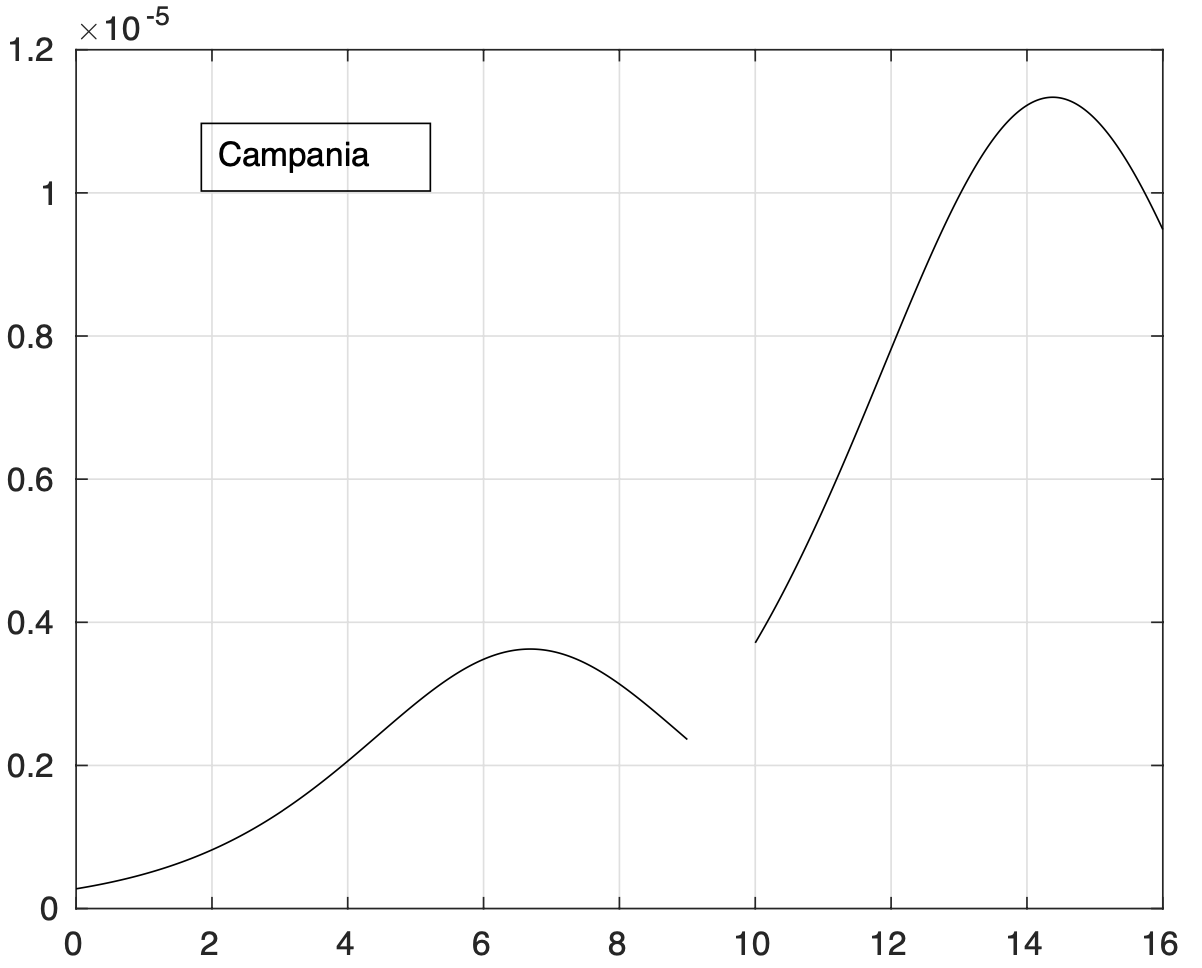
Figura 3. Tasso di crescita della frazione del numero di contagiati osservati in Campania rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo.
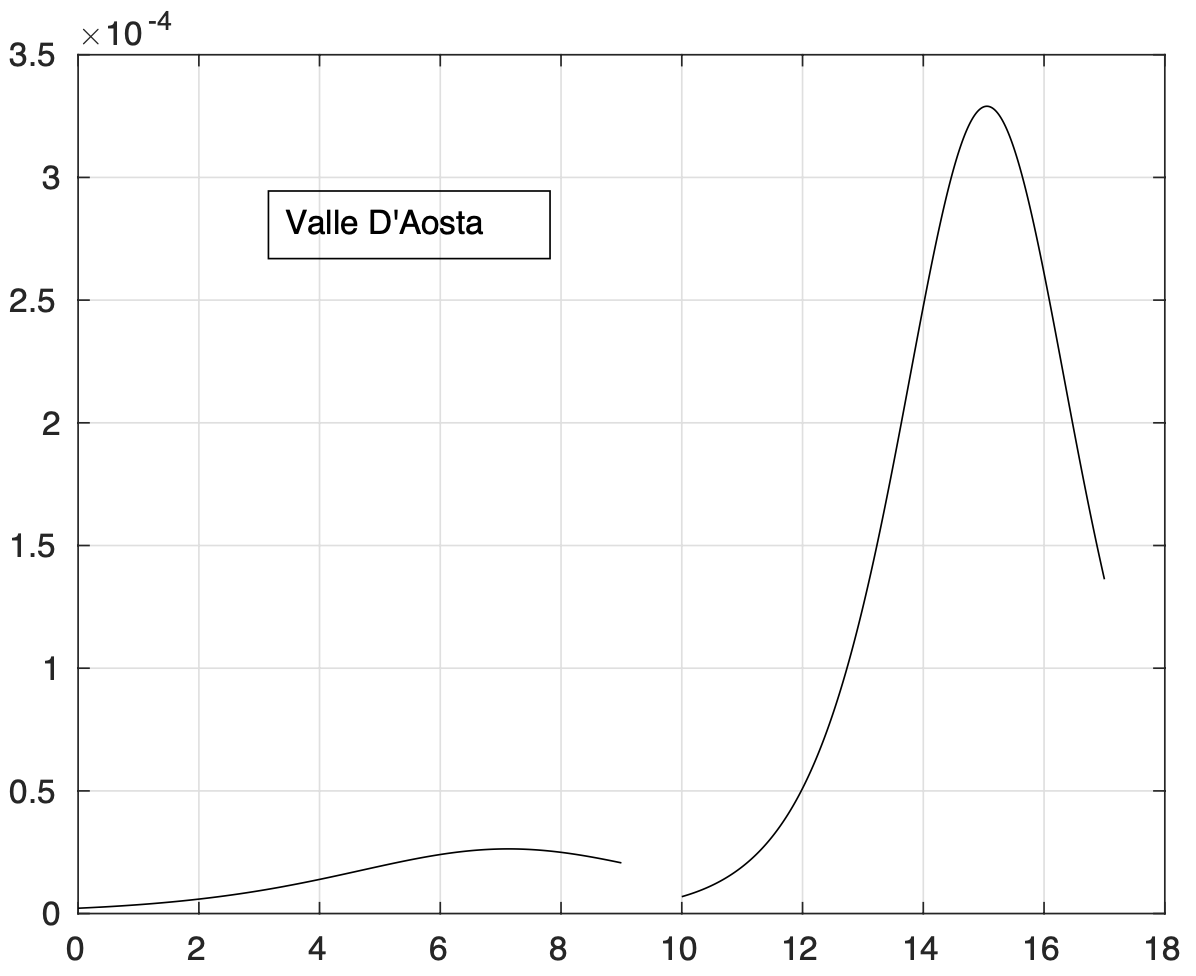
Figura 4. Tasso di crescita della frazione del numero di contagiati osservati nella Valle D’Aosta rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo.
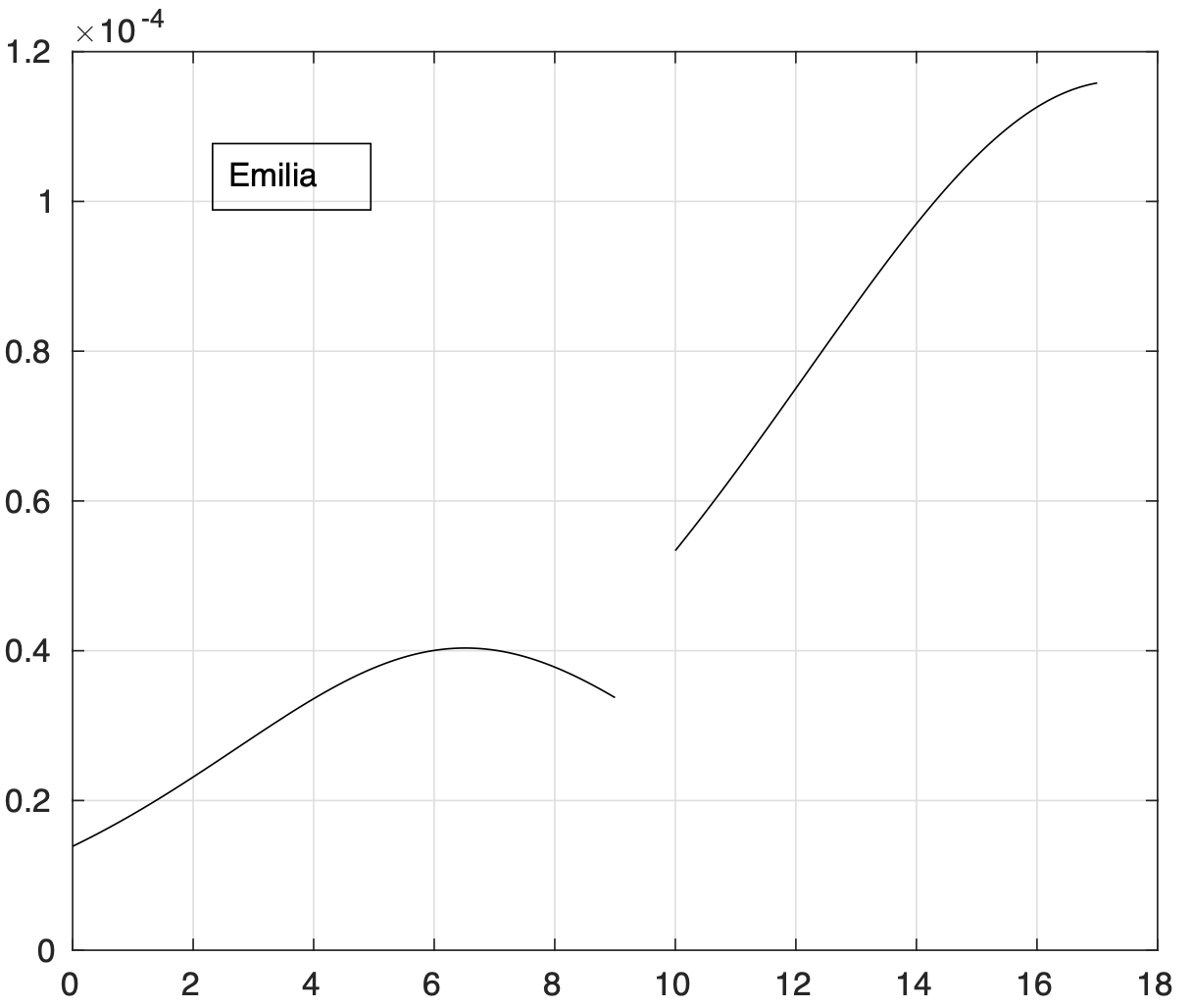
Figura 5. Tasso di crescita della frazione del numero di contagiati osservati in Emilia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo.
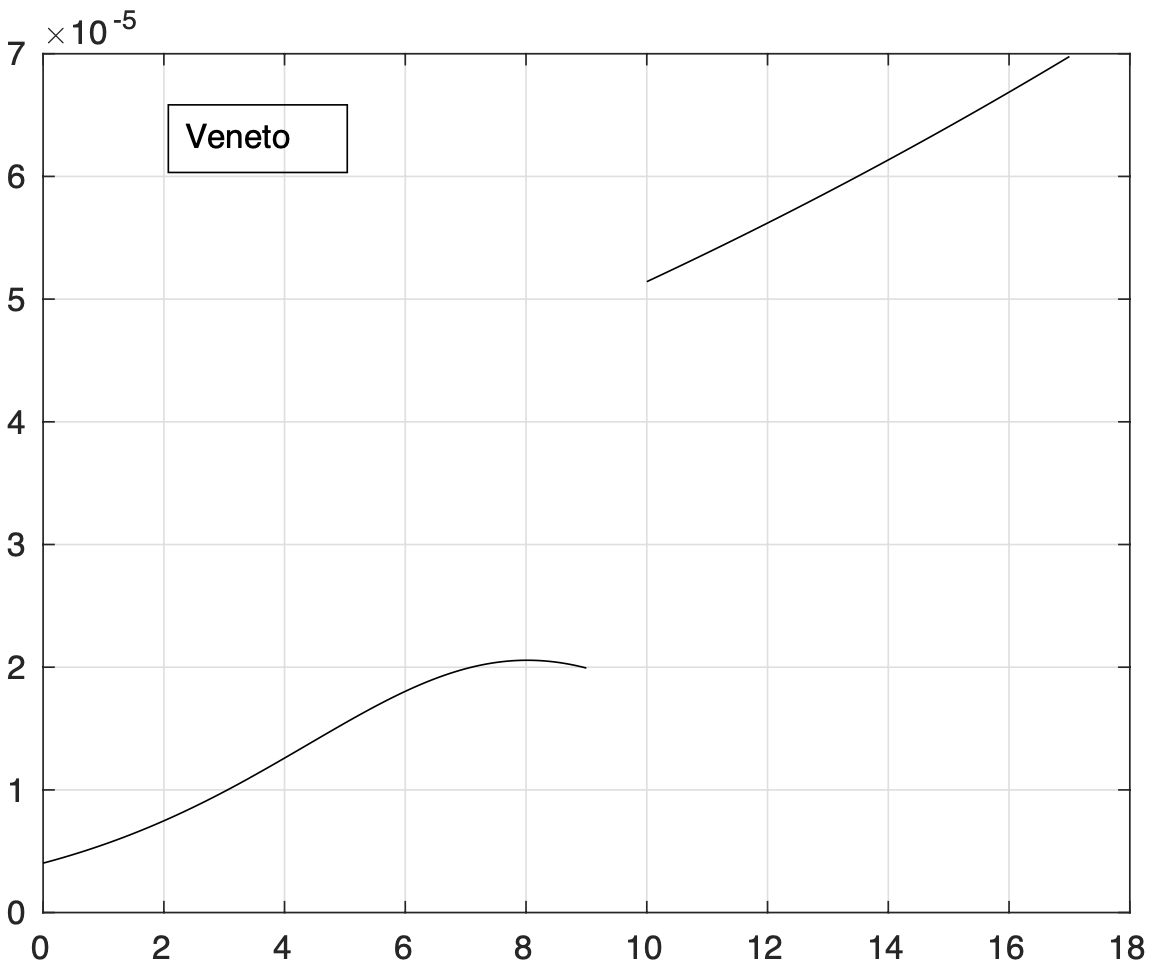
Figura 6. Tasso di crescita della frazione del numero di contagiati osservati in Veneto rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo.

Figura 7. Tasso di crescita della frazione del numero di contagiati osservati in Piemonte rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo.
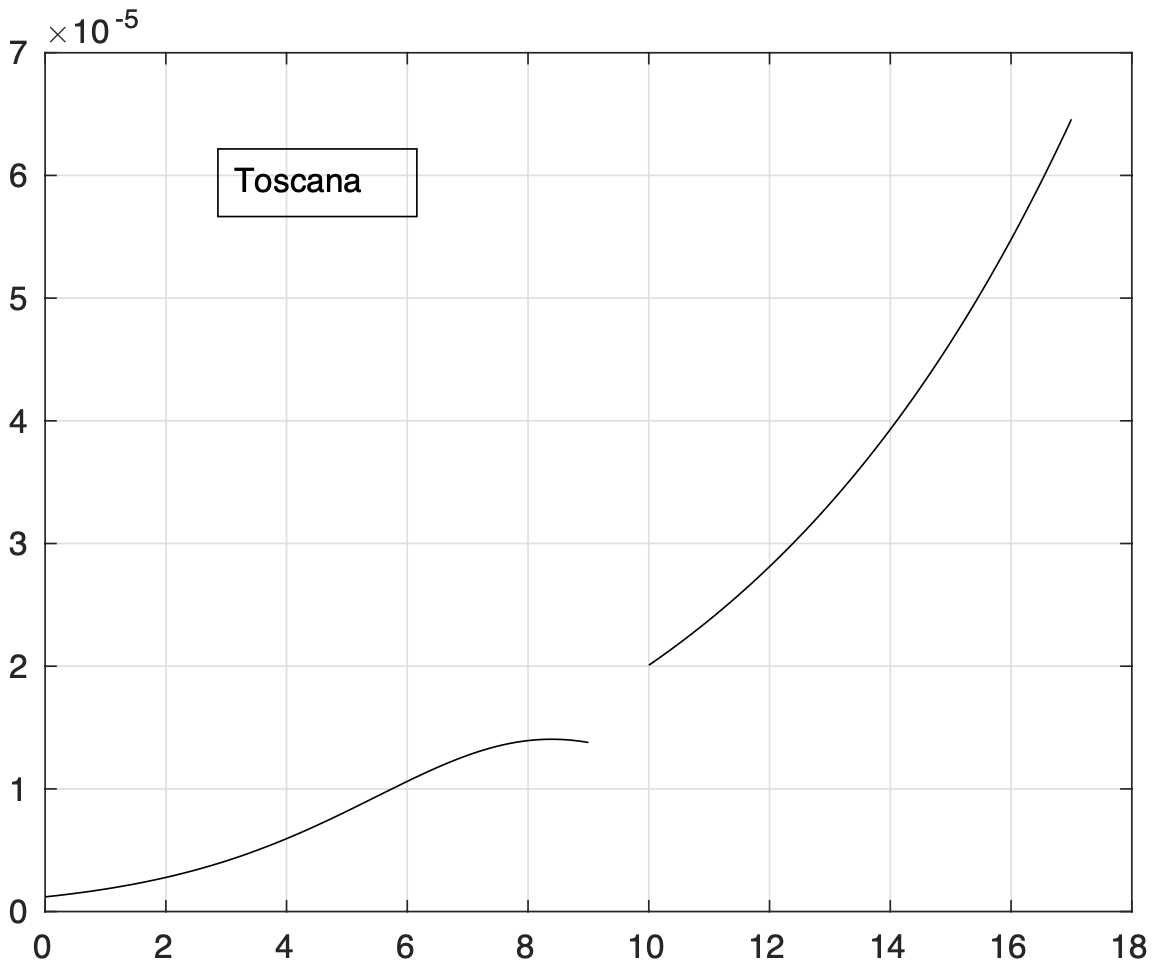
Figura 8. Tasso di crescita della frazione del numero di contagiati osservati in Toscana rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo.
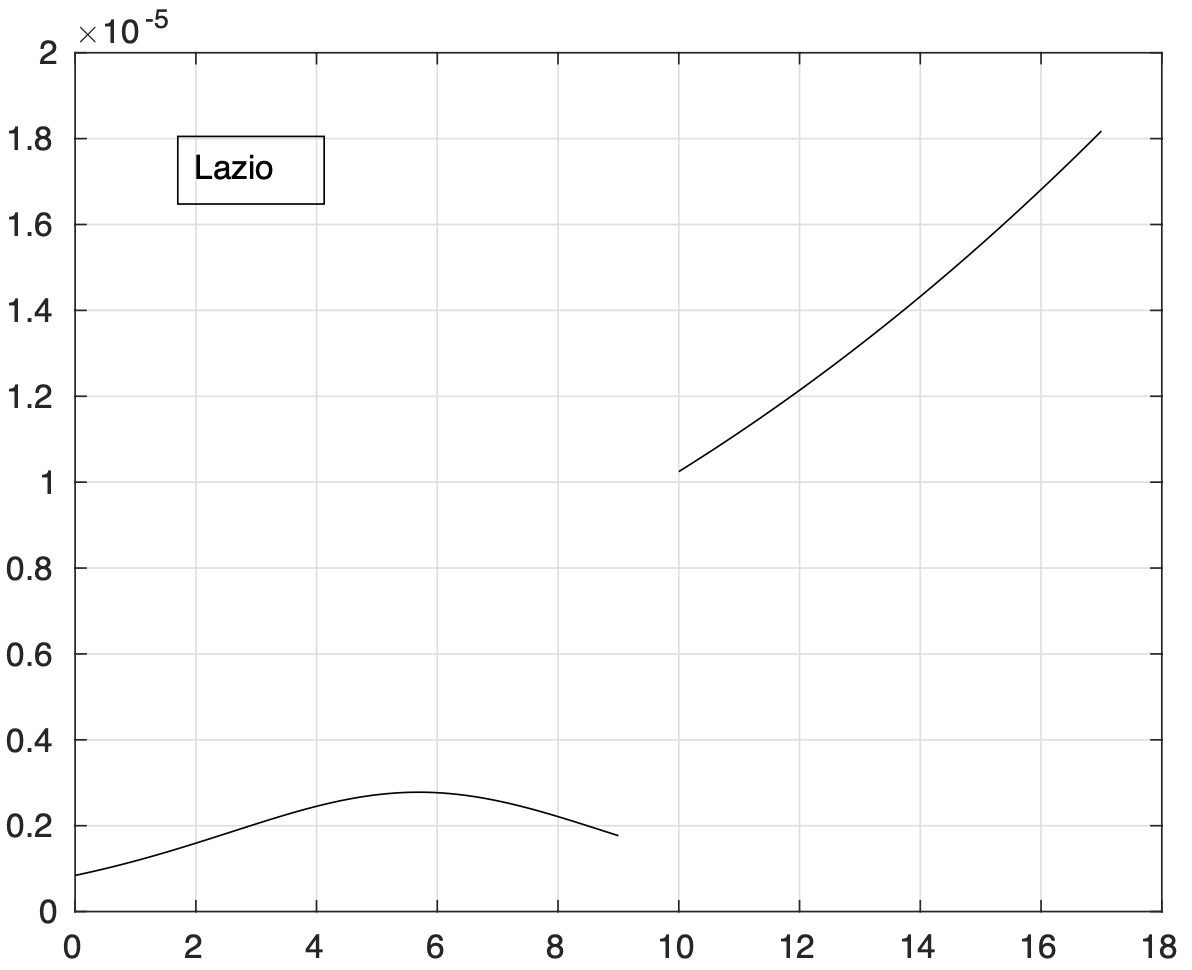
Figura 9. Tasso di crescita della frazione del numero di contagiati osservati nel Lazio rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo.

Figura 10. Tasso di crescita della frazione del numero di contagiati osservati nel Sicilia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo.
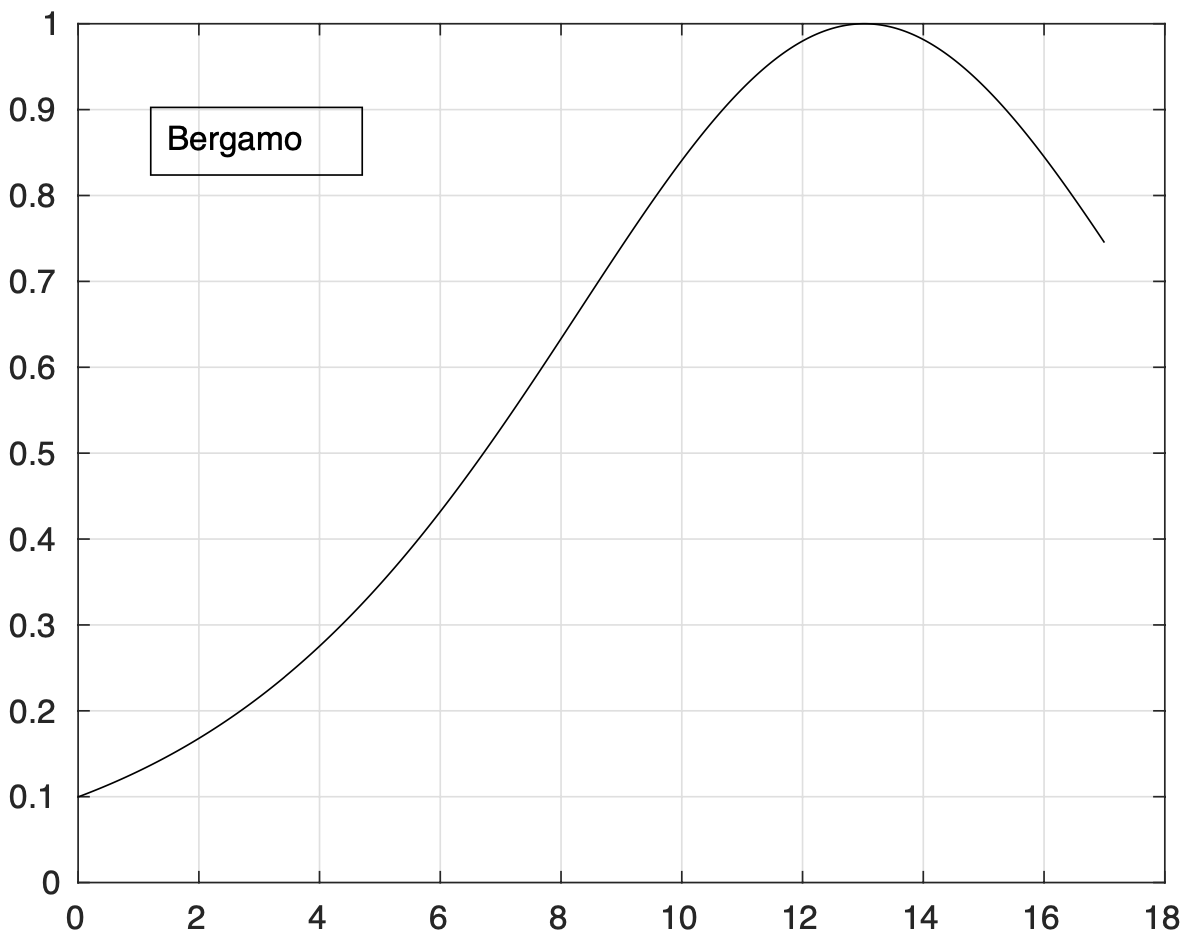
Figura 11. Tasso di crescita della frazione del numero di contagiati osservati nella provincia di Bergamo rispetto alla popolazione della provincia in funzione del tempo a partire dal 1 marzo.
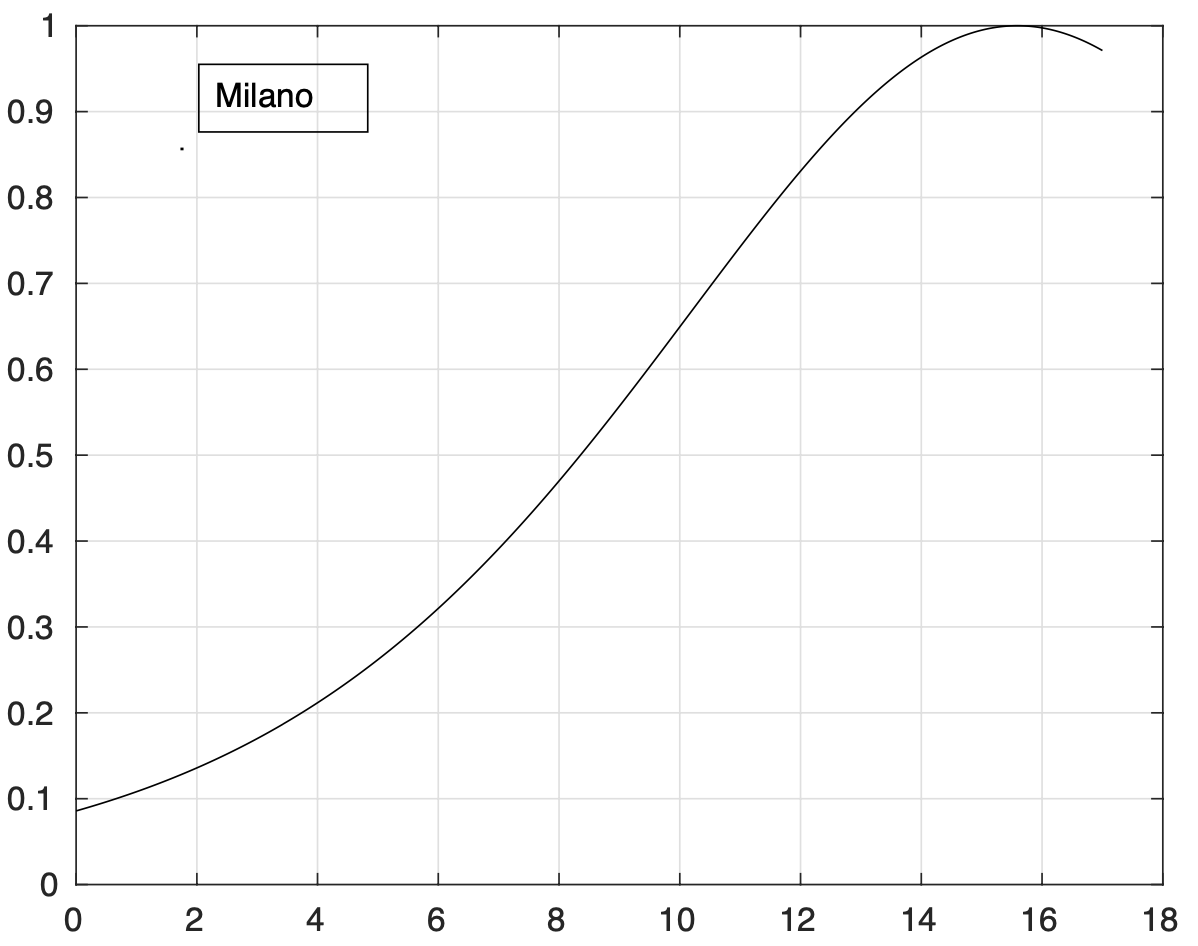
Figura 12. Tasso di crescita della frazione del numero di contagiati osservati nella provincia di Milano rispetto alla popolazione della provincia in funzione del tempo a partire dal 1 marzo.
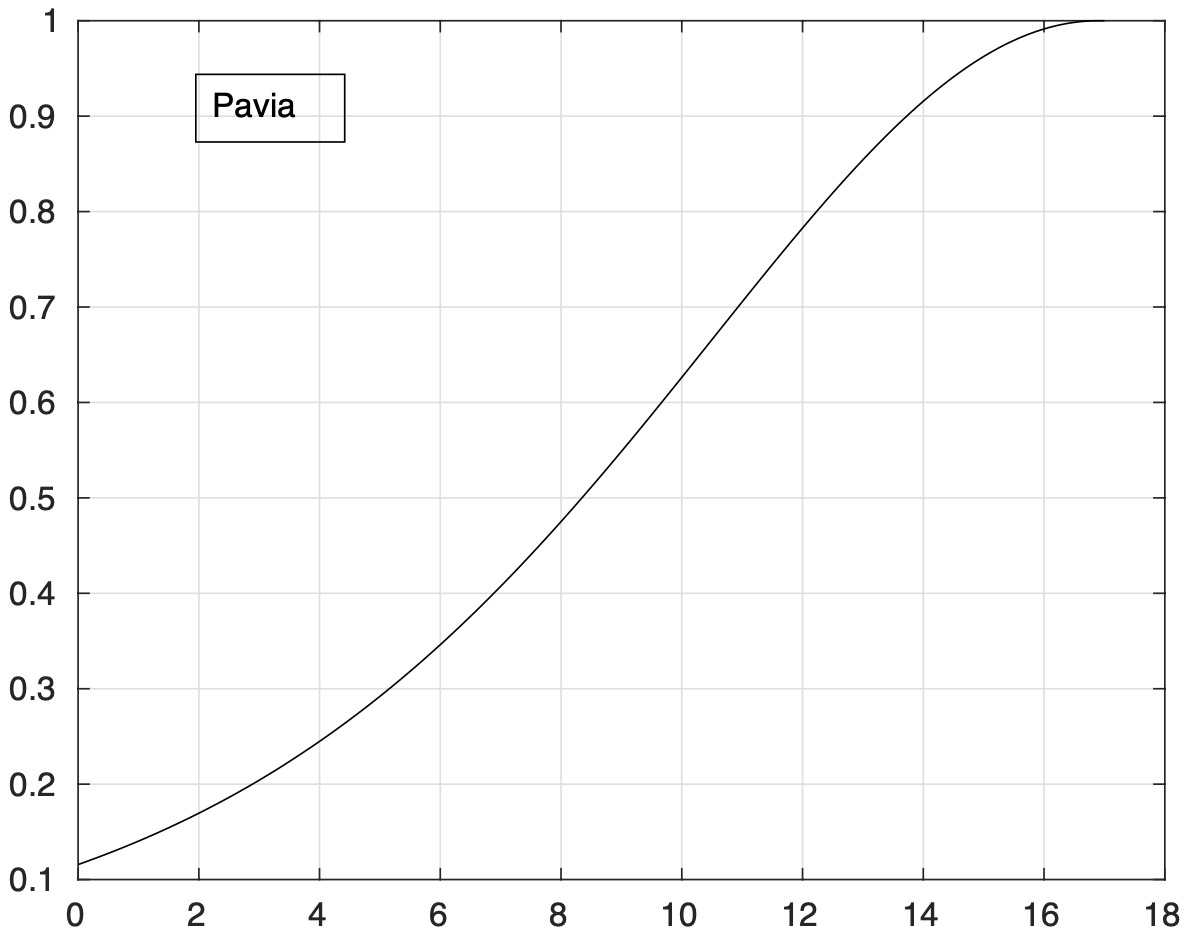
Figura 13. Tasso di crescita della frazione del numero di contagiati osservati nella provincia di Pavia rispetto alla popolazione della provincia in funzione del tempo a partire dal 1 marzo.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
Analisi dei dati epidemiologici del coronavirus in Italia (al 17 marzo)
- 9485 letture
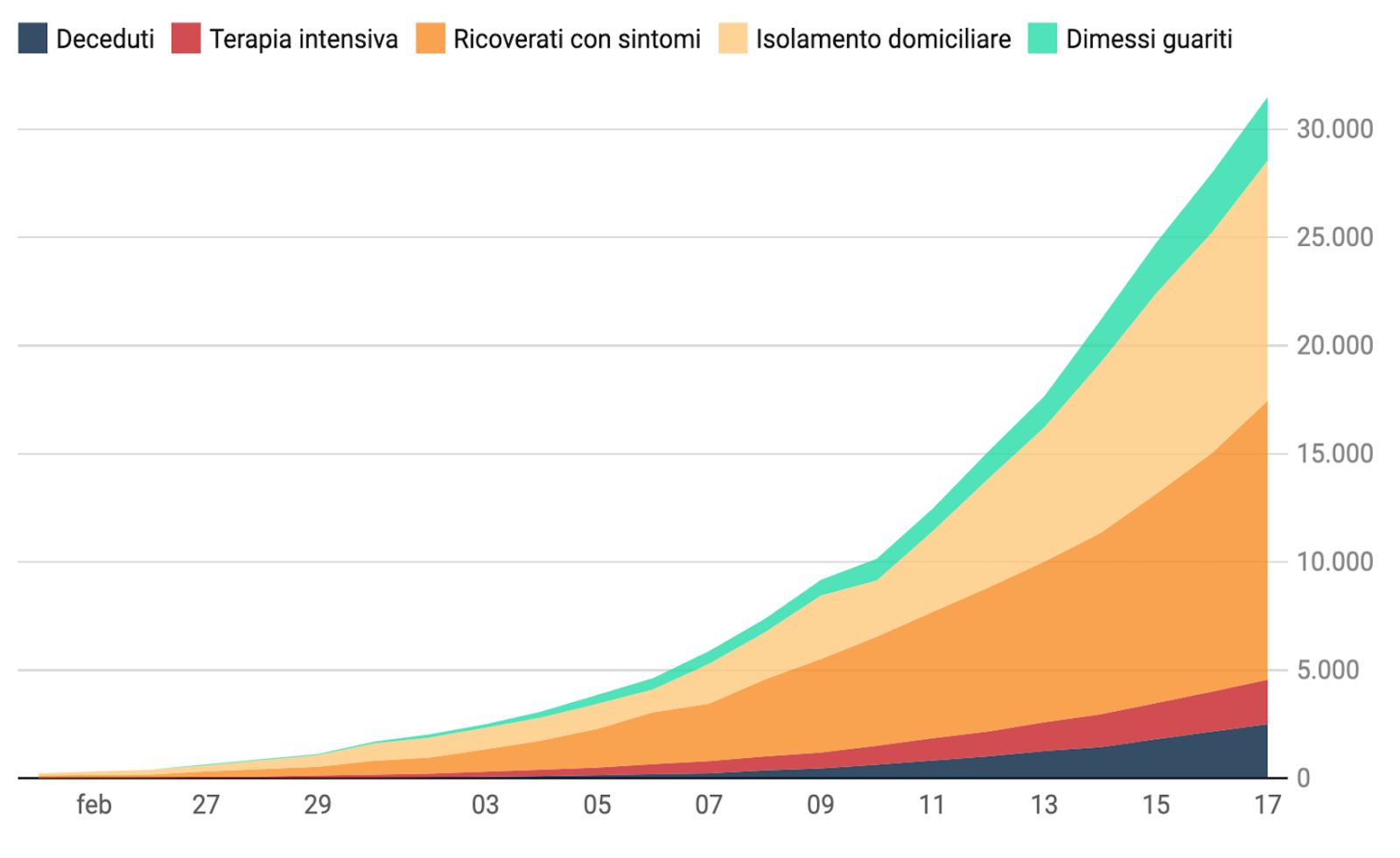
In questo documento sono descritti i risultati relativi all’analisi a livello regionale e per le sei province della Lombardia al momento maggiormente colpite, dei dati aggiornati alle 18 del 17 marzo 2020, che sostituiscono o integrano quelli nel documento del 16 Marzo. I dati a livello regionale sono stati scaricati dal sito https://github.com/pcm-dpc/COVID-19 e quelli a livello provinciale dal sito https://github.com/pcm-dpc/COVID-19/tree/master/dati-province.
Per quanto riguarda la Lombardia, si conferma anche per il 16-17 marzo la piccola ma progressiva riduzione del tasso di crescita della frazione dei contagiati osservati relativa ai giorni precedenti, come si può osservare nella figura 1 ed in scala semi-logaritmica nella figura 2. Vale l’usuale augurio per i prossimi giorni. Come detto in precedenza, ci aspettiamo che tale riduzione sia progressiva (se non intervengono altri fenomeni collettivi) e che sia dovuta all’introduzione delle misure restrittive sulla mobilità introdotti l’11 marzo. Rimandiamo ai prossimi giorni la verifica di questa ipotesi. Qualitativamente la situazione è la stessa per la maggioranza delle altre regioni, con differenze di tipo quantitativo. Simile alla Lombardia è per esempio il caso dell’Emilia (vedi figura 3), mentre l’evidenza aumenta passando alla Toscana, poi alle Marche e quindi al Friuli, come si può vedere nelle figure 4, 5 e 6.
Invece, per il Piemonte, l’Abruzzo e la Calabria si osserva ancora un aumento del tasso di crescita nella parte finale della curva, come mostrato nelle figure 7, 8, 9, mentre per la Sicilia il tasso di crescita nell’ultima parte della curva sembra costante (vedi figura 10). La Basilicata ed il Molise sono state escluse a causa del basso numero di contagiati osservati fino a oggi. Per la restante regione del sud, la Puglia non possiamo dire niente a causa di un errore nei dati ufficiali relativi al giorno 16 Marzo (vedi Figura 11).
Una caratteristica presente in tutte le regioni a esclusione della Lombardia, seppure in modo più o meno marcato, è l’aumento del tasso di crescita avvenuto attorno all’11-12 Marzo dopo una sua precedente diminuzione. Questo può essere apprezzato nelle figure precedenti e per il caso della Sardegna in figura 12. In quest’ultimo caso e per l’Abruzzo (vedi figura 8), abbiamo anche evidenza di una discontinuità della curva della frazione dei contagiati osservati. Una possibile spiegazione di questo trend, che sottolineiamo è presente in tutte le regioni meno la Lombardia, coinvolge l’esodo proprio dalla Lombardia avvenuto l’8 marzo, giorno in cui venne istituita la zona rossa in quella regione.
Infine, per la prima volta accade che per tutte e sei le province attualmente maggiormente colpite della Lombardia, Bergamo, Brescia, Cremona, Lodi, Milano e Pavia osserviamo una diminuzione del tasso di crescita. Infatti anche Pavia mostra una lieve riduzione del tasso relativa ai giorni 15-16 e 16-17 marzo (vedi figura 13). Questa andrà confermato nei prossimi giorni.
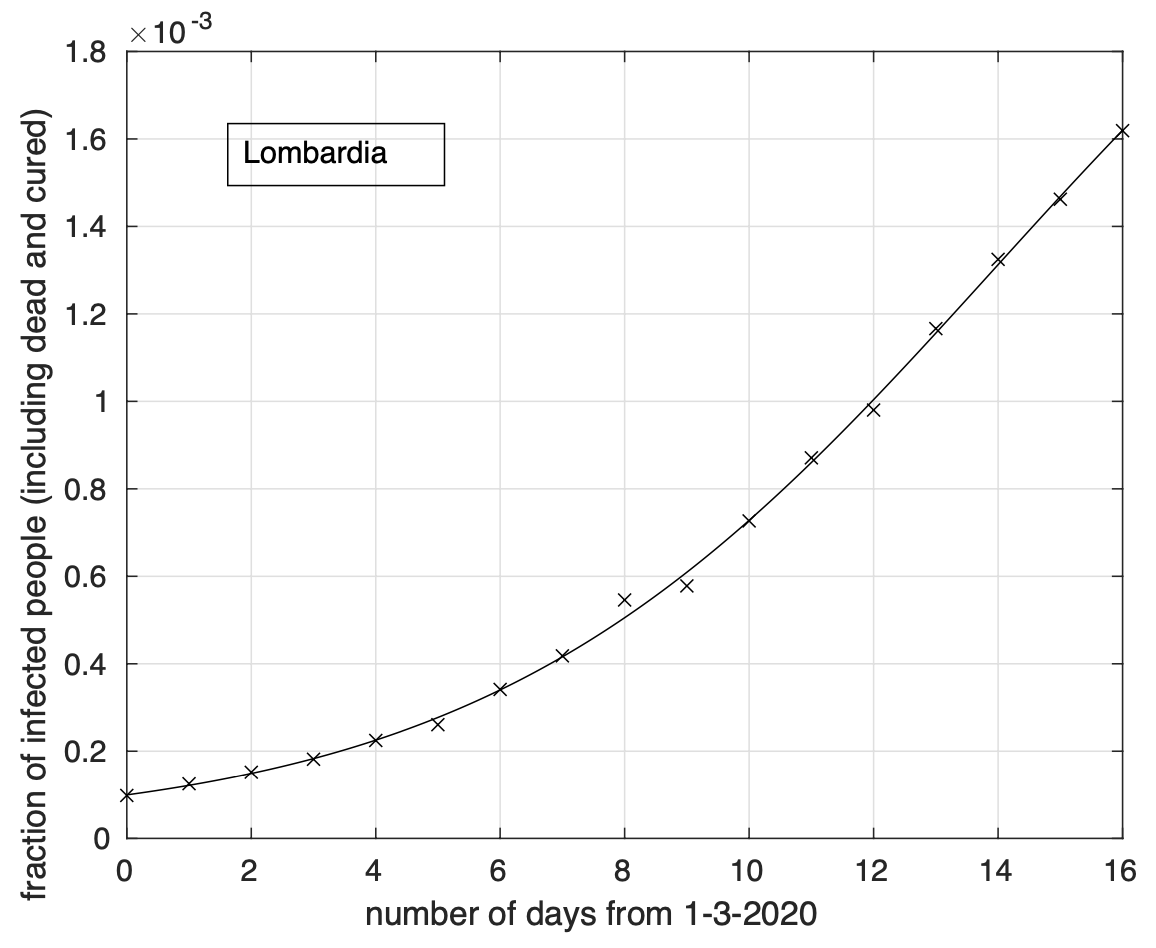
Figura 1. Frazione del numero di contagiati osservati in Lombardia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati.
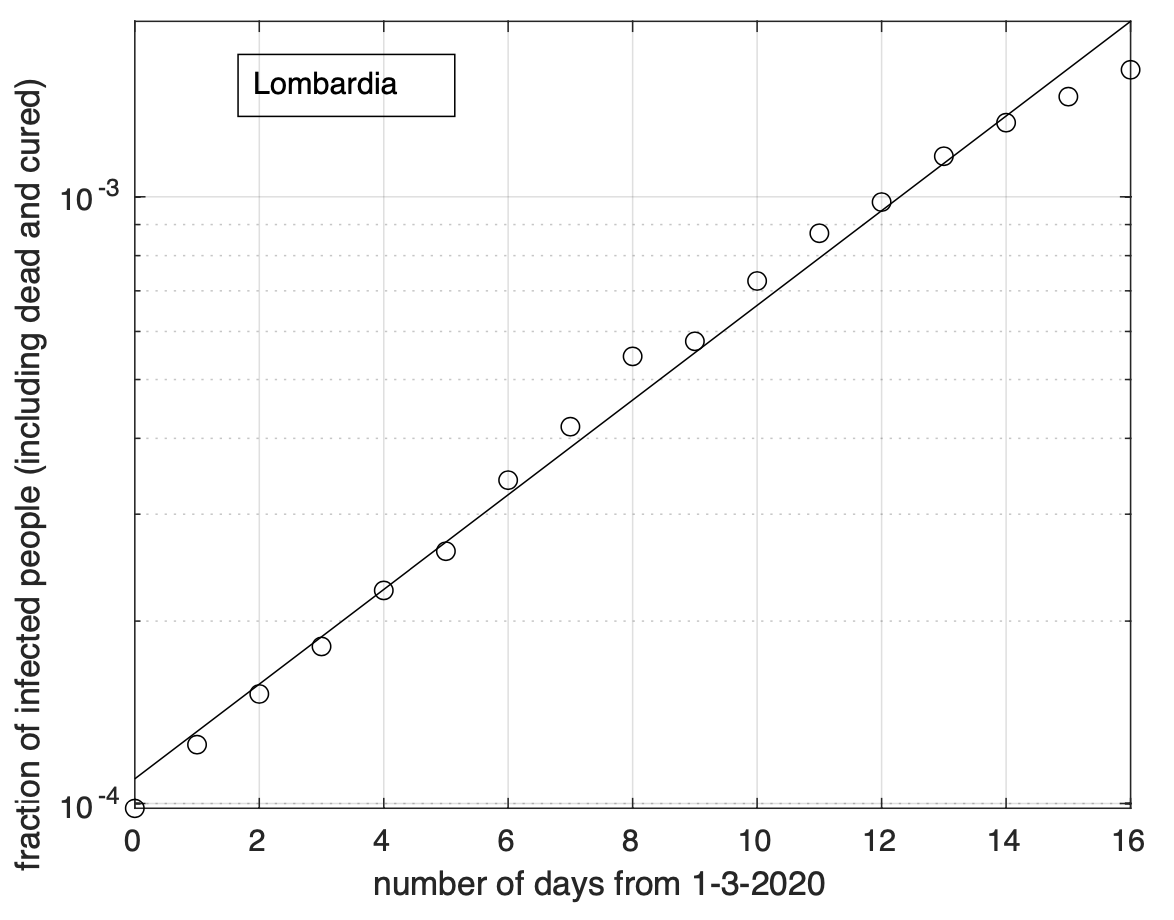
Figura 2. Frazione del numero di contagiati osservati in Lombardia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo e in scala semi-logaritmica. La linea retta rappresenta il modello geometrico stimato a partire dai dati. Notiamo che gli ultimi punti sperimentali sono sotto la retta che corrisponde al miglior fit con un modello geometrico. Questo fornisce evidenza del trend di riduzione del tasso di crescita.
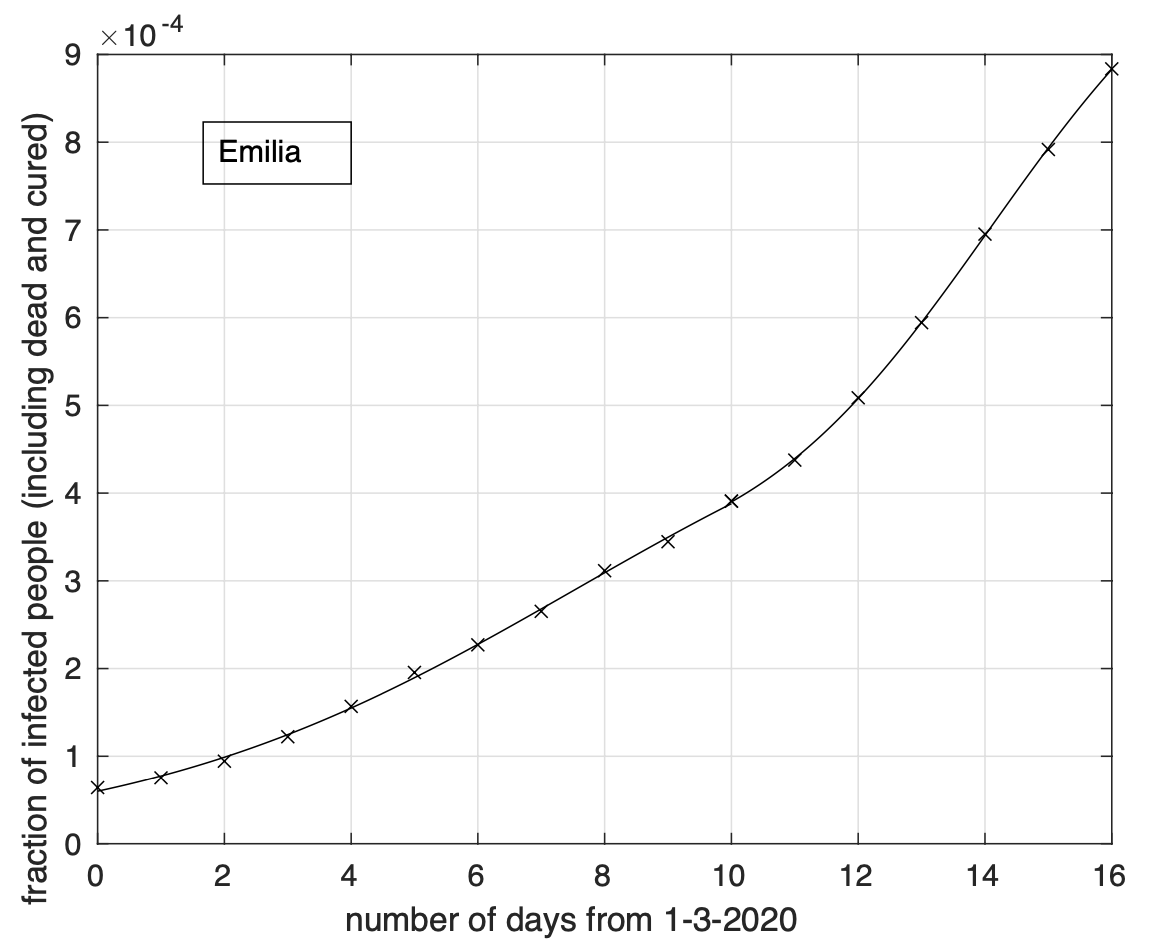
Figura 3. Frazione del numero di contagiati osservati in Emilia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati.
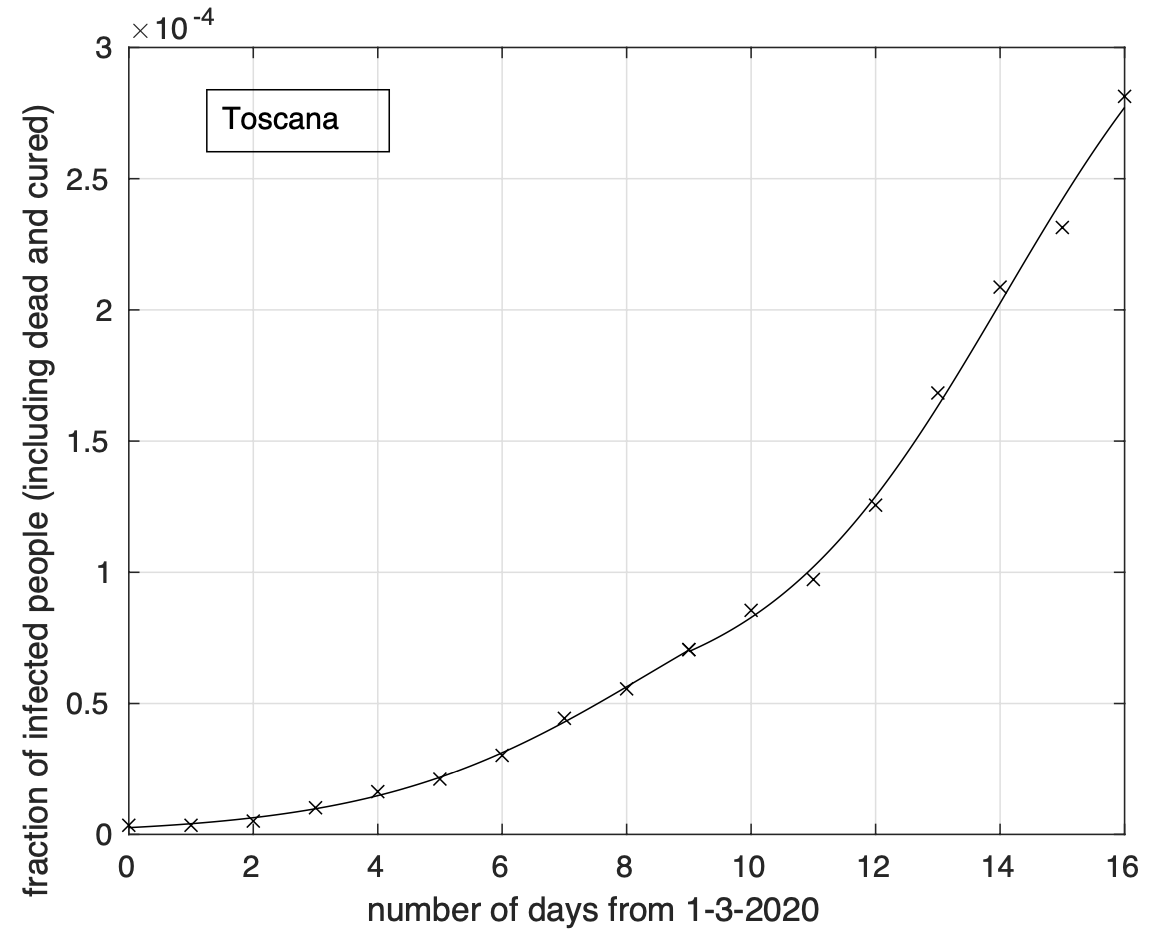
Figure 4. Frazione del numero di contagiati osservati in Toscana rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati.
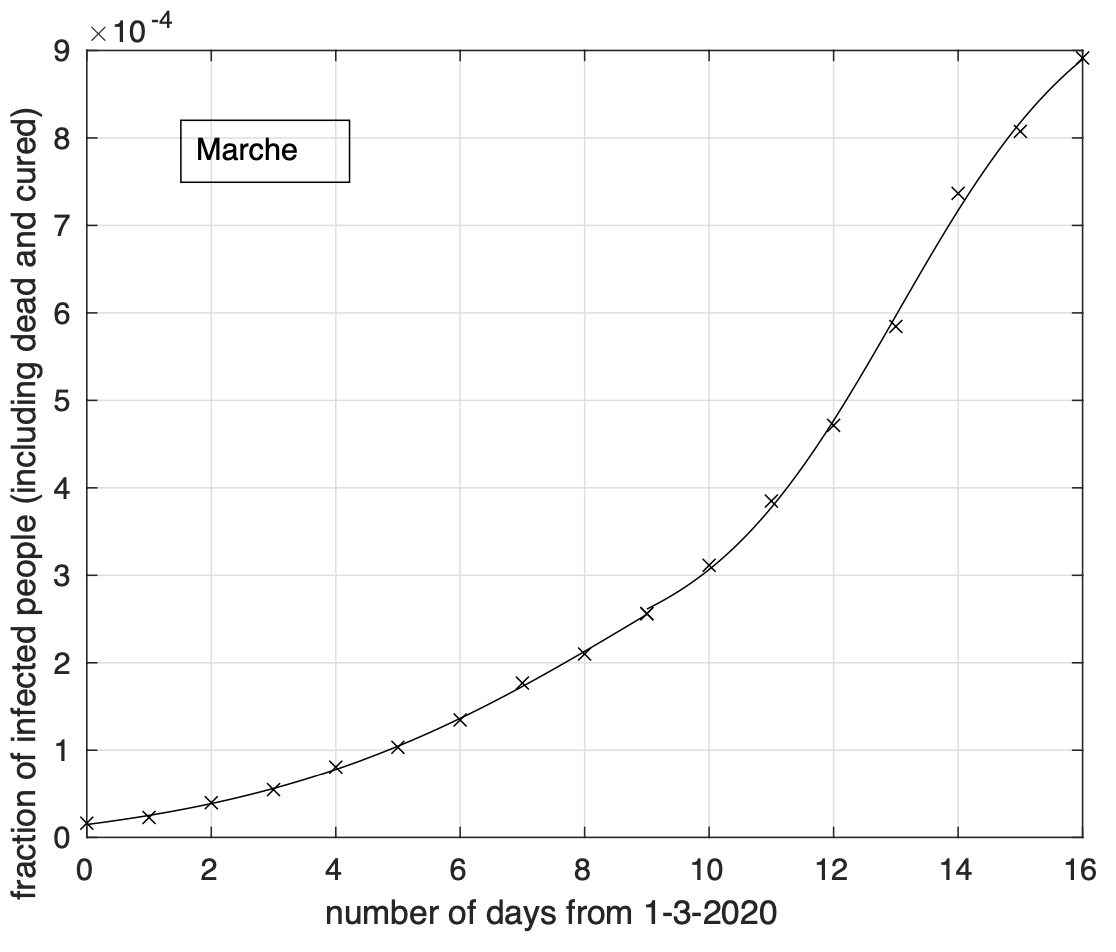
Figure 5. Frazione del numero di contagiati osservati nelle Marche rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati.

Figura 6. Frazione del numero di contagiati osservati nel Friuli rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati.
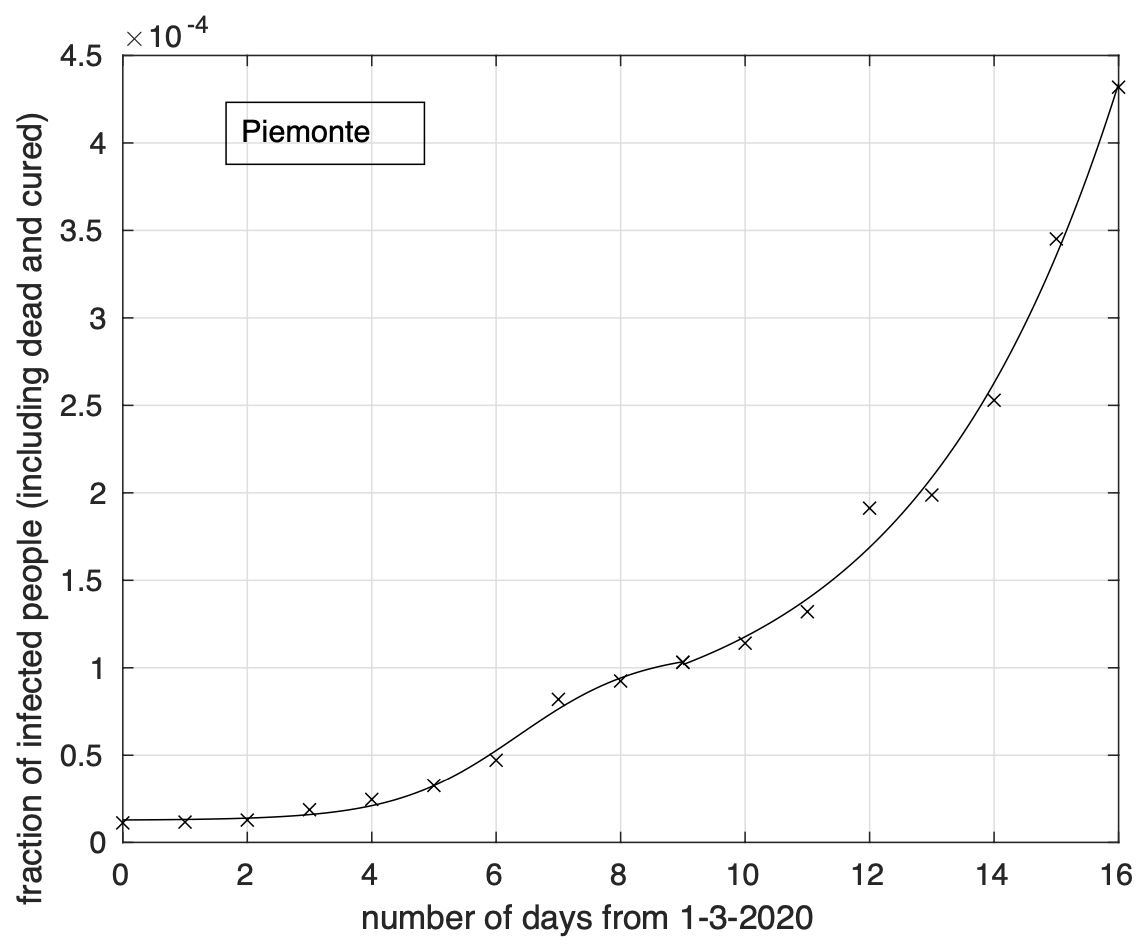
Figura 7. Frazione del numero di contagiati osservati nel Piemonte rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati.

Figura 8. Frazione del numero di contagiati osservati nell’Abruzzo rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati.
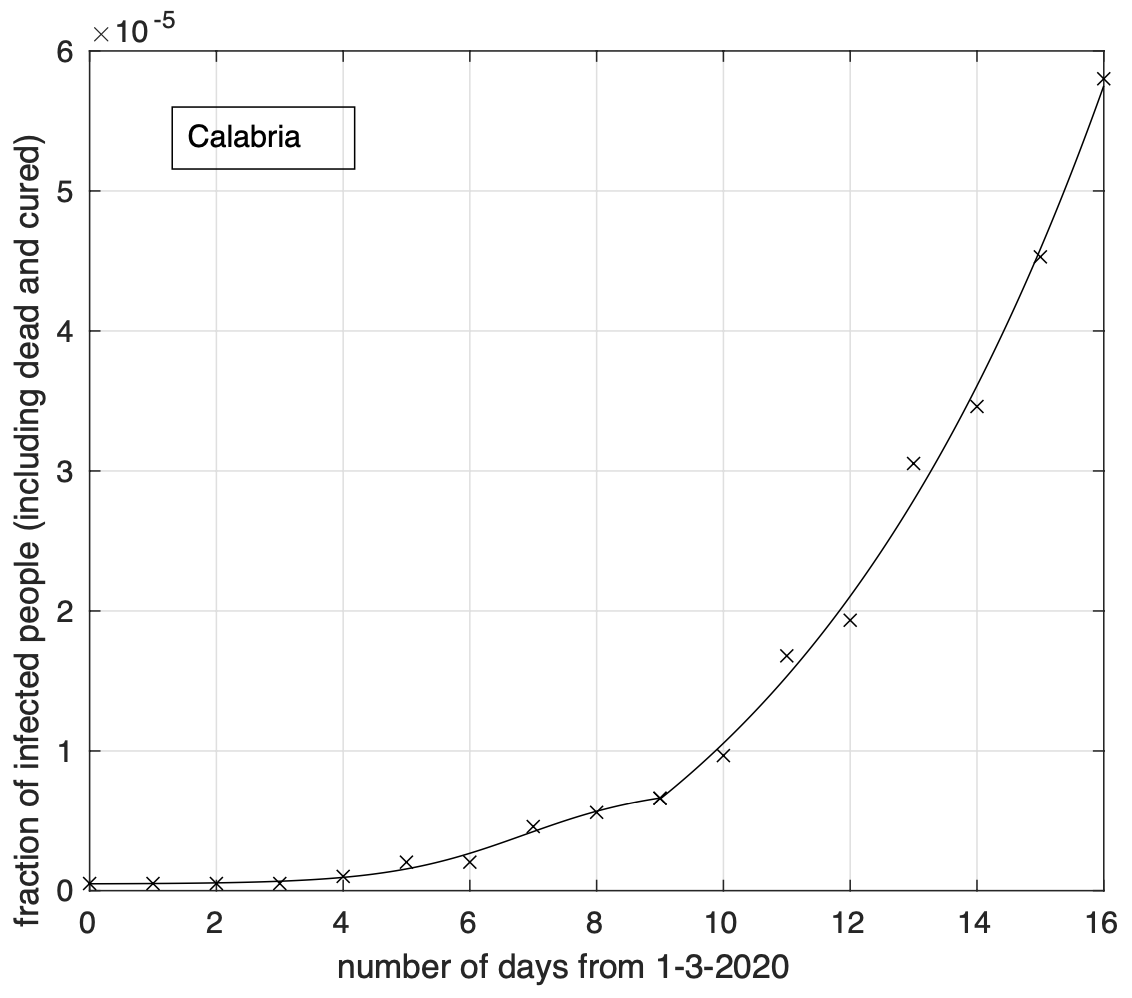
Figura 9. Frazione del numero di contagiati osservati in Calabria rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati.

Figura 10. Frazione del numero di contagiati osservati in Sicilia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati.
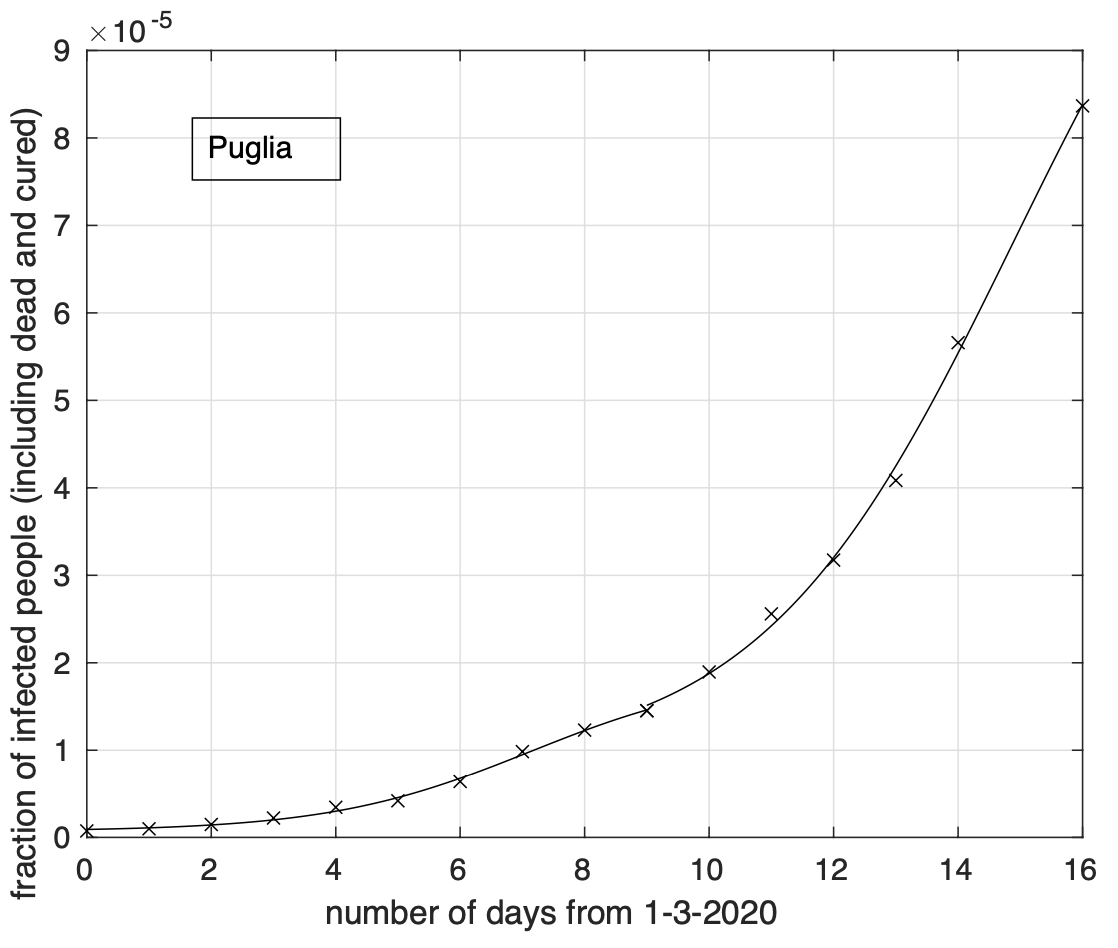
Figure 11. Frazione del numero di contagiati osservati in Puglia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati.
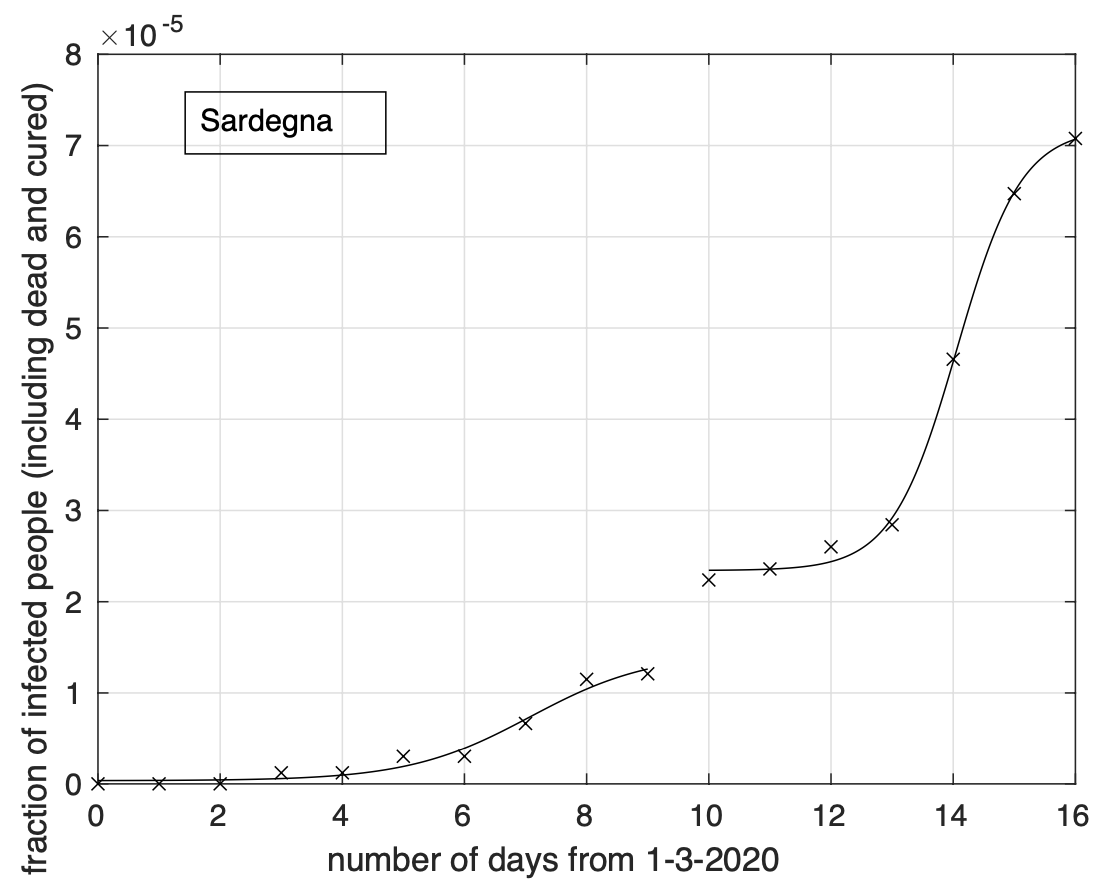
Figura 12. Frazione del numero di contagiati osservati in Sardegna rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati.

Figura 13. Sequenza temporale della frazione dei contagiati osservati nella provincia di Pavia rispetto alla popolazione della provincia (in scala semi-logaritmica). Il miglior fit con un modello geometrico è sovrapposto ai dati.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
Analisi dei dati epidemiologici del coronavirus in Italia (al 16 marzo)
- 11727 letture
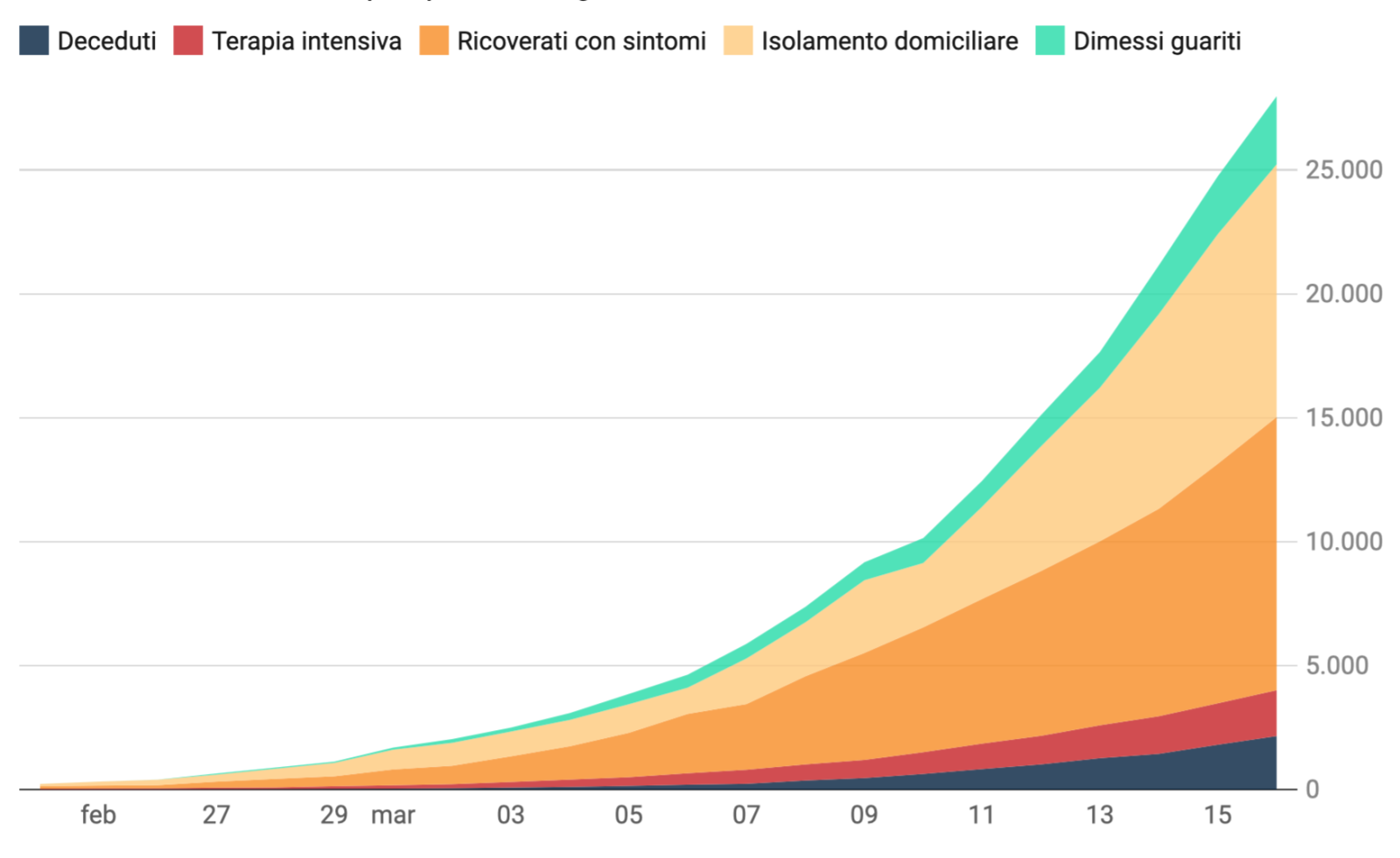
In questo documento sono descritti i risultati relativi all’analisi per la Lombardia, le regioni del centro, quelle del sud e per le sei province della Lombardia al momento maggiormente colpite, dei dati aggiornati alle 18 del 16 marzo 2020, che sostituiscono o integrano quelli nel documento del 15 marzo. I dati a livello regionale sono stati scaricati dal sito https://github.com/pcm-dpc/COVID-19 e quelli a livello provinciale dal sito https://github.com/pcm-dpc/COVID-19/tree/master/dati-province.
Per quanto riguarda la Lombardia, si conferma anche per il 15-16 marzo in modo più evidente la seppur piccola riduzione del tasso di crescita della frazione dei contagiati osservati relativa ai giorni 12-13 marzo, 13-14 marzo e 14-15 marzo, come si può osservare nella figura 1 ed in scala semi-logaritmica nella figura 2. Ci auguriamo la permenenza del trend anche nei prossimi giorni. Osserviamo che oggi 16 marzo siamo a cinque giorni dall’introduzione del decreto “Io resto a casa” e che il valor medio del tempo tra il contagio e l’insorgenza dei sintomi è cinque giorni. Come però riportato in un rapporto dell’Istituto Superiore di Sanità, il valor medio del tempo tra l’insorgenza dei sintomi e la diagnosi è 2-4 giorni, per cui se, come crediamo, l’introduzione delle misure restrittive sulla mobilità sono efficaci per la riduzione del rischio di contagio, ci aspettiamo di osservare una significativa riduzione del tasso di crescita tra circa tre giorni. Evidenza della riduzione del tasso di crescita si nota anche nella figura 3 nel blocco di regioni non confinanti con la Lombardia del centro Italia: Toscana, Umbria, Marche, Lazio ed Abruzzo. Anche qui valgono le considerazioni precedenti sul valor medio del tempo tra infezione e diagnosi. Nella figura 4 è rappresentata la situazione per le tre regioni del sud Italia: Campania, Calabria e Sicilia. La Basilicata e il Molise sono state escluse a causa del, per fortuna, basso numero di contagiati osservati fino a oggi, mentre per la Puglia, come dichiarato in conferenza stampa dalla Protezione civile, mancano alcuni dati e i valori del 16 marzo e del 15 marzo dei contagiati osservati sono uguali. Da questa figura, come già sottolineato in precedenza, osserviamo l’aumento del tasso di crescita attorno all’11-12 marzo successivo a una precedente sua riduzione, probabilmente causato dall’esodo di tre-quattro giorni prima, l’8 marzo, quando si è diffusa la notizia del decreto, uscito in Gazzetta alle 13, che istituiva la zona rossa in Lombardia. Gli effetti del decreto “Io resto a casa”, introdotto cinque giorni fa, al momento non sono evidenti dal grafico probabilmente perché sono stati compensati dall’impulso alla diffusione dell’epidemia dato dall’esodo di persone contagiate.
Come nei giorni precedenti, per cinque delle sei province attualmente maggiormente colpite della Lombardia, Bergamo, Brescia, Cremona, Lodi, Milano e Pavia osserviamo una diminuzione del tasso di crescita, a parte Pavia. Infatti per Pavia l’adattamento del modello geometrico (che non presenta riduzione del tasso di crescita) ai dati è molto buono (vedi figura 5).
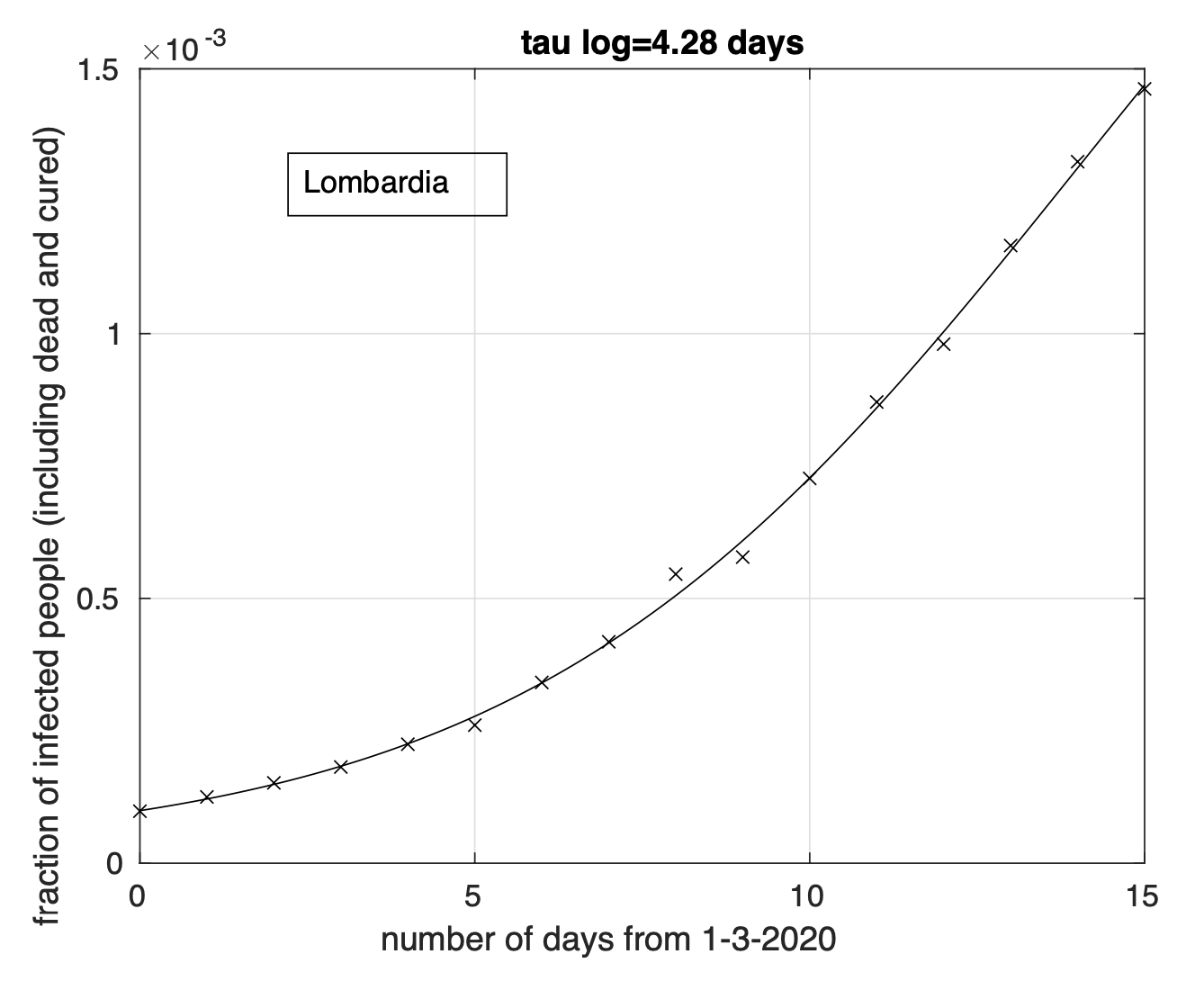
Figura 1. Frazione del numero di contagiati osservati in Lombardia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello logistico è sovrapposto ai dati.
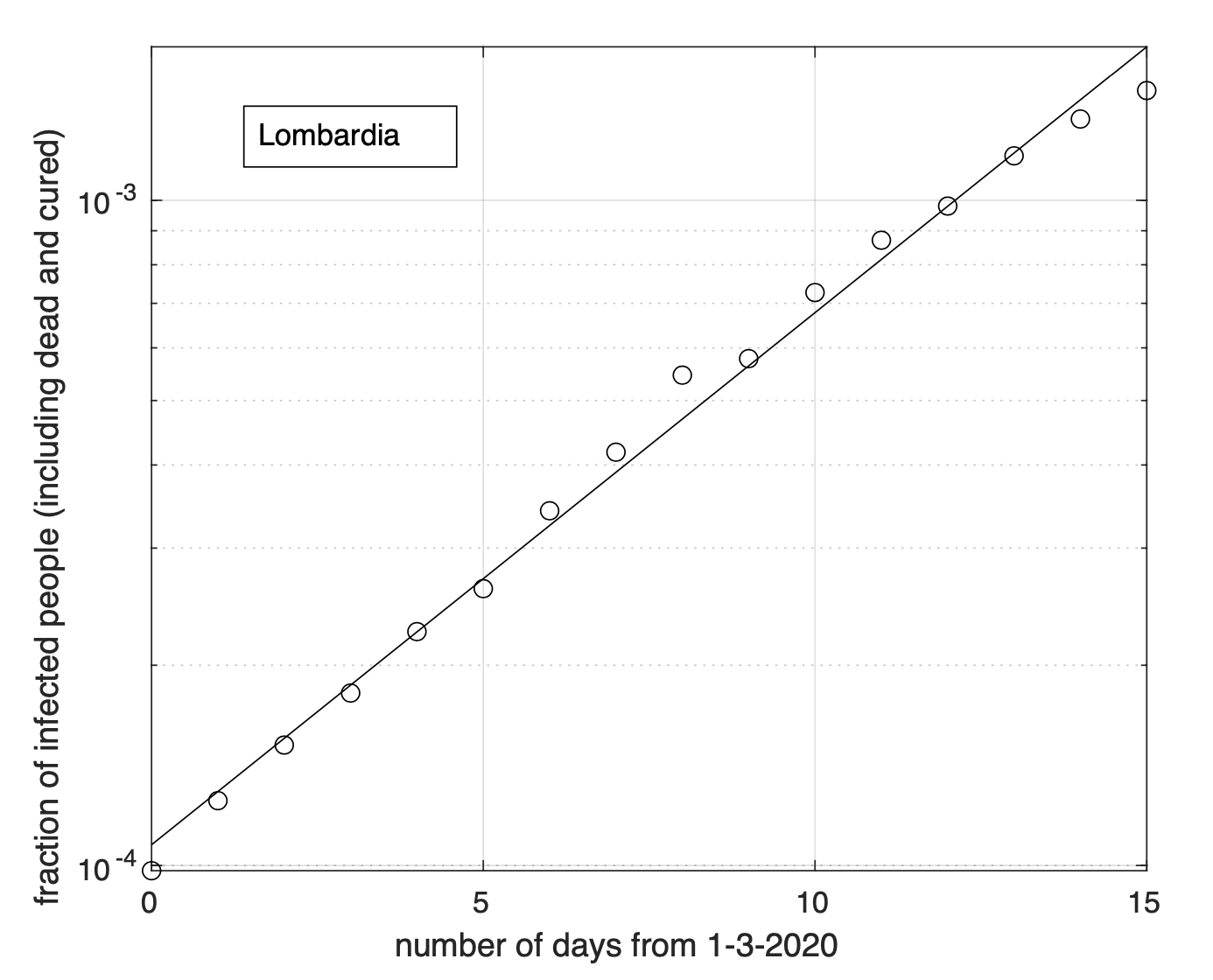
Figura 2. Frazione del numero di contagiati osservati in Lombardia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo ed in scala semi-logaritmica. La linea retta rappresenta il modello geometrico stimato a partire dai dati. Notiamo un buon adattamento del modello teorico ai dati e che gli ultimi tre punti sperimentali sono sotto la retta che corrisponde al miglior fit con un modello geometrico. Questo fornisce evidenza del trend di riduzione del tasso di crescita.
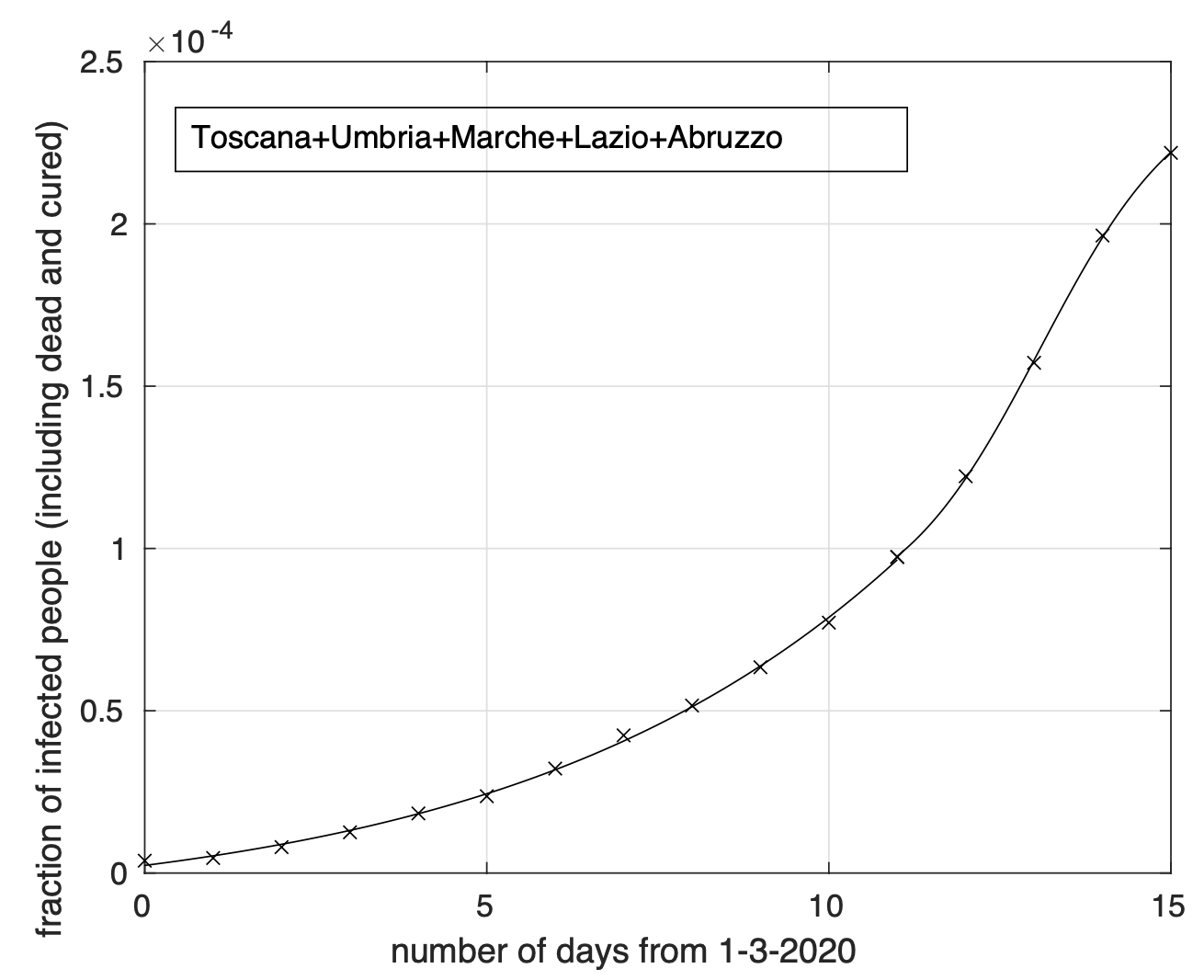
Figura 3. Frazione del numero di contagiati osservati nelle regioni del centro Italia: Toscana, Umbria, Marche, Lazio ed Abruzzo rispetto alla somma delle rispettive popolazioni in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello doppio logistico è sovrapposto ai dati.
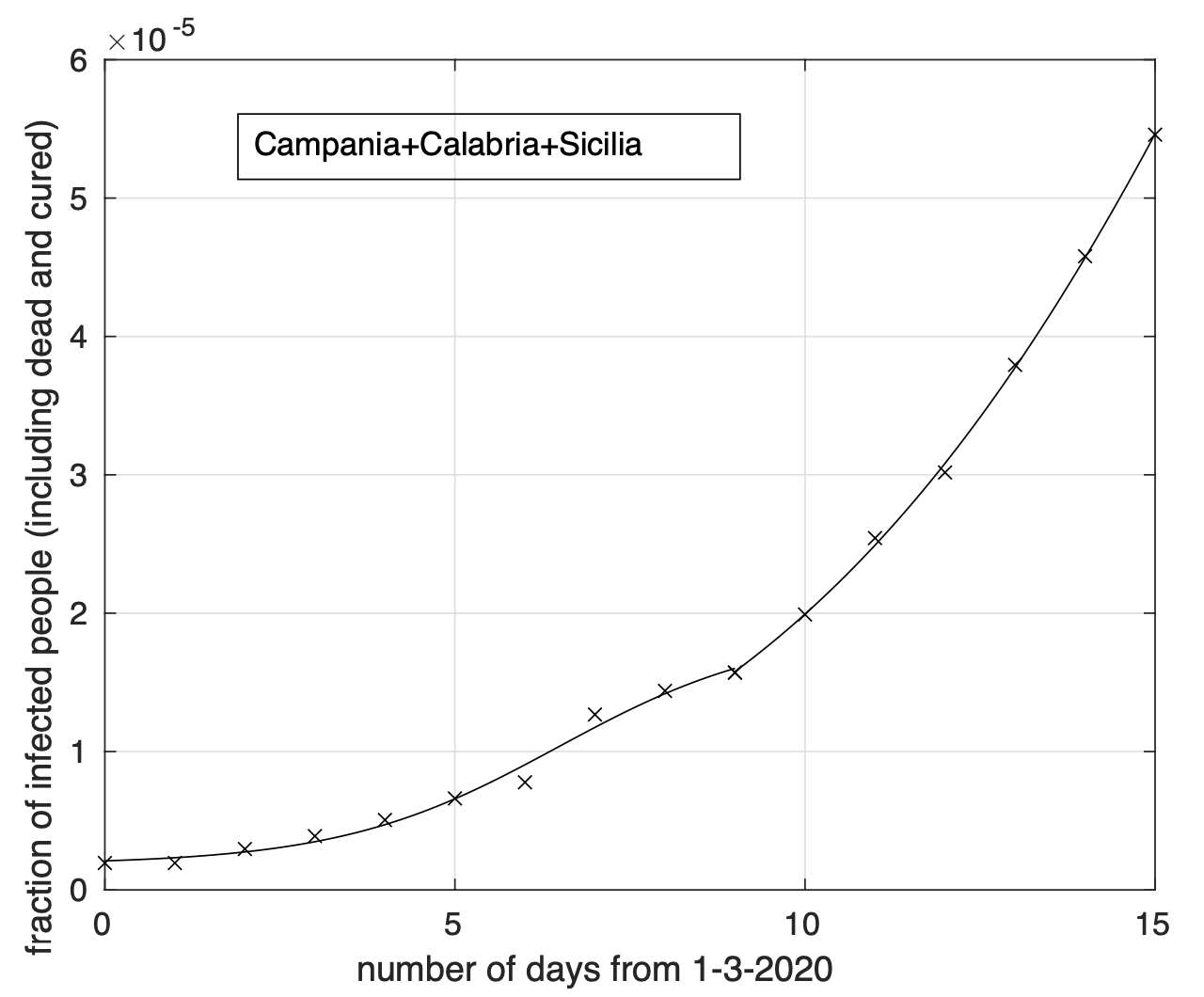
Figura 4. Frazione del numero di contagiati osservati nelle regioni del sud Italia: Campania, Calabria e Sicilia rispetto alla somma delle rispettive popolazioni in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello doppio logistico è sovrapposto ai dati.
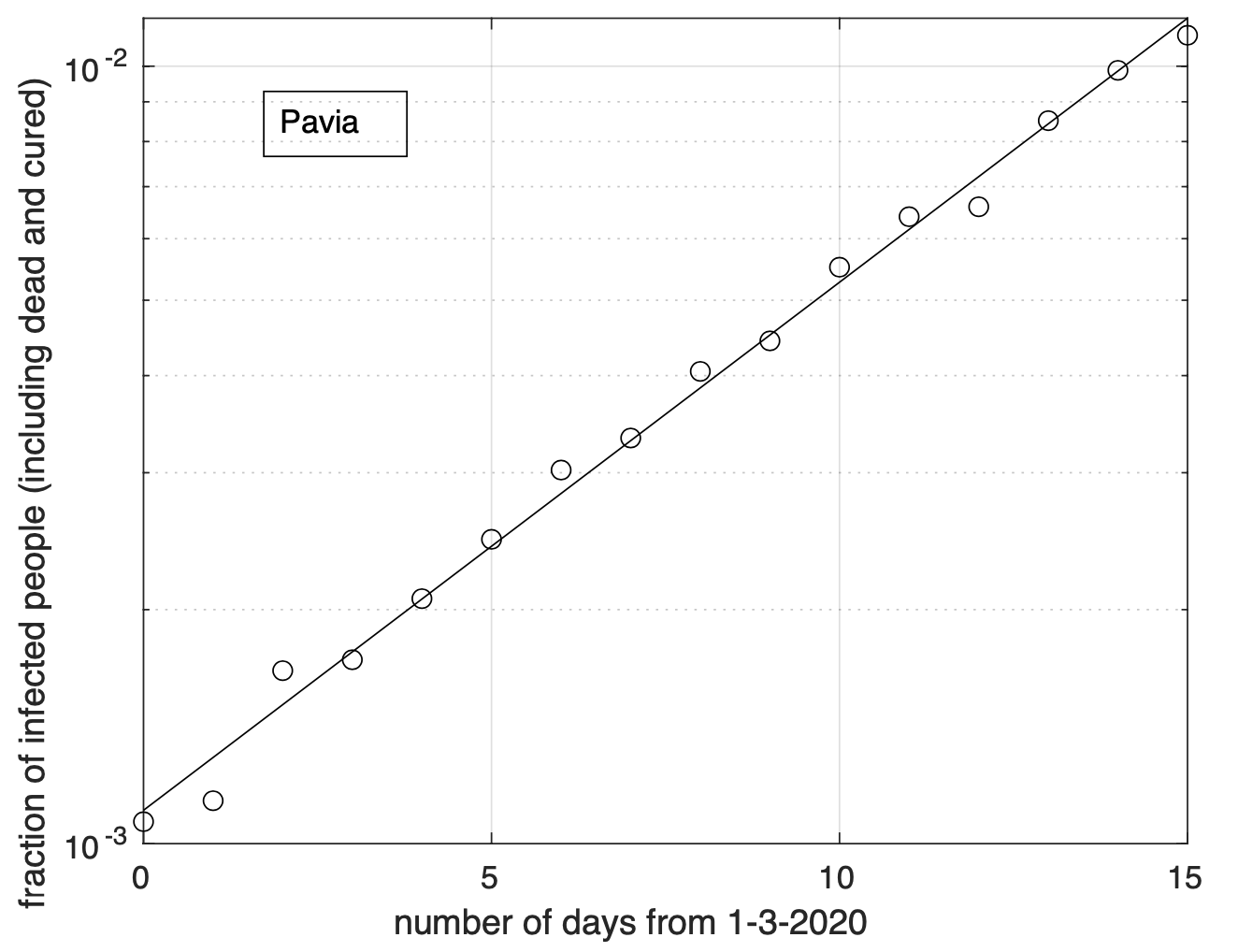
Figura 5. Sequenza temporale della frazione dei contagiati osservati nella provincia di Pavia rispetto alla popolazione della provincia (in scala semi-logaritmica). Il miglior fit con un modello geometrico è sovrapposto ai dati.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
Analisi dei dati epidemiologici del coronavirus in Italia (al 15 marzo)
- 10549 letture
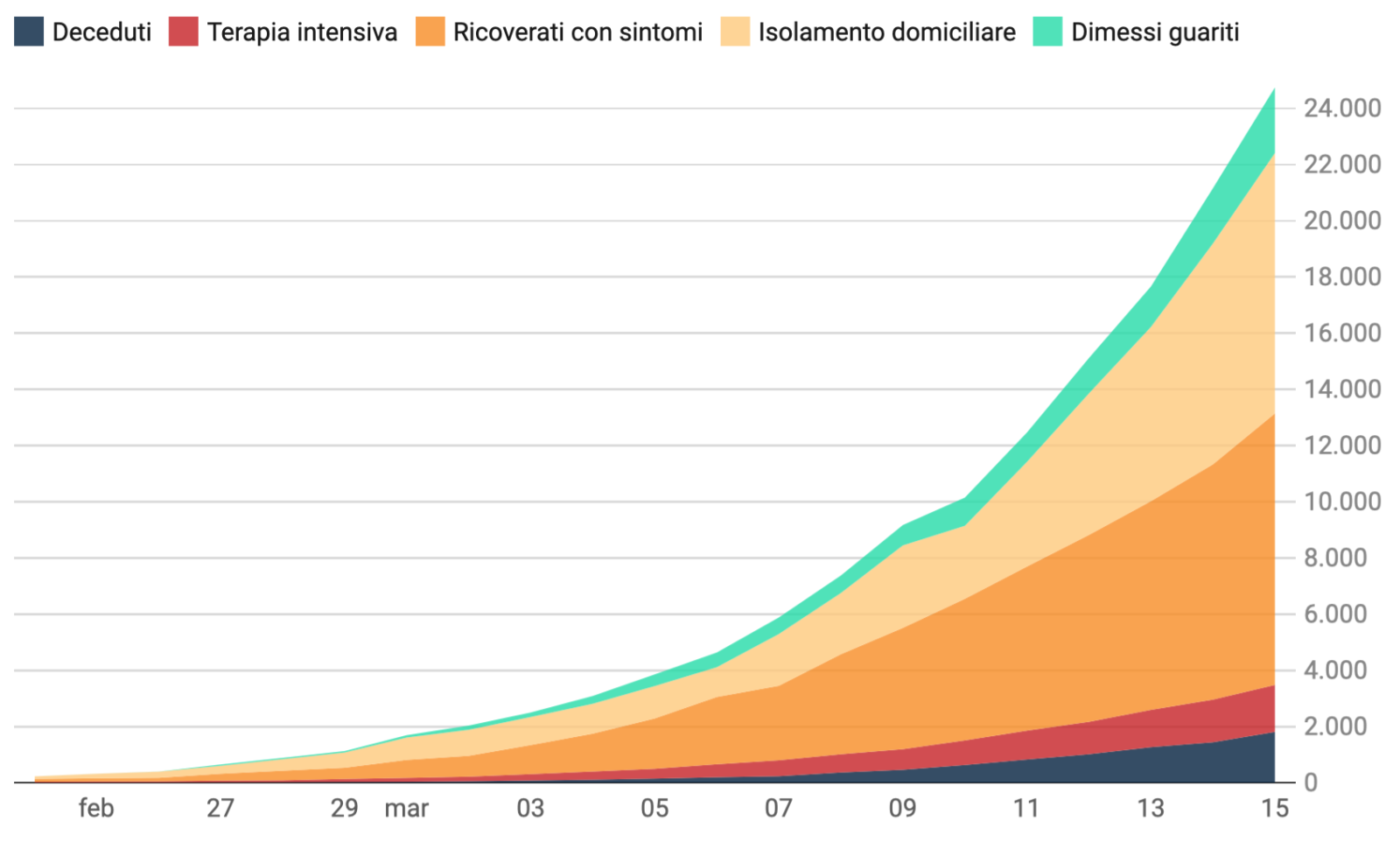
Presentiamo i risultati relativi all’analisi per la Lombardia, la Puglia e le sei province della Lombardia al momento maggiormente colpite, dei dati aggiornati alle 18 del 15 marzo 2020, che sostituiscono o integrano quelli nel documento del 14 Marzo. Vengono poi illustrati i risultati di un’analisi a livello nazionale su come l’epidemia si propaga all’interno del territorio italiano. I dati a livello regionale e nazionale sono stati scaricati dal sito https://github.com/pcm-dpc/COVID-19 e quelli a livello provinciale dal sito https://github. com/pcm-dpc/COVID-19/tree/master/dati-province.
Per quanto riguarda la Lombardia, si conferma anche per il 14-15 marzo la riduzione del tasso di crescita della frazione dei contagiati osservati relativa ai giorni 12-13 marzo e 13-14 marzo, come si può osservare in scala semi-logaritmica nella figura 1. Si spera che il trend si mantenga anche nei prossimi giorni.
Purtroppo, nelle regioni del centro-sud, ma più marcatamente in quelle del sud, persiste l’aumento del tasso di crescita della frazione dei contagiati osservati a partire dall’11 marzo dopo una precedente sua diminuzione, come già segnalato nel documento del 13 marzo e come si può vedere in figura 2 per la Puglia. Ribadiamo che la probabile principale causa di questo è l’esodo seguente il decreto che istituiva dall’8 marzo la zona rossa in Lombardia. Comportamenti come questo o come quello degli assalti ai supermercati prima che venissero introdotte delle modalità di accesso regolamentato sono da evitare perché inducono un aumento del rischio di contagio e di conseguenza contribuiscono alla diffusione dell’epidemia.
Per cinque delle sei province attualmente maggiormente colpite della Lombardia, Bergamo, Brescia, Cremona, Lodi, Milano e Pavia, è presente, come nei giorni precedenti, la dimuzione del tasso di crescita, esclusa Pavia. Infatti per Pavia l’adattamento del modello geometrico (che non presenta riduzione del tasso di crescita) ai dati è molto buono (vedi figura 3).
Descriviamo ora i risultati di un’analisi sul modo in cui l’epidemia di coronavirus si sta diffondendo all’interno del territorio italiano. Sappiamo che l’epidemia in Italia è iniziata a Bergamo. Abbiamo quindi preso Bergamo come punto di riferimento per la diffusione dell’epidemia. Fissato un giorno qualsiasi, abbiamo considerato i dati del numero di contagiati osservati in ciascun capoluogo di provincia fino a quel giorno. Per ciascuna capoluogo, abbiamo calcolato la sua distanza da Bergamo. Come distanza abbiamo scelto la lunghezza del cammino più breve, lungo la superficie di una sfera col raggio pari a quello terrestre (6.371 km), tra i due punti corrispondenti al capoluogo ed a Bergamo. Per il giorno considerato abbiamo quindi per ogni capoluogo la sua distanza da Bergamo e il numero di contagiati osservati al suo interno fino a quel giorno. Possiamo quindi calcolare la “distanza media” da Bergamo per quel giorno dei punti (capoluoghi) dove sono stati registrati casi di coronavirus fino ad allora. La media è di tipo pesato con i pesi proporzionali al numero di casi registrati per ciascun capoluogo fino a quel giorno. Come usualmente fatto nello studio del fenomeno della diffusione classica di particelle, la distanza media è calcolata prendendo la radice quadrata della media pesata del quadrato della distanza citata. Osserviamo che questa analisi non si occupa di studiare la diffusione dell’epidemia lungo particolari direzioni, ma considera tutte le direzioni assieme. In figura 4 mostriamo come varia la distanza media considerata al variare del tempo. Dal grafico vediamo che, a parte delle fluttuazioni di nessun significato, questa distanza aumenta nel tempo, con il tasso di crescita che aumenta anch’esso fino ad un massimo, per poi diminuire, esattamente come si comporta teoricamente la frazione dei contagiati osservati. Abbiamo perciò effettuato un fit con un modello logistico e il risultato è sovrapposto ai valori calcolati per la distanza media. Notiamo che il valore massimo del tasso di crescita è raggiunto attorno al 9 marzo, il giorno dopo l’introduzione della zona rossa in Lombardia. Seppure potrebbe essere una coincidenza, ipotizziamo invece che ci sia una relazione causa effetto. Per ora il fenomeno dell’esodo non trova riscontro qui e questo può essere dovuto al modesto aumento di nuovi casi di contagiati osservati nelle regioni del sud in seguito all’esodo e soprattutto all’istituzione della zona rossa in tutto il paese.
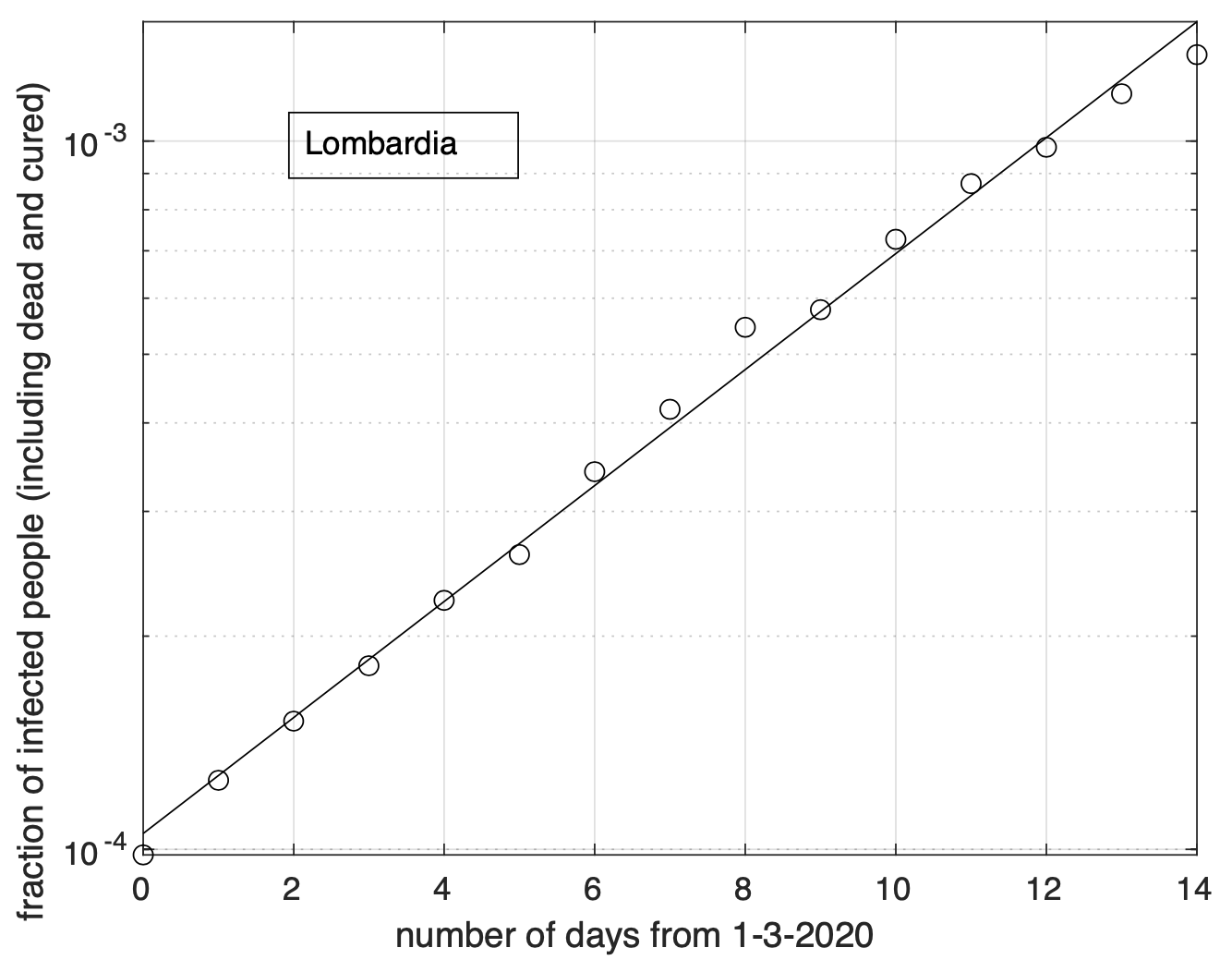
Figure 1. Frazione del numero di contagiati osservati in Lombardia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 Marzo ed in scala semi-logaritmica. La linea retta rappresenta il modello geometrico stimato a partire dai dati. Notiamo un buon adattamento del modello teorico ai dati e che gli ultimi tre punti sperimentali sono sotto la retta che corrisponde al miglior fit con un modello geometrico. Questo fornisce evidenza del trend di riduzione del tasso di crescita.
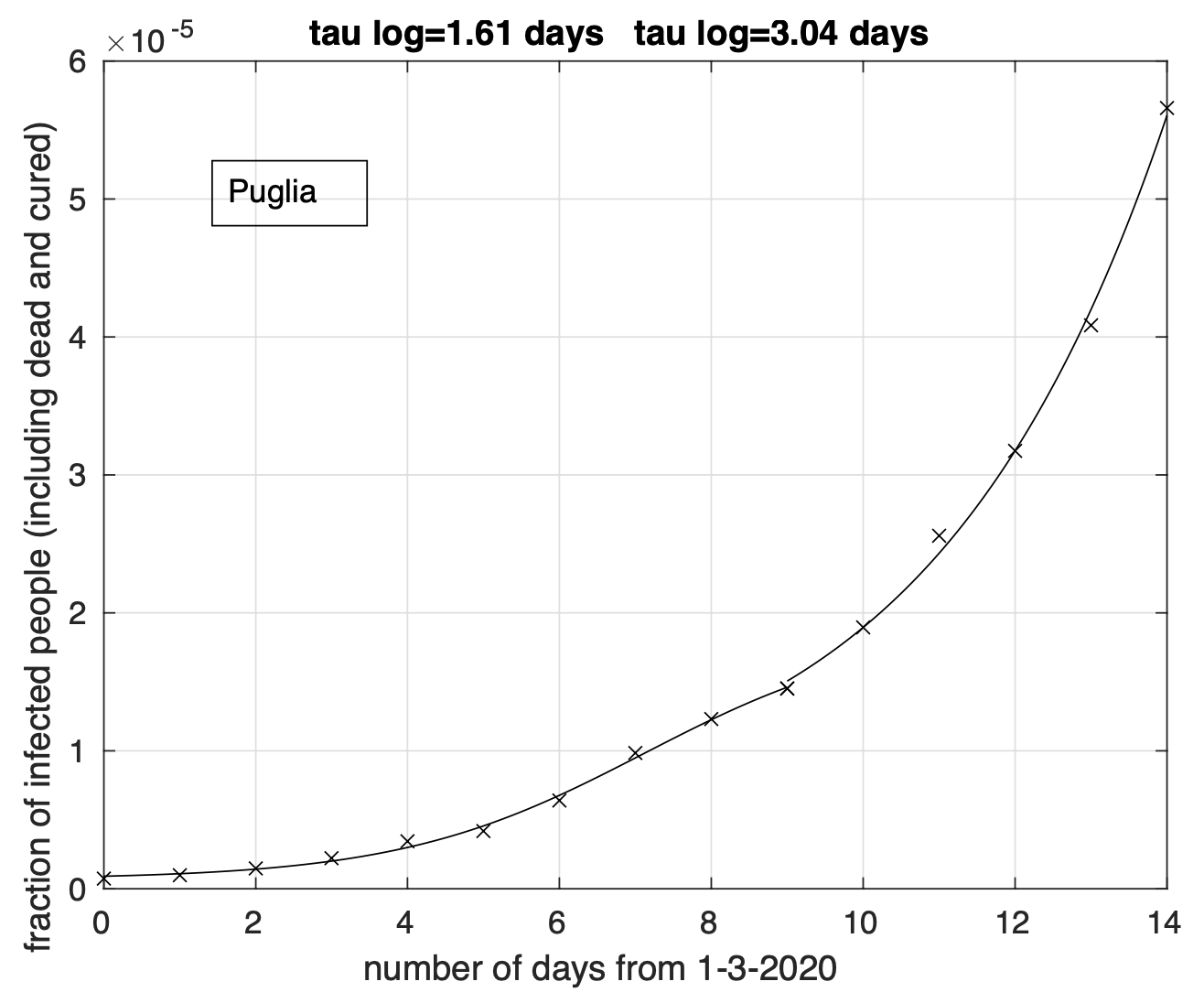
Figure 2. Frazione del numero di contagiati osservati in Puglia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo. Il miglior fit con un modello doppio logistico è sovrapposto ai dati.
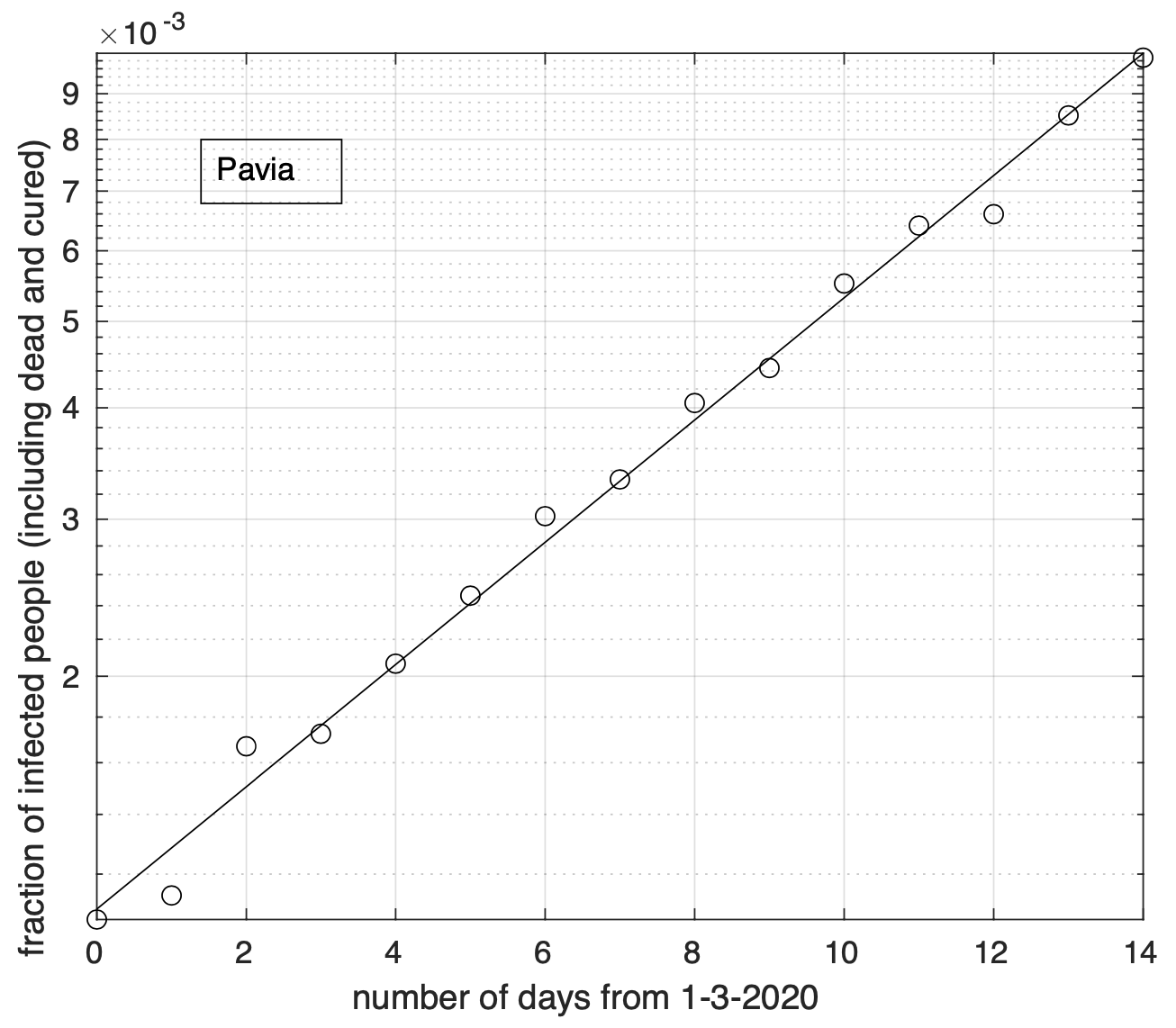
Figure 3. Sequenza temporale della frazione dei contagiati osservati nella provincia di Pavia rispetto alla popolazione della provincia (in scala semi-logaritmica). Il miglior fit con un modello geometrico è sovrapposto ai dati.
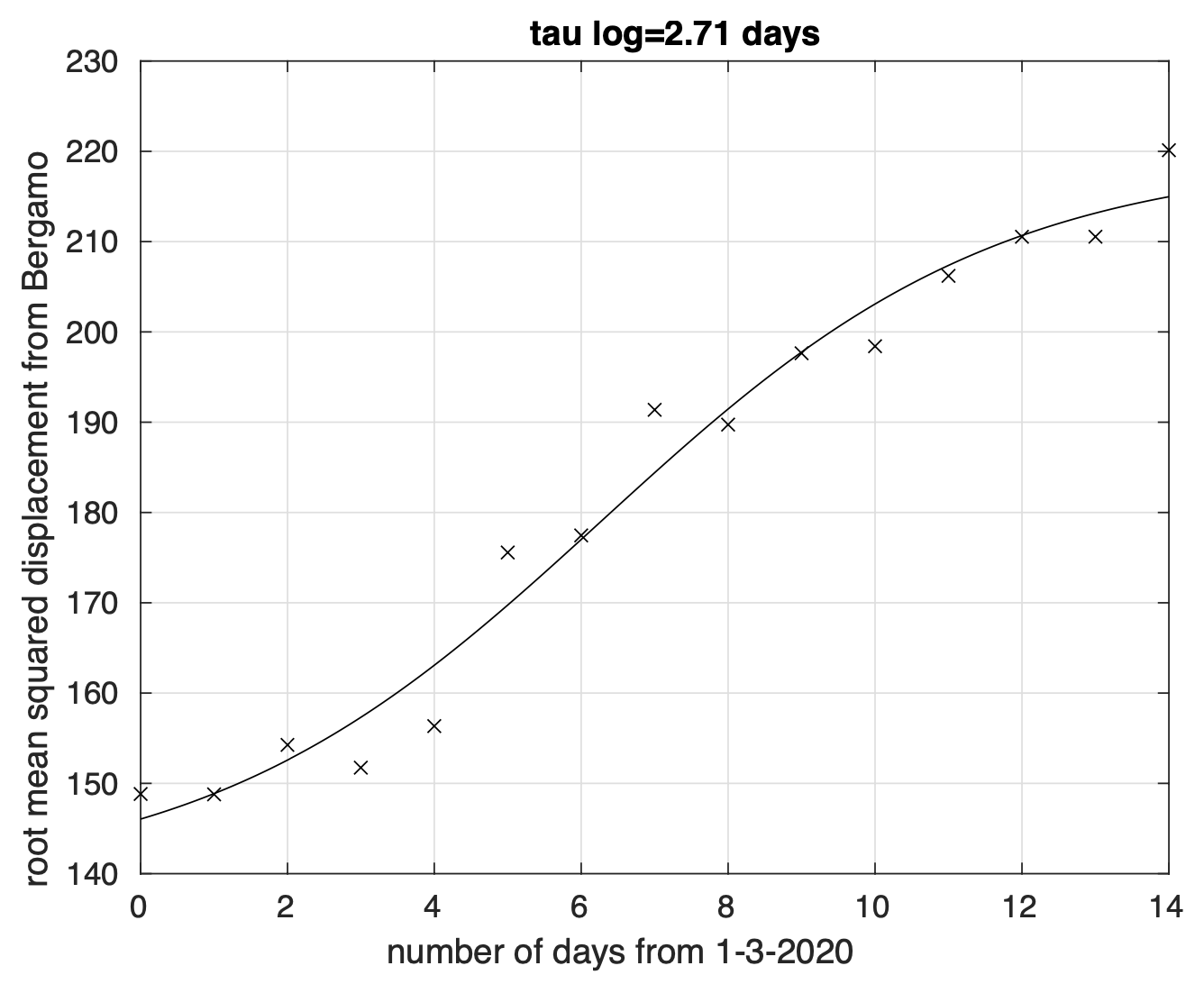
Figure 4. Andamento nel tempo della “distanza media” (in km) da Bergamo, origine della diffusione del coronavirus in Italia, dei punti del territorio italiano raggiunti dall’epidemia. Il miglior fit con un modello logistico è sovrapposto ai dati calcolati.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche
Analisi dei dati epidemiologici del coronavirus in Italia (al 14 marzo)
- 35832 letture
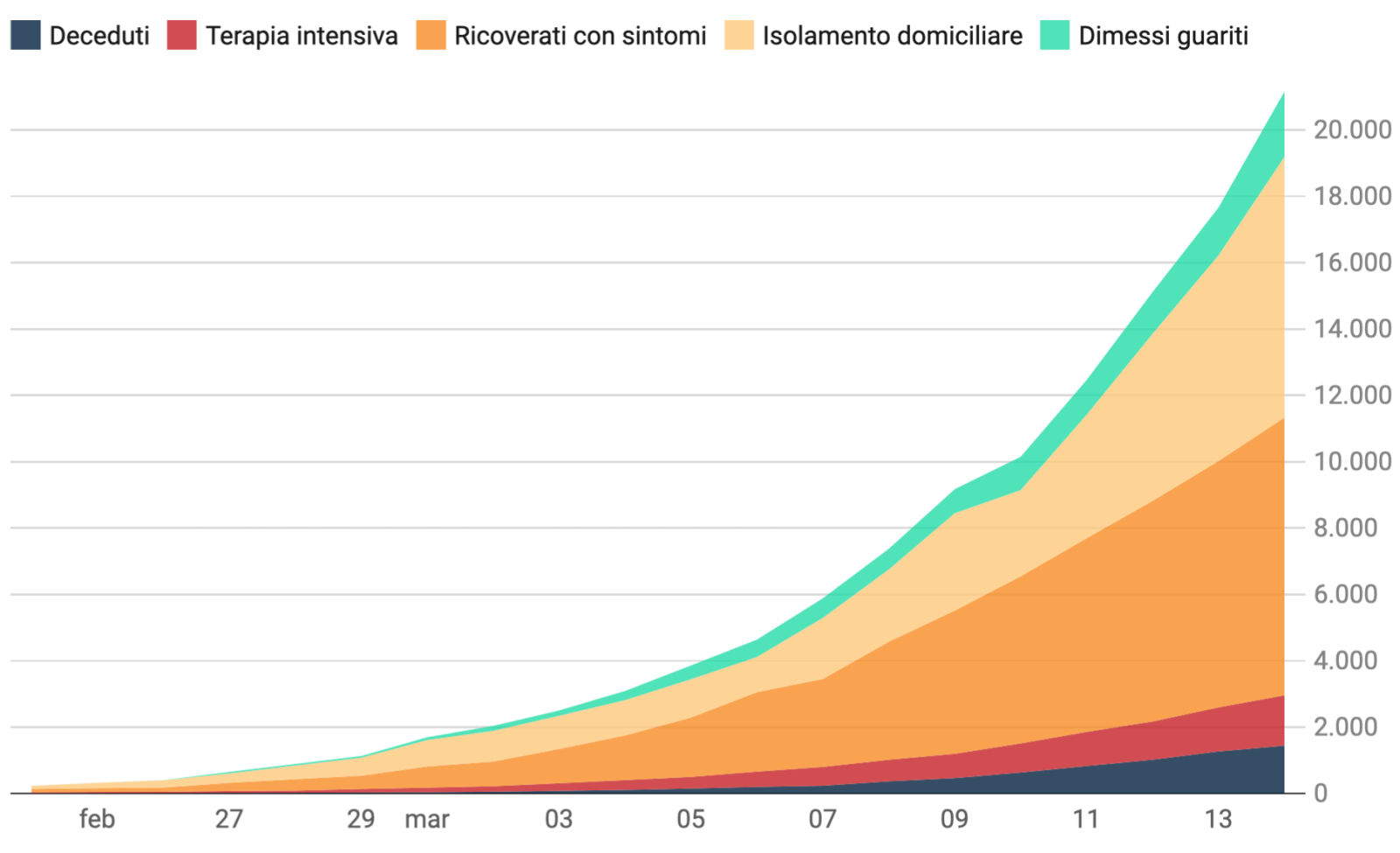
Illustriamo qui i risultati relativi all’analisi a livello regionale e delle sei province della Lombardia al momento maggiormente colpite dei dati aggiornati alle 18 del 14 marzo 2020, che sostituiscono o integrano quelli dell'analisi del 13 marzo. I dati a livello regionale sono stati scaricati dal sito https://github.com/pcm-dpc/COVID-19 e quelli a livello provinciale dal sito https://github.com/pcm-dpc/COVID-19/tree/master/dati-province. Sono stati inoltre analizzati i dati dell’epidemia del coronavirus in Cina. I dati in questo caso sono stati scaricati dal sito https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situatio....
Per quanto riguarda la Lombardia, si conferma anche per il 13-14 marzo la riduzione del tasso di crescita della frazione dei contagiati osservati relativa ai giorni 12-13 marzo, come si può osservare in scala semi-logaritmica nella figura 1. Si spera che nei prossimi giorni la riduzione del tasso venga ulteriormente confermata.
Sono stati stimati i valori del tempo dal 1 marzo a partire dal quale non si avranno praticamente variazioni della frazione dei contagiati osservati per le 15 regioni, esclusa la Lombardia, che a oggi sono maggiormente colpite (con numero dei contagiati effettivi maggiore di 50). Il valore medio di questi valori è 39 giorni, con errore standard della media pari a 4 giorni.
I risultati dell’analisi dei dati delle sei province della Lombardia attualmente maggiormente colpite, Bergamo, Brescia, Cremona, Lodi, Milano e Pavia, confermano quelli del 13 marzo. Infatti, tutte le province mostrano una dimuzione del tasso di crescita a parte Pavia, dove invece il modello logistico è equivalente a quello geometrico (vedi figura 2). La media dei valori del tempo dal 1 marzo a partire dal quale non si avranno praticamente variazioni della frazione dei contagiati osservati nelle 5 province (Bergamo, Brescia, Cremona, Lodi, Milano) è in questo caso uguale a 38 giorni.
In relazione ai risultati trovati per il tempo di stabilizzazione della frazione dei contagiati osservati, è interessante il confronto con il valore che abbiamo stimato a partire dai dati dell’epidemia del coronavirus in Cina (vedi figura 3). Infatti il valore stimato è pari a 40 giorni.
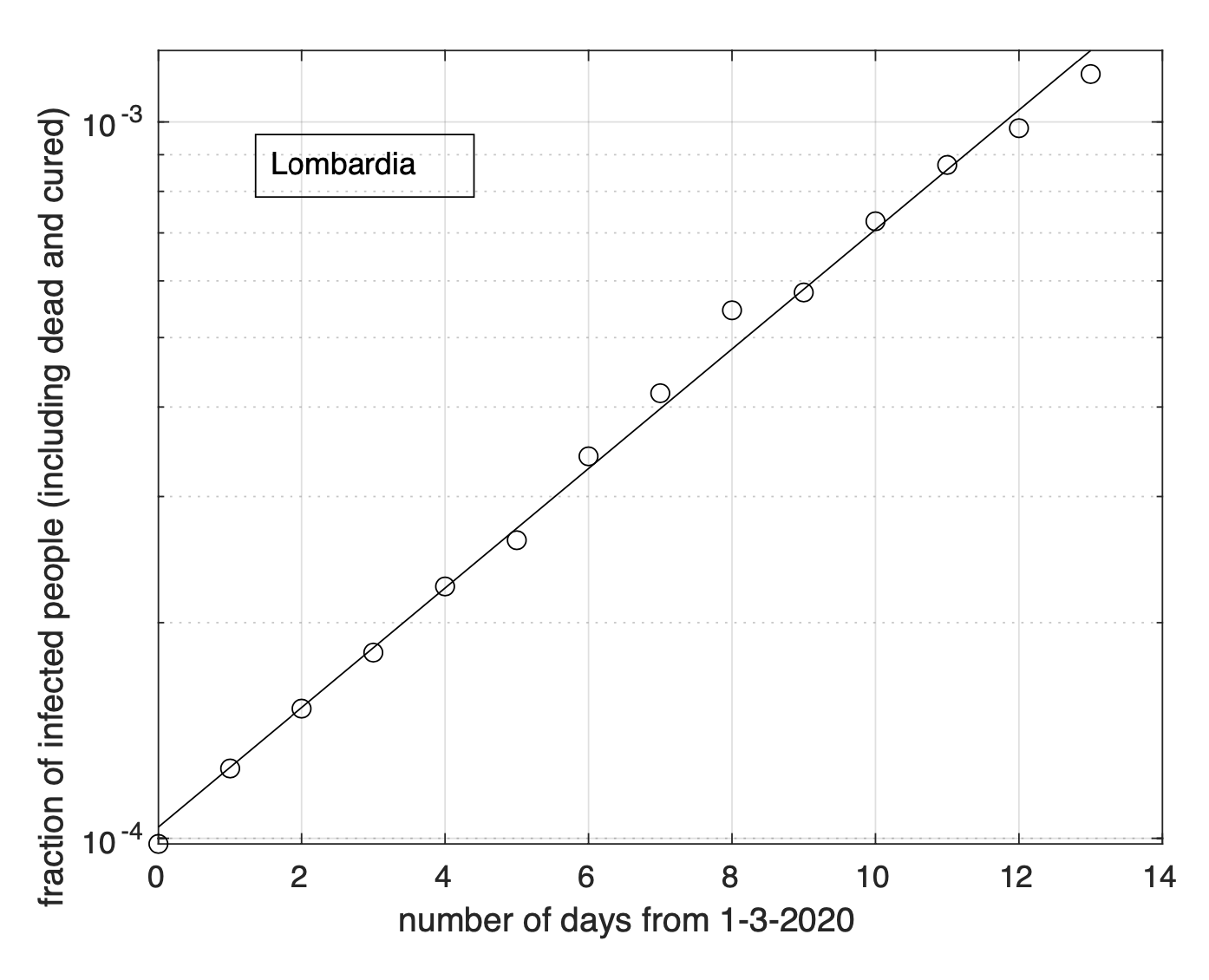
Figure 1. Frazione del numero di contagiati osservati in Lombardia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo ed in scala semi-logaritmica. La linea retta rappresenta il modello geometrico stimato a partire dai dati. Notiamo un buon adattamento dei dati al modello teorico.
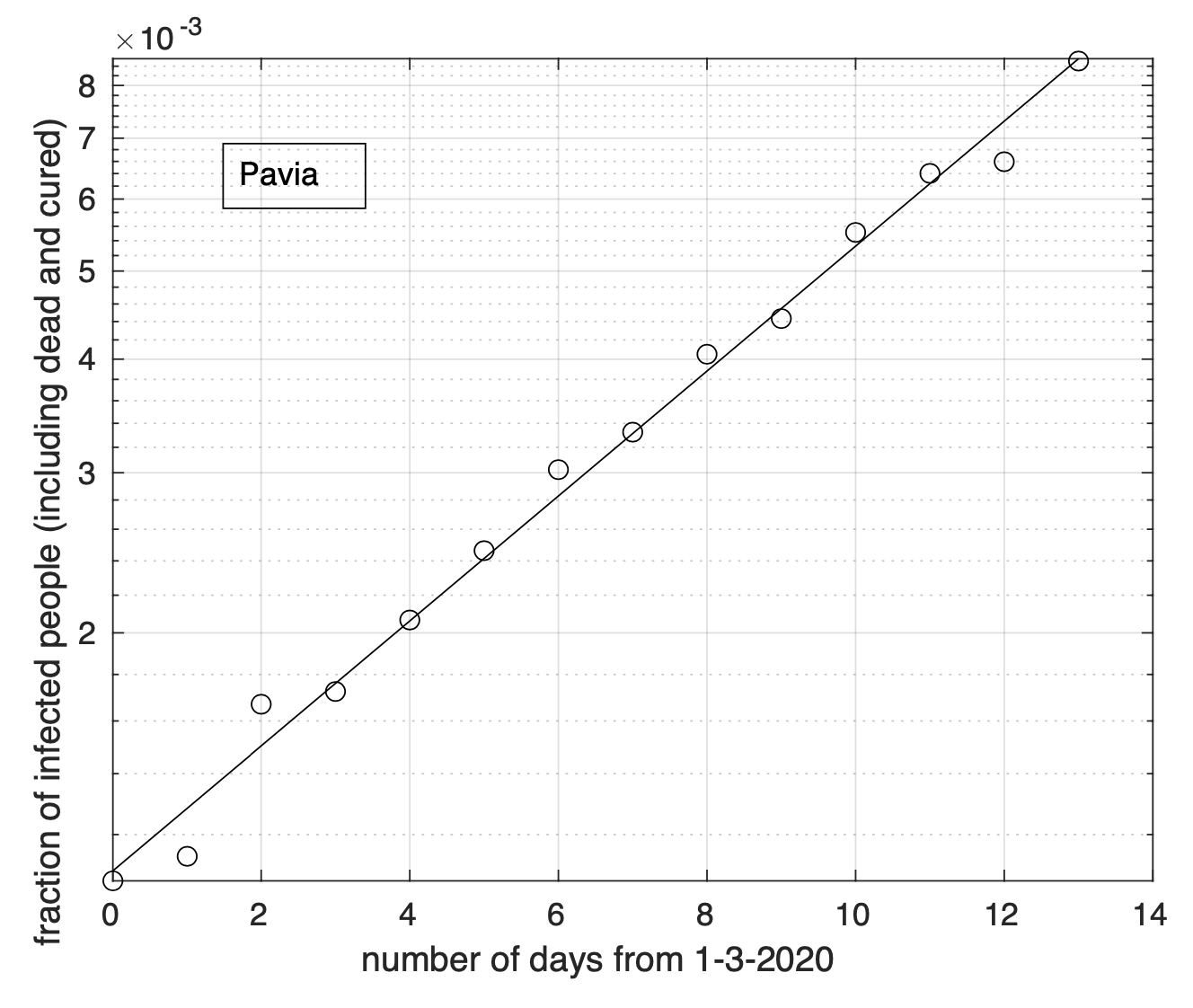
Figure 2. Sequenza della frazione dei contagiati osservati nella provincia di Pavia rispetto alla popolazione della provincia (in scala semi-logaritmica). Il miglior fit con un modello geometrico è sovrapposto ai dati.
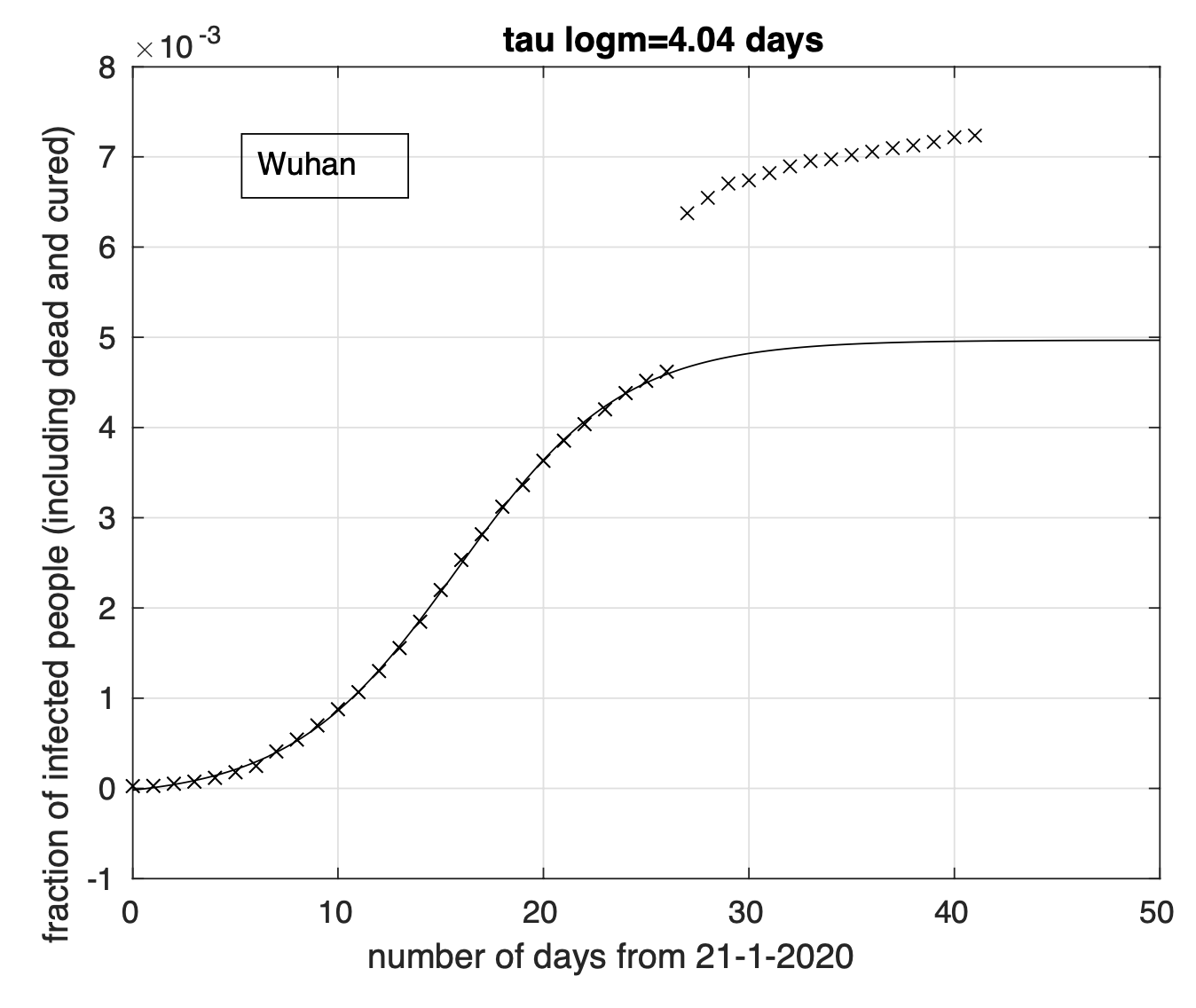
Figure 3. Frazione del numero di contagiati osservati in Cina (Wuhan) rispetto alla popolazione della zona considerata in funzione del tempo a partire dal 21 gennaio. La linea continua rappresenta il modello logistico stimato a partire dai dai misurati. Il salto presente nei dati avvenuto il 17 febbraio è dovuto al cambiamento di criterio per la diagnosi dei casi, che non era più basato su esami di laboratorio, ma solo su dati clinici.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "M. Picone", Consiglio Nazionale delle Ricerche
Analisi dei dati epidemiologici del coronavirus in Italia (al 13 marzo)
- 16073 letture
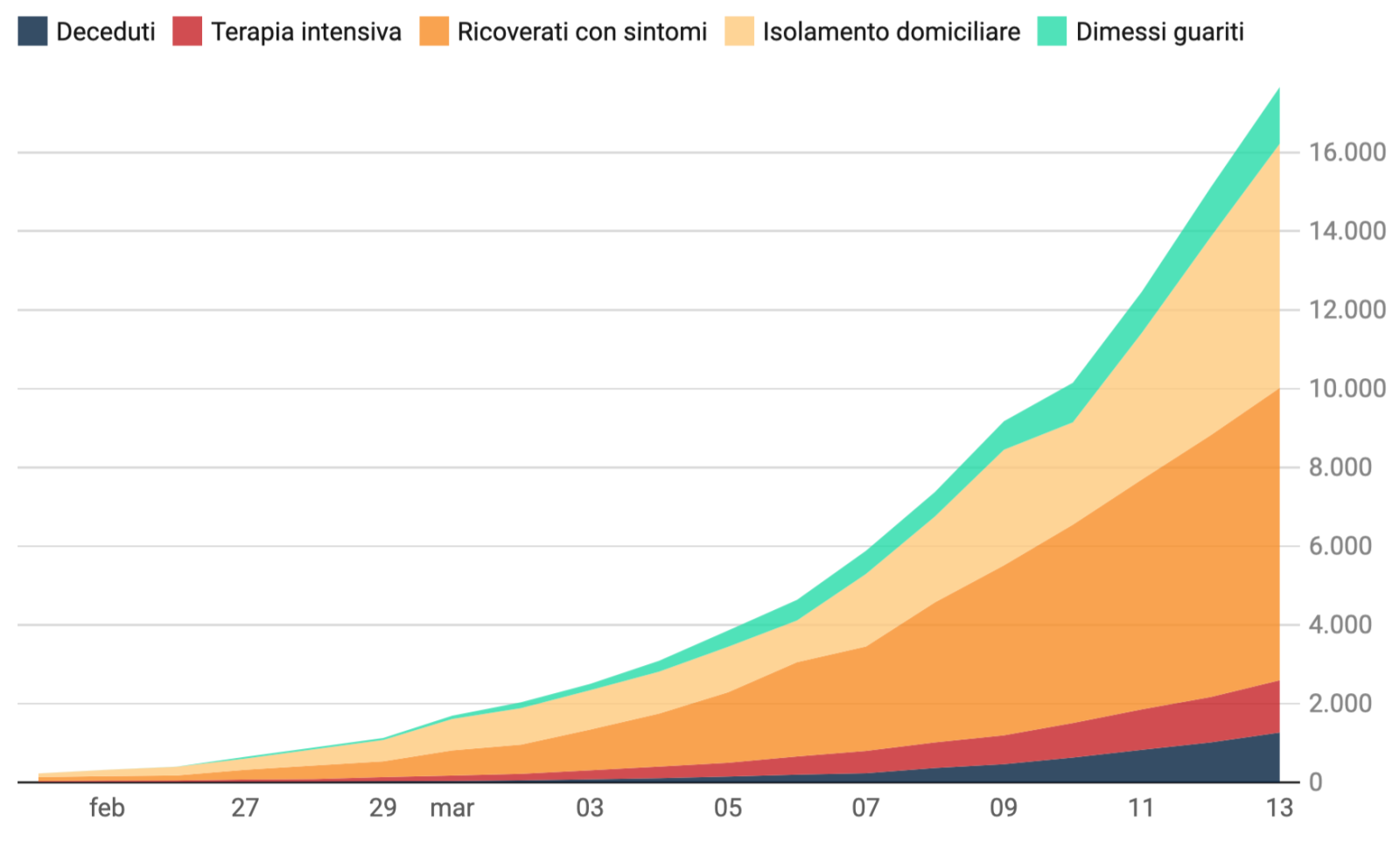
Illustriamo qui i risultati relativi all’analisi a livello regionale e delle sei province della Lombardia al momento maggiormente colpite dei dati aggiornati alle 18 del 13 marzo 2020, che sostituiscono o integrano quelli nel documento del 12 marzo. I dati a livello regionale sono stati scaricati dal sito https://github.com/pcm-dpc/COVID-19 e quelli a livello provinciale dal sito https://github. com/pcm-dpc/COVID-19/tree/master/dati-province.
Per quanto riguarda la Lombardia, osserviamo una riduzione del tasso di crescita della frazione dei contagiati osservati relativa ai giorni 12-13 marzo, come si può osservare in scala semi-logaritmica nella figura 1. Comunque, questo potrebbe essere dovuto ad un problema tecnico di conteggio, già accaduto il 10 marzo. Aspettiamo i prossimi giorni per una conferma della diminuzione del tasso.
Il range dei valori stimati del tempo dal 1 marzo a partire dal quale non si avranno praticamente variazioni della frazione dei contagiati osservati per il gruppo delle regioni Emilia, Veneto e Marche è 60-80 giorni. Per il gruppo delle regioni Toscana, Liguria e Trentino il range dei valori stimati è invece 20-40 giorni. Le altre due regioni del terzo gruppo dell’analisi del 12 marzo, Piemonte e Friuli, presentano un aumento del tasso di crescita relativo ai giorni 12-13 marzo, per cui sono state escluse dall’analisi col modello logistico. I prossimi giorni chiariranno la situazione.
Per quanto riguarda l’aumento del tasso di crescita a partire dall’11 marzo che segue una sua precedente diminuzione osservato precedentemente per le sequenze di Sicilia e Lazio e meno marcatamente per la Puglia è stato osservato anche nelle altre tre regioni con numero dei contagiati osservati maggiore di 50 per le quali abbiamo ora effettuato l’analisi: Campania, Abruzzo ed Umbria. In figura 2 vediamo la sequenza della frazione dei contagiati osservati cumulati in queste sei regioni rispetto alla somma delle loro popolazioni. Questo andamento è visibile in ciascuna delle sei regioni. Come già anticipato nel documento precedente, è possibile che questo aumento del tasso di crescita sia stato causato dall’esodo dal nord al sud avvenuto in seguito al decreto che l’8 marzo istituiva la zona rossa in Lombardia. Anche il fenomeno dell’assalto ai supermercati potrebbe avere delle ripercussioni nella diffusione dell’epidemia.
Abbiamo inoltre effettuato l’analisi dei dati delle sei province della Lombardia attualmente maggiormente colpite: Bergamo, Brescia, Cremona, Lodi, Milano e Pavia. Per i giorni considerati, dal 1 marzo al 13 marzo, rimangono alcune centinaia di casi della Lombardia (ma vale anche per altre regioni) che nel database non sono ancora assegnati a nessuna delle sue province. Abbiamo ignorato tali casi. L’analisi per le province di Brescia, Cremona e Lodi (vedi figure 3, 4 e 5) mette in evidenza una diminuzione del tasso di crescita, in particolare per quella di Lodi, forse a causa del suo miglior isolamento. Infatti l’adattamento ai dati del modello logistico è migliore che per il modello geometrico. Per la provincia di Pavia, (vedi Figura 6) l’adattamento dei due modelli è lo stesso. Per le restanti province di Bergamo e Milano (vedi Figure 7, 8), si ha un modesto miglior adattamento in corrispondenza del modello logistico.
In relazione al modello illustrato nel documento del 12 marzo, è utile sottolineare l’importanza della consistenza numerica dei portatori sani per la diffusione dell’epidemia. A supporto dell’ipotesi della presenza di una frazione non trascurabile di portatori sani nell’epidemia di coronavirus in Italia, c’è la ripetuta loro citazione, oltre a fattori demografici, da parte degli esperti delle istituzioni sanitarie nazionali per spiegare il significativo aumento del tasso di mortalità in Italia rispetto a quello in Cina. Infatti, ignorando il numero di portatori sani, il numero dei contagiati effettivi è sostituito dal più piccolo numero dei contagiati osservati. Questo diminuisce il denominatore nel calcolo della mortalità che risulterebbe in questo modo sovrastimata. Osserviamo che in questo contesto specifico, sono proprio i portatori sani i soggetti più rilevanti per la diffusione dell’epidemia. Infatti, i soggetti infettati che non sono portatori sani, sviluppano i sintomi in un tempo medio di 5 giorni circa, che sommato ad un tempo medio di diagnosi di 2 giorni, porta ad un tempo di una settimana circa in cui il soggetto può infettarne altri, essendo isolato in ospedale o a casa subito dopo la diagnosi. Un portatore sano invece, a meno che non abbia un ceto sociale elevato e sia sottoposto al test, non sa di esserlo e piò tranquillamente infettare altri soggetti. E quindi evidente l’importanza delle misure di limitazione della mobilità e più in generale quelle per la riduzione del rischio di infezione. Nel momento in cui il numero dei contagiati osservati rimarrà praticamente invariato, l’evoluzione dipenderà proprio dalla percentuale dei portatori sani. Se essa sarà non trascurabile, rimuovendo le misure di riduzione del rischio, sarà necessario lo sviluppo di una cura per evitare una ripartenza della diffusione e una decimazione selettiva, per età, della popolazione. Allo scopo di effettuare previsioni sulla diffusione dell’epidemia di coronavirus sulla base di modelli informativi, assieme a Marco Massa, dell’Imperial College, stiamo considerando un modello a compartimenti che tiene conto della presenza di portatori sani, il cui numero nel tempo costituisce una delle funzioni incognite. ll range dei valori stimati del tempo dal 1 marzo a partire dal quale non si avranno praticamente variazioni della frazione dei contagiati osservati per il gruppo delle province di Brescia, Cremona, Lodi, Bergamo e Milano è 30-50 giorni.
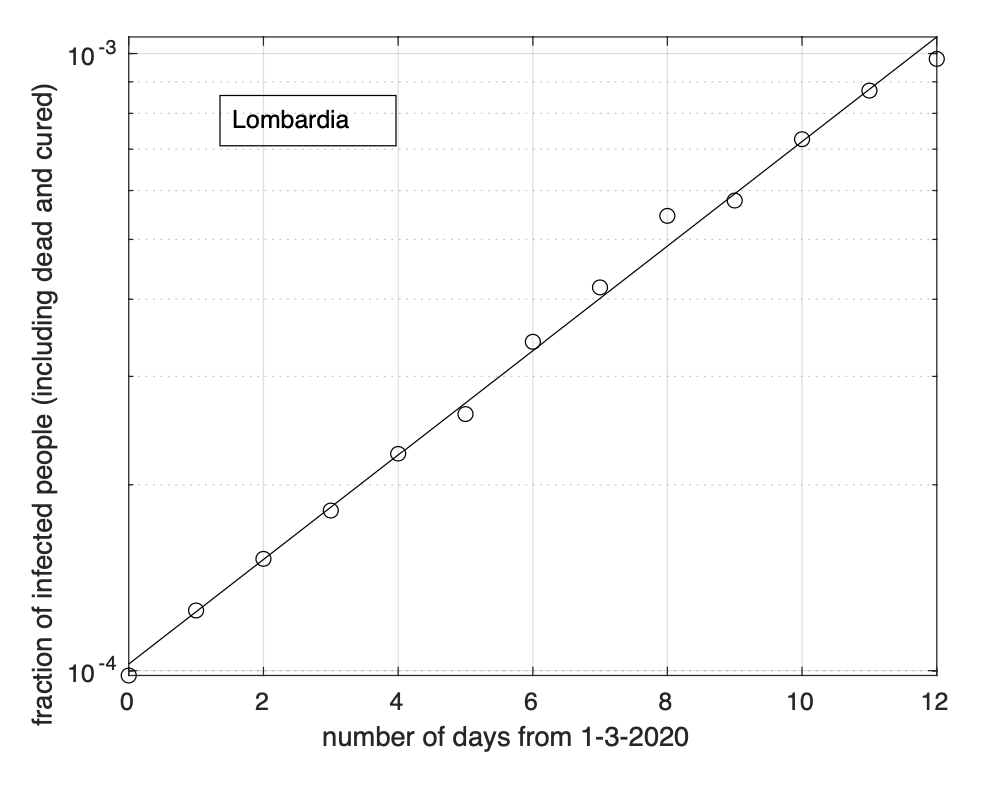
Figure 1: Frazione del numero di contagiati osservati in Lombardia rispetto alla popolazione della regione in funzione del tempo a partire dal 1 marzo ed in scala semi-logaritmica. La linea retta rappresenta il modello esponenziale stimato a partire dai dati. Notiamo un buon adattamento dei dati al modello teorico.
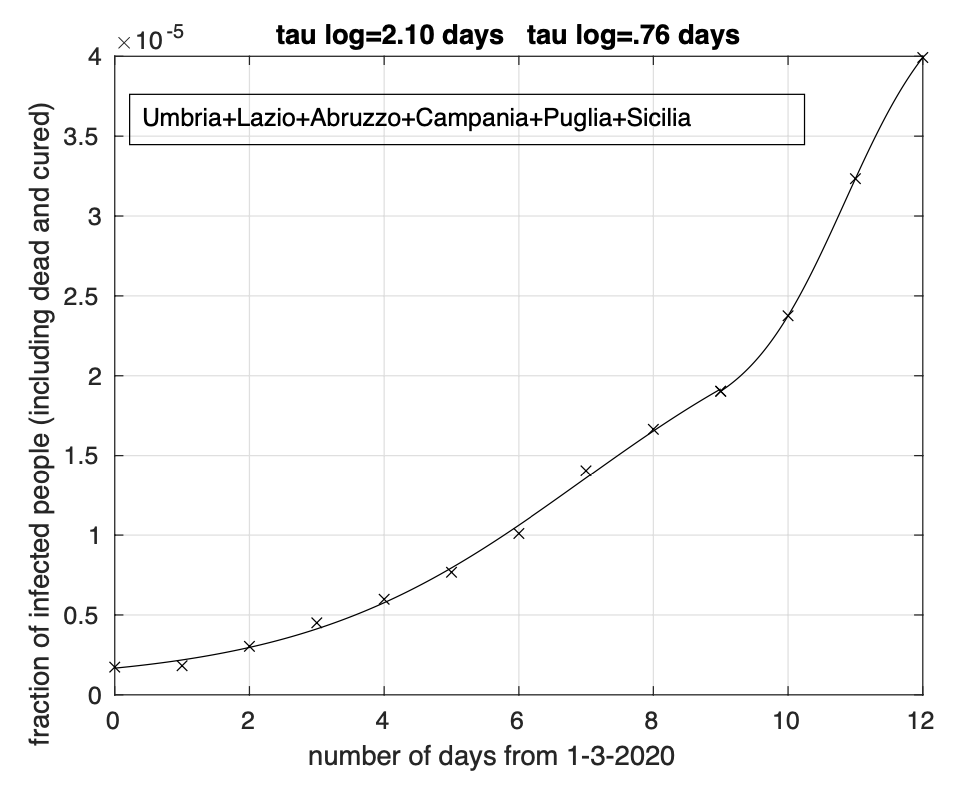
Figure 2: Sequenza della frazione dei contagiati osservati cumulati delle regioni Umbria, Lazio, Abruzzo, Campania, Puglia e Sicilia rispetto alla somma delle loro popolazioni. Il miglior fit con un modello doppio logistico è sovrapposto ai dati. Notiamo un aumento del tasso di crescita a partire dall’11 marzo dopo una sua precedente diminuzione.
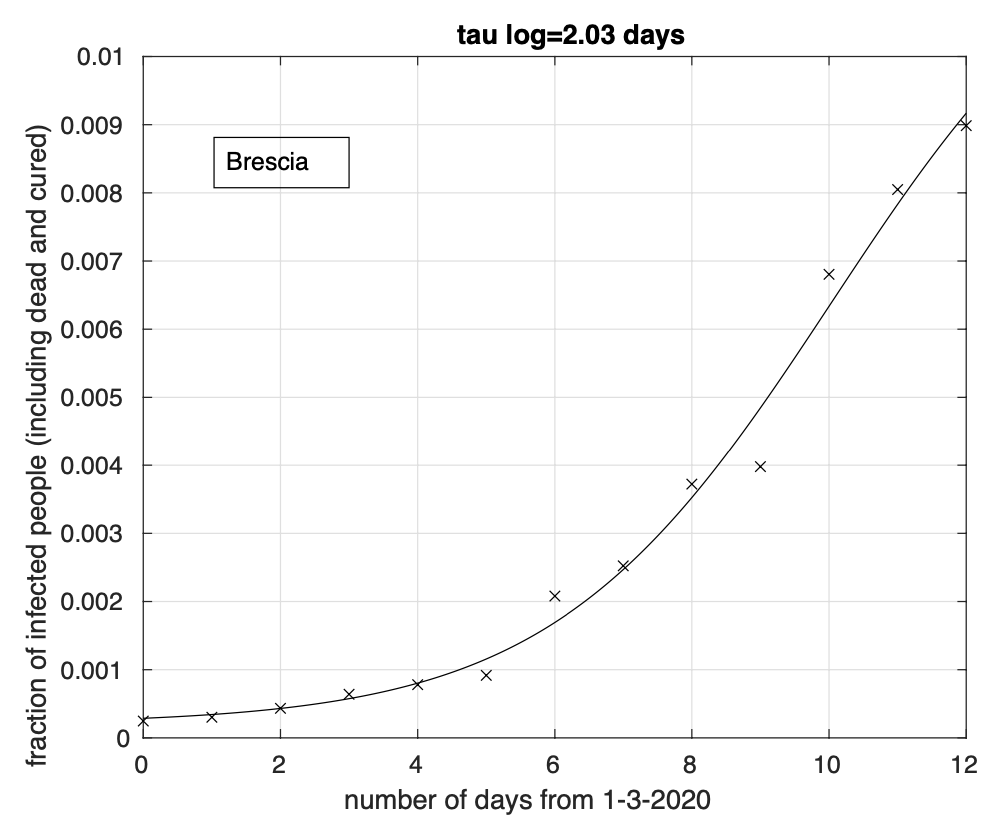
Figure 3: Sequenza della frazione dei contagiati osservati nella provincia di Brescia rispetto alla popolazione della provincia. Il miglior fit con un modello logistico è sovrapposto ai dati.
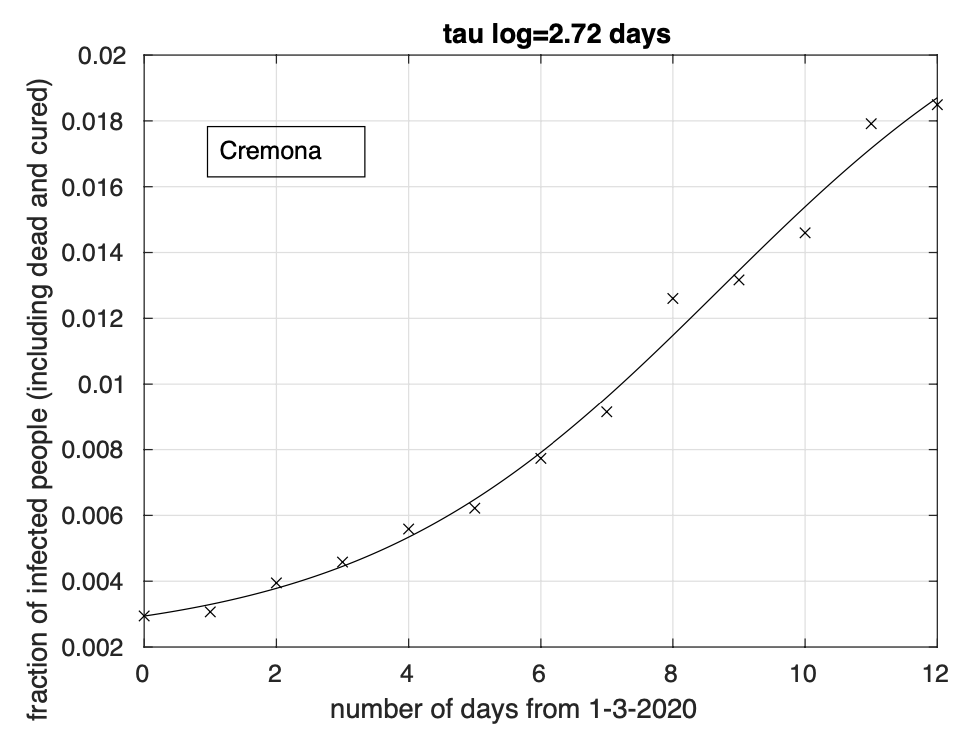
Figure 4: Sequenza della frazione dei contagiati osservati nella provincia di Cremona rispetto alla popolazione della provincia. Il miglior fit con un modello logistico è sovrapposto ai dati.
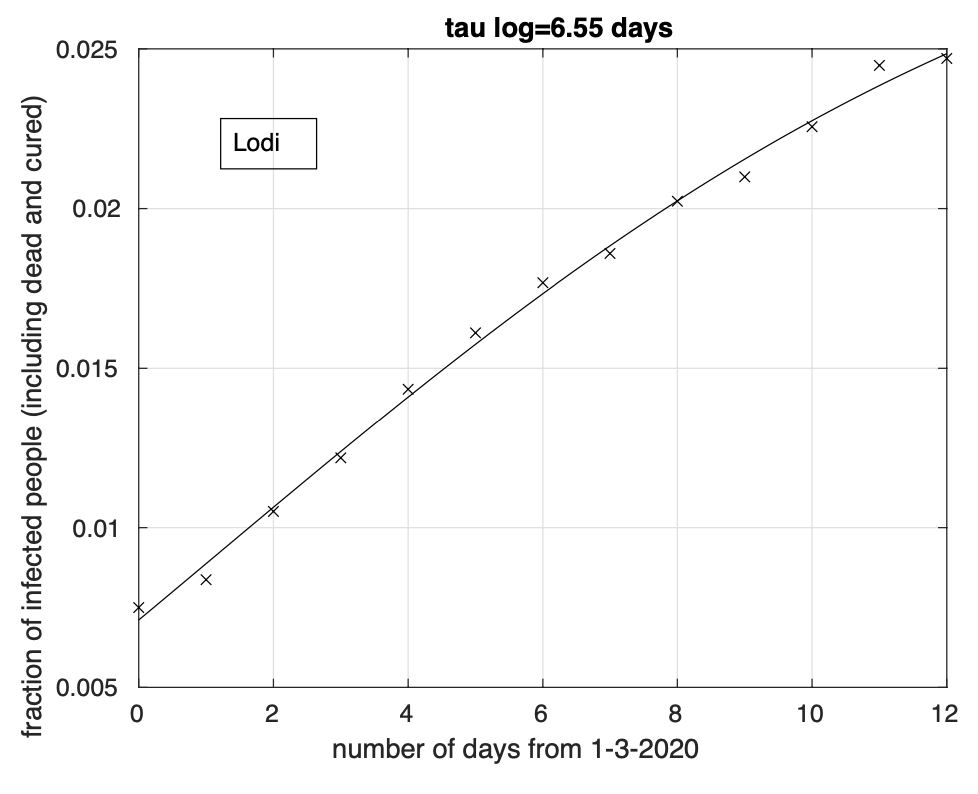
Figure 5: Sequenza della frazione dei contagiati osservati nella provincia di Lodi rispetto alla popolazione della provincia. Il miglior fit con un modello logistico è sovrapposto ai dati.
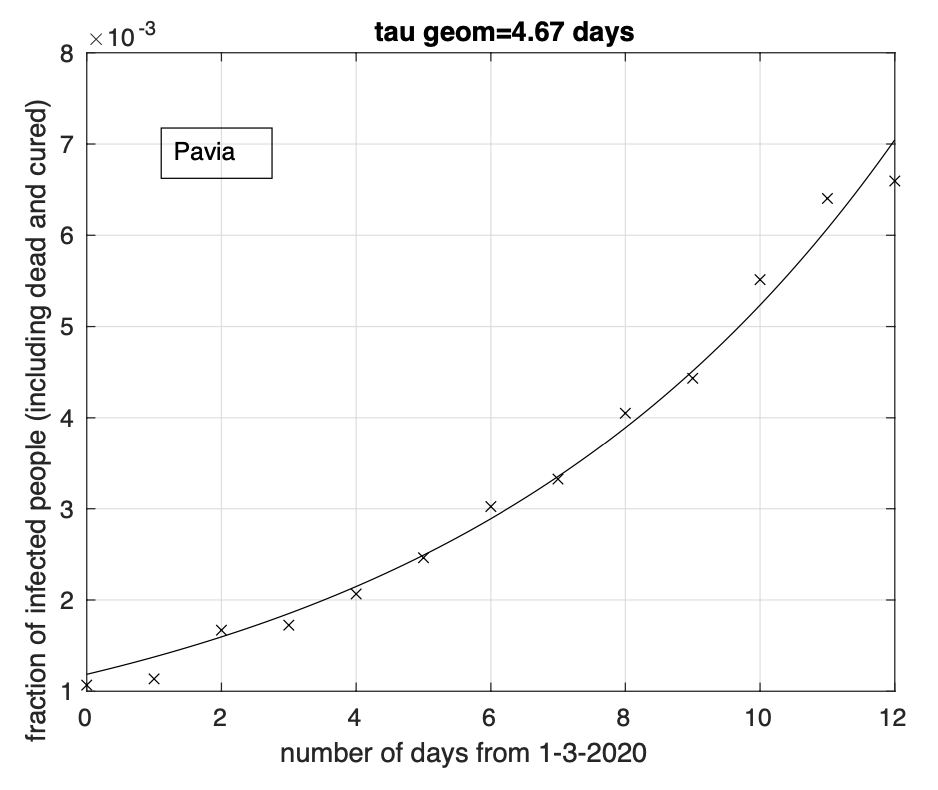
Figure 6: Sequenza della frazione dei contagiati osservati nella provincia di Pavia rispetto alla popolazione della provincia. Il miglior fit con un modello geometrico è sovrapposto ai dati.
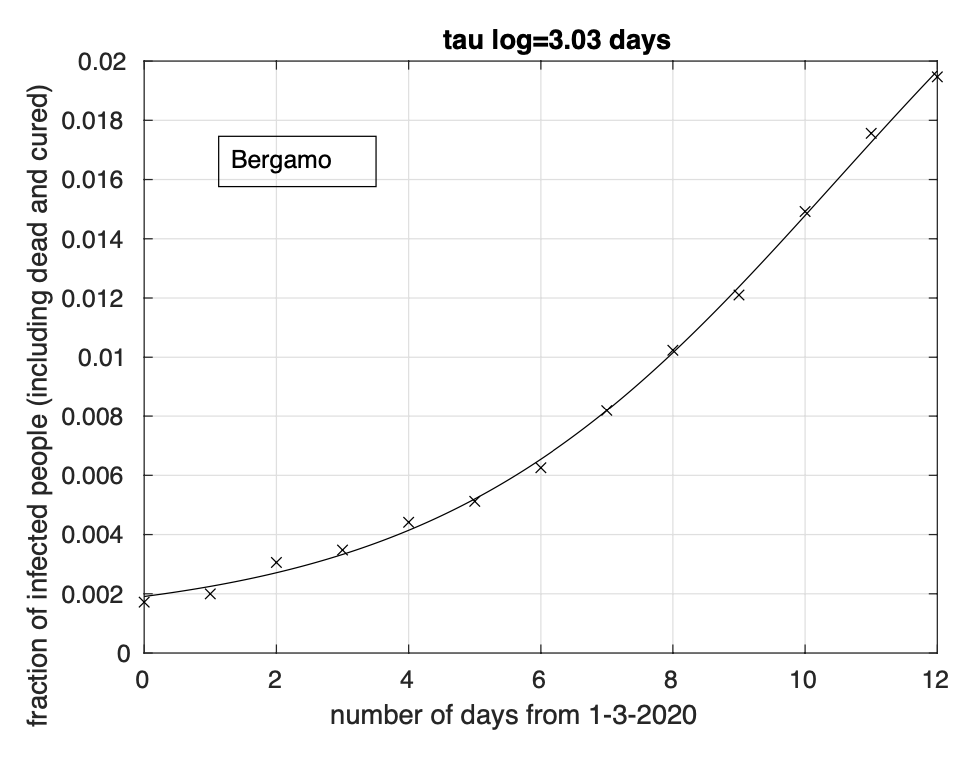
Figure 7: Sequenza della frazione dei contagiati osservati nella provincia di Bergamo rispetto alla popolazione della provincia. Il miglior fit con un modello logistico è sovrapposto ai dati.
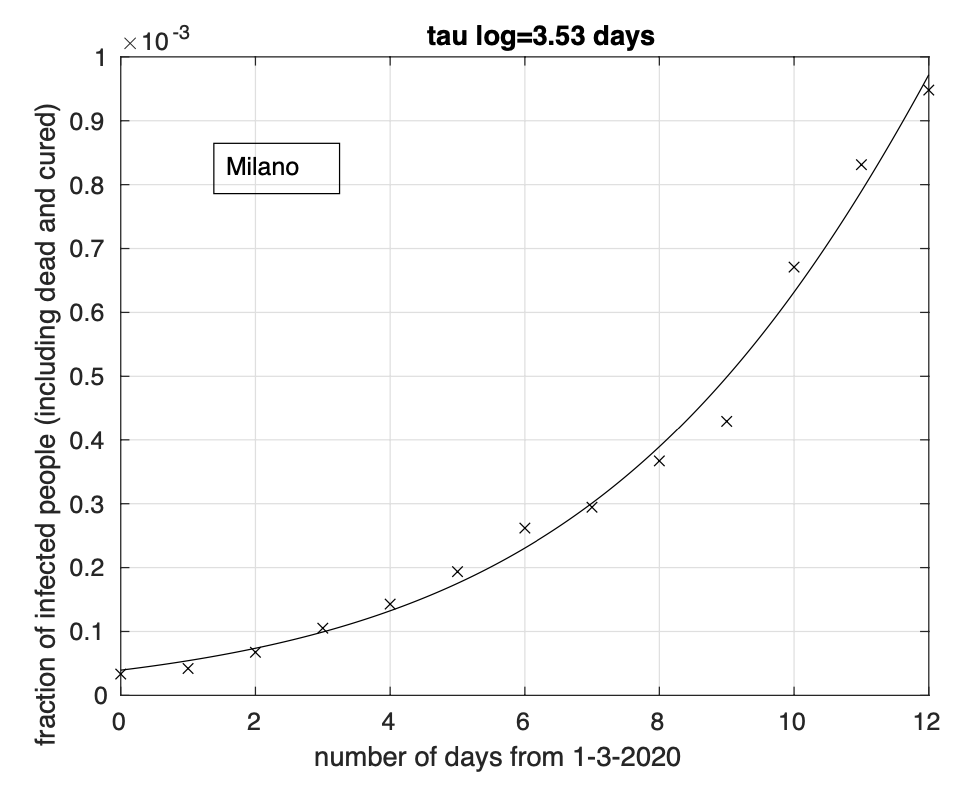
Figure 8: Sequenza della frazione dei contagiati osservati nella provincia di Milano rispetto alla popolazione della provincia. Il miglior fit con un modello logistico è sovrapposto ai dati.
Giovanni Sebastiani
Istituto per le Applicazioni del Calcolo "Mauro Picone", Consiglio Nazionale delle Ricerche