Ogni tanto ci sorprendiamo di vedere che degli eventi improbabili accadano: questi sono degli eventi straordinari in quanto si verificano raramente in quella che crediamo essere l'ordinaria realtà. Le grandi crisi economiche, come quella che stiamo vivendo, o altri eventi estremi, sono soprendendenti proprio perché si pensa che siano talmente improbabili che non si possano quasi mai verificare nella realtà. Il problema è dunque come valutare la probabilità che qualcosa avvenga, ed in particolare la distribuzione di probabilità di un certo fenomeno.

La scienza ha abbandonato da più di un secolo la visione determinista di Laplace e cerca di decifrare le regole che governano la casualità intrinseca dei fenomeni naturali da un punto di vista statistico. E' proprio da questo punto di vista che si cerca di interpretare le osservazioni e un'analisi statistica quantitativa fornisce gli appropriati quesiti teorici. Ci sono infatti due momenti differenti nella spiegazione di un certo fenomeno: quello dell'analisi statistica e quello successivo dell' interpretazione teorica in base a delle leggi conosciute. Tuttavia l'analisi statistica può essere fortemente influenzata dalle idee teoriche sottostanti e così il tipo di “domande” che si pongono ai dati e dunque il tipo di informazione che da questi si estrae per la successiva interpretazione teorica. Per fare un esempio, l'analisi dei mercati finanziari è molto (troppo?) spesso basata sulla ipotesi che le sottostanti distribuzioni di probabilità siano delle curve Gaussiane. In questo caso, il valore medio di un certo fenomeno (ad esempio il prezzo di un'azione) è ben denfinito così come la dispersione dei risultati (la varianza) intorno a questo. Ciò vuole dire che le code della curva gaussiana decadano così rapidamente da rendere quasi impossibili gli eventi che siano molto lontani dal valore medio (che in questo caso è anche il picco della probabilità, ovvero il valore più probabile). Dunque se si presuppone che i mercati finanziari (o altri fenomeni) abbiano un comportamento Gaussiano di fronte al verificarsi di eventi estremi la reazione non può che essere di sopresa e la conclusione è che si sia verificato un evento molto improbabile.

Si può poi discutere sulla probabilità che in un dato campione finito (il prezzo della nostra azione in un certo intervallo di tempo) si verifichi un evento così improbabile: certo a volte è anche possibile. Un'altra strategia consiste nel chiedersi se vi siano delle distribuzioni di probabilità non Gaussiane, che possano descrivere i dati in maniera più efficace. Dunque il punto chiave sta proprio nell'assegnare le probabilità agli eventi che non siano basate su delle ipotesi a priori (o, peggio, su dei pregiudizi ideologici) ma che invece siano corroborate dall'analisi empirica.

La distribuzione di Gauss ha una particolare importanza che deriva dal Teorema del Limite Centrale secondo cui la somma di variabili casuali che soddisfano certe proprietà, si distribuisce proprio secondo la curva di Gauss. Tra le altre vi è una particolare proprietà che si richiede: l'assenza di correlazioni a lunga portata tra le variabili casuali stesse, ovvero che due eventi sufficientemente lontani (nello spazio e/o nel tempo) possano essere considerati come independenti. Questo non è sempre vero: ad esempio durante le crisi finanziarie avvengono dei “moti collettivi” per cui tanti operatori che in situazione “di regime” operano secondo il loro giudizio personale, e dunque in maniera indipendente, fanno la stessa cosa (ad esempio vendono un'azione o la comprano tutti insieme nello stesso momento). Questo fenomeno collettivo equivale all'apparizione di una correlazione a lunga portata. Quando gli eventi sono di questo tipo, le ipotesi su cui si basa il Teorema del Limite Centrale non sono più valide e si aprono le porte al “selvaggio” mondo dei fenemoni con grandi fluttuazioni.

In questo caso non ci sono dei teoremi limite analoghi al caso del Teorema del Limite Centrale, e le distribuzioni di probabilità risultanti possono essere le più diverse. Queste hanno però, in genere, una caratteristica comune, quella di avere delle code lunghe, che decadono molto lentamente in funzione della distanza dal picco di probabilità. Questo significa che eventi molto lontani dal picco della distribuzione (il valore più probabile) hanno una probabilità di verificarsi non trascurabile contrariamente al caso delle Gaussiane. Vi sono anche dei casi in cui la media e la varianza possono divergere e dunque non ha più senso chiedersi quale sia il valore medio di una certa variabile o la sua dispersione.

Per fare un esempio semplice concentriamoci solo sulla forma della distribuzione di probabilità. Abbiamo contato quante volte sia citato un articolo pubblicato negli anni 1982-2006 sulla rivista Physical Review Letters (vedi figura 1) ed abbiamo diviso il numero di articoli con un certo numero di citazioni per il numero totale di articoli (ovvero abbiamo stimato la probabilità che un articolo abbia un certo numero di citazioni). Si nota dalla figura che il valore medio non rappresenta una quantità significativa per questa distribuzione. Questo viene infatti fissato dalla coda: anche pochi articoli che sono citati molto spesso possono cambiarne il valore. Se considerassimo un intervallo di tempo più lungo di 25 anni esaminati, troveremmo una media spostata verso valori più grandi. Come si vede dalla figura una distribuzione di Gauss ha un andamento completamente diverso dai dati: è molto stretta intorno al valore medio e non è dunque in grado di cogliere l'importanza degli articoli con tante citazioni (ovvero la coda della distribuzione).

Dunque, in questa situazione le domande che un'analisi statistica appropriata si pone sono diverse da quelle che sorgono spontanee quando si interpretano i fenomeni con la concezione apriori che questi siano gaussiani. Cosi' saranno diversi gli “osservabili” che saranno oggetto di una successiva interpretazione teorica. Non ci sono dei comportamenti universali nei fenomeni con grandi fluttuazioni ma vi è una sempre vivace ricerca di casi limiti e “classi di universalità” ovvero di fenomeni che sono caratterizzati da un certo tipo di correlazione a lunga portata e che danno luogo a distribuzioni di probabilità simili. Si perde la certezza del Teorema del Limite Centrale, e ci si avventura in un mondo sconosciuto ma proprio per questo ricco di soprese e di problemi aperti.

Figura 1

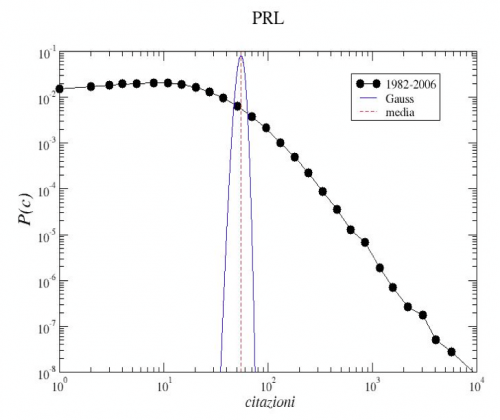
Sull'asse x vi è il numero di citazioni c e sull'asse y il numero di articoli che hanno ricevuto c citazioni diviso il numero totale di articoli. La curva in blu è una Gaussiana centrata sul numero medio di citazioni per articolo (linea rossa tratteggiata)

Per saperne di più
Theory of Financial Risks Jean-Philippe Bouchaud and Marc Potters Cambridge University Press 2003 Cap.1 disponibile in rete su http://lanl.arxiv.org/abs/cond-mat/9905413v1 ed per il Teorema del Limite Centrale http://en.wikipedia.org/wiki/Central_limit_theorem