Semplice e significativo esperimento sul concetto di variabile dell’insegnante Michela Rossetti della media di Appignano.

Nell’ambito di un progetto di studio sulla fisica dei suoni, Michela ha guidato i suoi allievi della 2ª C alla costruzione di uno strumento in legno, con sei corde di nylon, il suonometro.

Lo strumento è stato costruito per rispondere al seguente problema sperimentale:

Da cosa dipende l’altezza del suono prodotto dalle vibrazioni di una corda tesa?

Si sono considerate tre variabili indipendenti (tensione, spessore e lunghezza delle corde) e una variabile dipendente (l’altezza del suono prodotto quando si pizzicano tali corde).

Le corde sono state realizzate con fili da pesca di due sezioni diverse.

Come si vede dalla foto, le prime due corde da sinistra differiscono per la diversa tensione (ottenuta applicando dei pesi che agiscono verticalmente sulla parte libera). Quella più tesa produce un suono più acuto. La seconda e la terza hanno lo stesso peso e la stessa lunghezza, ma differiscono in spessore. Quella più spessa produce un suono più grave. Per le altre tre corde, di identica sezione e con lo stesso peso applicato, la lunghezza è decrescente e producono di conseguenza suoni di altezza crescente.

Si conclude che l’altezza del suono (rivelatrice della frequenza di vibrazione) è correlata positivamente alla tensione delle corde e inversamente alla loro lunghezza e al loro spessore.

Foto del”suonometro” durante la mostra del 6 maggio

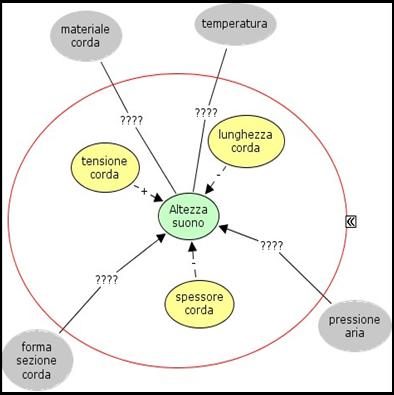
Diagramma per lo studio dei fattori che influenzano l’altezza del suono prodotto dalle corde del suonometro

Un po’ di teoria

La teoria delle oscillazioni prevede, per una corda fissata a due estremità, una frequenza di oscillazione fondamentale pari a  (espressa in hertz, cioè oscillazioni complete al secondo).

In questa formula L è la lunghezza della corda, r è la densità lineare, cioè la massa di una sua lunghezza unitaria (ci dice quanto è pesante la corda e a parità di materiale è proporzionale all’area della sezione) e T è la tensione della corda a riposo, pari al peso che la tiene tesa.

I risultati trovati rispecchiano la formula perché:

1. Se si dimezza la lunghezza la frequenza (e l’altezza) si raddoppia.

2. Se si aumenta la tensione T la frequenza aumenta (anche se non in proporzione diretta)

3. Se si aumenta la “pesantezza” o lo spessore della corda, la frequenza diminuisce (anche se non in proporzione inversa)

Come migliorare l’esperimento

Innanzitutto occorrerebbe mettere un “ponticello" sottile in corrispondenza della piegatura delle corde (come in una chitarra).

Secondariamente il suono diverrebbe meglio udibile costruendo una cassa di risonanza.

Si potrebbe quindi realizzare un ponticello mobile in modo che la lunghezza della corda possa variare con continuità.

Sarebbe eccezionale poter misurare le frequenze di vibrazione con un apparecchio accordatore digitale e le tensioni con una bilancia sensibile al grammo. Si potrebbe verificare così la formula.

Ho notato che le tensioni dell’apparecchio erano piuttosto basse e le corde piuttosto lente. Occorrono quindi pesi maggiori.

La formula può essere verificata anche così: una corda di metà lunghezza dovrebbe oscillare con la stessa altezza di una avente lunghezza doppia ma con una tensione 4 volte maggiore. In questo caso si deve considerare che una tensione 4 volte maggiore comporterà una lieve diminuzione della densità lineare r rispetto alla corda corta, e quindi un’altezza leggermente maggiore (si avranno battimenti?).