5 Pattern da riconoscere

Appignano, 27 maggio 2004

Ricerca di regolarità [1]

MODELLO QUADRATO

 Scopri la relazione tra il numero di tappi del lato e il numero dei tappi che occorrono per costruire un quadrato.

MODELLO TRIANGOLO

Con i tappi forma tanti triangoli per capire la relazione che c’è tra il numero di tappi della base e il numero totale dei tappi che servono per costruire il triangolo.

Enrico ha scoperto che aggiungendo al numero di base un numero ogni volta inferiore fino ad uno, si ottiene il numero totale dei tappi.

Dietro un’intuizione di Nicola [2], abbiamo scoperto che moltiplicando al numero di base un numero superiore di una unità e dividendo il risultato per 2 si ottiene il n° dei tappi necessari.

È stato difficile scoprire questa regola, ma essa si può applicare a tutti i numeri.

Il lavoro è stato iniziato da: Enrico, Dalila, Marianna, Mauro e completato da tutta la classe.

MODELLO CUBO

Scopri di che colore sono le facce del cubo nascosto nel barattolo.

Dai lanci già effettuati sono usciti i seguenti colori:

BIANCO: 6 volte

ROSSO: 10 volte

GIALLO: 4 volte

Ora facciamo altri lanci per capire meglio com’è il modello del cubo.

BIANCO: 58 volte

ROSSO: 27 volte;

GIALLO: 18 volte

" Secondo me il modello potrebbe essere così:

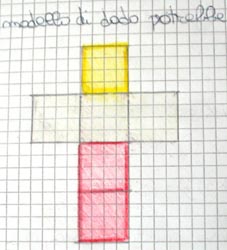
Sulla base delle uscite la maggior parte degli alunni disegna tre facce bianche, due rosse e una gialla; Dalila ha lasciato quattro facce bianche, una rossa e una gialla.

È il momento di parire il barattolo per confrontare il nostro modello con il cubo reale.

SORPRESA, il cubo è proprio come lo avevo immaginato!"

Lavoro avviato da Martina (io) Mirko, Gioele, Nico e completato insieme.

MODELLO MOLLA

Contare il numero delle oscillazioni compiute dalla molla in dieci secondi, cambiando il numero delle spire, per scoprirne la relazione.

" Abbiamo osservato che più spire si aggiungevano e più le oscillazioni diventavano lente e quindi il loro numero diminuiva.

Aiutandosi con la tabella si può fare una previsione approssimativa. Per esempio con 12 spire sii possono ottenere 12 o 13 oscillazioni.

Abbiamo verificato ottenendo 12 oscillazioni. La nostra previsione era esatta!"

Lavoro avviato da Riccardo, Maria, Jacopo, Maria Chiara e completato da tutta la classe.

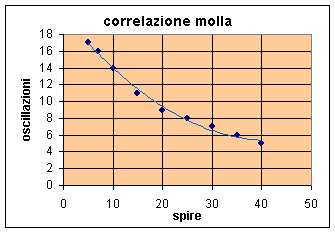
In questo caso trovare una relazione matematica tra numero di spire e numero di oscillazioni è un compito impossibile per i bambini. Il modello che consente di fare previsioni può comunque essere una semplice tabella o un grafico in un diagramma cartesiano. Dai dati della tabella dei dati sperimentali si ottiene il seguente grafico.

MODELLO CERCHIO

Misurare[3] la circonferenza e il diametro di vari oggetti circolari per capirne la relazione.

Dall’osservazione della tabella emerge questa riflessione:

-         La circonferenza misura sempre più del diametro (Nicola)

Come si può fare per trovare la relazione tra queste 2 misure?

Io ho ipotizzato che ci vuole un’operazione e Mauro ha subito intuito che questa operazione è la divisione. Quindi ora procediamo a dividere ciascuna circonferenza con il proprio diametro per scoprire se esiste un rapporto costante[4].

24   :  7 =    3,48

23   :  6,5 = 3,53

32   : 10 =   3,2

22   :   6 =   3,66

34,5: 11 =   3,14 ([5])

Giulia ha osservato che il numero intero di ogni risultato è sempre tre: il rapporto tra circonferenza e diametro è tre virgola qualcosa. La maestra ci ha detto che i matematici facendo tante, tantissime operazioni di questo genere e calcolando la media aritmetica hanno scoperto che questo rapporto è 3,14.

Lavoro avviato da Nicola, Carlotta, Simone, Giulia e completato da tutta la classe.