
Set up sperimentale che ha dimostrato la supremazia quantistica di un sistema a fotoni sul problema del Gaussian Boson Sampling. Il risultato è stato pubblicato il 3 dicembre 2020 su Science. Credit: Han-Sen Zhong et al., arXiv.
«Sarà entusiasmante vedere per la prima volta una macchina quantistica superare la più potente macchina classica nella soluzione di un problema». Così parlava a giugno del 2016 Chao-Yang Lu, ricercatore alla University of Science and Technology of China (USTC) a Hefei in un'intervista su Nature. La prestigiosa rivista britannica aveva dedicato il numero di quella settimana all'ascesa della Cina in campo scientifico e Chao-Yang Lu figurava tra i dieci ricercatori più promettenti, con l'appellativo di "mago dei quanti". Poco più di quattro anni dopo quell'intervista, la sua affermazione è diventata realtà. In un articolo pubblicato su Science la scorsa settimana Chao-Yang Lu, insieme al suo mentore Jian-Wei Pan, spesso chiamato "il padre dei quanti" dai media cinesi, e a un nutrito gruppo di collaboratori, ha dimostrato la cosiddetta "supremazia quantistica" (o "vantaggio quantistico") con un apparato costituito da fotoni. La supremazia quantistica è sostanzialmente la caratteristica di un computer quantistico di svolgere un compito in maniera clamorosamente più veloce rispetto a un computer classico.
What I said more than four years ago will appear in arXiv tomorrow pic.twitter.com/7Xwx3NddlY
— Chao-Yang Lu (@chaoyanglu) December 3, 2020
Il gruppo di Chao-Yang Lu ha mostrato con un sistema di laser, prismi, specchi e rilevatori di singoli fotoni, di saper campionare dalla distribuzione di probabilità associata a un sistema di 76 fotoni che interagiscono fra loro in circa 200 secondi (esperimento che spiegheremo più avanti nel testo). I ricercatori hanno stimato che, utilizzando il più potente supercomputer cinese TaihuLight per svolgere lo stesso compito, sarebbero necessari 2,5 miliardi di anni, un tempo centomila miliardi di volte più lungo (circa 4 ×1014 volte il tempo impiegato dal computer quantistico). Bisogna osservare che si tratta di una stima estrapolata dal tempo che è stato necessario per calcolare la distribuzione di probabilità associata a sistemi di 40 fotoni. Oltre quel limite non è possibile spingersi con nessun calcolatore classico.
«Un risultato tecnicamente notevolissimo e dal contenuto concettuale molto importante», commenta Fabio Sciarrino, professore al Dipartimento di Fisica della Sapienza, Università di Roma, che proprio su questi temi ha da poco avvitato un progetto finanziato con un ERC Advanced Grant in collaborazione con l'Istituto di Fotonica e Nanotecnologie del CNR e l'International Iberian Nanotechnology Laboratory.
Ma è la prima volta che viene dimostrata la supremazia quantistica, come auspicato dal giovane ricercatore cinese nel 2016? Difficile rispondere a questa domanda. Sicuramente è la prima volta che il problema viene affrontato con un sistema di fotoni. Esiste infatti un precedente, che risale all'ottobre del 2019, quando un gruppo di ricercatori di Google ha usato un chip quantistico chiamato Sycamore, costituito da 53 circuiti superconduttori, per risolvere in tre minuti e mezzo un problema che avrebbe richiesto diecimila anni di calcolo a un supercomputer classico. Questa conclusione è stata contestata poco tempo dopo dai ricercatori di IBM, rivale di Google nel campo della computazione quantistica, che hanno ipotizzato l'esistenza di un metodo di ottimizzazione del calcolo che permetterebbe a SUMMIT, il supercomputer ospitato dall'Oak Ridge National Laboratory in Tennessee, di farcela in due giorni e mezzo. Difficile dire, insomma, se si tratti della prima dimostrazione della supremazia quantistica in assoluto. «Credo che un risultato rafforzi l'altro più che metterne in discussione l'importanza», commenta Sciarrino.
L'inizio della computazione quantistica
Negli anni '80 il fisico Richard Feynmann, vincitore del premio Nobel nel 1985, propose l'idea che un computer quantistico, ovvero un computer in cui i bit sono sostituiti con una loro versione quantistica, chiamata qubit, potesse diventare uno strumento utile a risolvere problemi nel campo della fisica e della chimica che richiedevano la simulazione di sistemi costituiti da tante particelle interagenti tra loro in modo quantistico. I computer classici non erano adatti al compito, visto che il tempo necessario a risolvere questi problemi cresce esponenzialmente con il numero di particelle interagenti. Il vantaggio di un computer quantistico deriva dalla possibilità di codificare molta più informazione in un qubit rispetto a quanto sarebbe possibile in un bit. Se un bit può avere due soli valori, '0' oppure '1', un qubit può trovarsi in uno degli infiniti stati che si ottengono sovrapponendo '0' e '1'. Questo equivale a dire che il qubit vale '0' e '1' "contemporaneamente". Una misura del suo stato lo costringerà in uno dei due valori '0' o '1', una delle proprietà fondamentali della meccanica quantistica. Entrambi i risultati sono possibili, ma hanno probabilità diverse che dipendono dal peso che '0' e '1' hanno nello stato di sovrapposizione in cui si trova il qubit prima della misura.Ci si è chiesti poi se un sistema di calcolo basato su interazioni di tipo quantistico potesse essere utile per affrontare problemi al di fuori della fisica o della chimica. Nel 1994 il matematico americano Peter Shor inventò un algoritmo quantistico per trovare i fattori primi di un numero intero, dimostrando che questo algoritmo impiega un tempo che è polinomiale nella dimensione del numero da fattorizzare (dove per dimensione si intende il numero di bit necessari a rappresentarlo). Finora però è stato possibile implementare l'algoritmo di Shor solo su macchine con un numero molto limitato di qubit, riuscendo al massimo a scomporre in fattori primi il numero 21. Chiaramente questo non è sufficiente a dimostrare la supremazia quantistica, visto che siamo capaci di trovare a mente i due fattori primi di 21, 3 e 7. La difficoltà sta nel fatto che non appena si prova a implementare l'algoritmo di Shor con un numero maggiore di qubit per cercare di scomporre numeri più grandi, si cade vittima di diverse forme di rumore quantistico che rendono il sistema altamente instabile e inaffidabile. Il problema della ricerca dei fattori primi ha un interesse pratico molto importante, visto che uno dei protocolli di crittografia più utilizzati si basa proprio sulla difficoltà di questo calcolo per numeri molto grandi.
Cos'è la "supremazia quantistica"
La computazione quantistica sembrava dunque attraversare una stagione negativa, incapace di saper realizzare le sue applicazioni pratiche più promettenti. Un impeto positivo è arrivato nel 2011, quando John Preskill, professore alla Caltech University dove dirige l'Institute for Quantum Information and Matter, ha proposto il concetto di "supremazia quantistica", intervenendo alla venticinquesima Solvay Conference on Physics1. Come spiega lo stesso Preskill in un articolo scritto per Quantamagazine nel 2019, la "supremazia quantistica" indica il caso in cui i computer quantistici sono capaci di svolgere dei compiti che sono fuori dalla portata dei computer classici, indipendentemente dal fatto che questi siano compiti di interesse pratico (parlando più tecnicamente, per dimostrare la supremazia quantistica di un certo hardware è richiesto di provare che il tempo che gli è necessario per risolvere un problema che ha un input di dimensione n cresce come un polinomio di grado n, mentre per un computer classico cresce esponenzialmente o comunque più velocemente che un polinomio di grado n). L'intenzione di Preskill era quella di stimolare dei progressi nel campo, individuando degli obiettivi raggiungibili, piuttosto che continuare a inseguire traguardi evidentemente ancora fuori dalla portata degli esperimenti. Come vedremo, è riuscito nel suo intento.La definizione di Preskill è del tutto generale e non indica né che tipo di computer classico e quantistico dovrebbero essere confrontati, né che tipo di problema dovrebbe essere risolto. Per provare ad attaccare il problema della supremazia quantistica sono necessari quattro ingredienti fondamentali. Il primo è un problema che abbia una complessità computazionale opportuna (esponenziale per un computer classico e polinomiale per un computer quantistico). Il secondo è un algoritmo classico che funzioni da riferimento da battere e identifichi la dimensione dell'input oltre la quale il computer quantistico comincia a mostrare la sua superiorità. Il terzo ingrediente è costruire un hardware capace di funzionare sufficientemente bene oltre quella soglia. Il quarto e ultimo ingrediente, niente affatto banale, è quello di sviluppare metodi per validare il risultato ottenuto con la macchina quantistica. Infatti, visto che non esiste alcuna macchina classica in grado di riprodurre il risultato in tempi utili, è importante avere strategie per provare che l'output del computer quantistico sia corretto, pur ammettendo un certo grado di approssimazione.
La prima dimostrazione
Come abbiamo anticipato, la prima dimostrazione della supremazia quantistica è arrivata poco più di un anno fa, quando un gruppo di ricercatori di Google ha pubblicato su Nature i risultati di un esperimento di campionamento su un sistema chiamato "random quantum circuit". Il problema può essere equiparato al campionamento dalla distribuzione dei prodotti di un generatore quantistico di numeri casuali2.Il chip Sycamore utilizzato dal gruppo di Google è infatti un reticolo quadrato sui cui vertici sono posizionati dei circuiti superconduttivi, 53 in totale, che a temperature dell'ordine di -270°C si comportano come qubit. Questi sono connessi a coppie da componenti che potremmo equiparare alle porte logiche della computazione classica, e il modo in cui queste porte sono distribuite sul reticolo a ogni iterazione dell'esperimento cambia in maniera casuale.
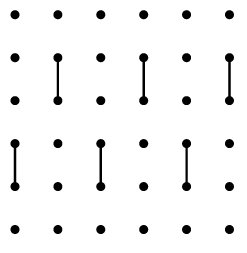
Rappresentazione schematica del chip Sycamore, utilizzato da Google nel 2019 per dimostrare la supremazia quantistica. Si tratta di un reticolo quadrato sui cui vertici sono posizionati i qubit. Alcuni di questi sono connessi da gate che possiamo immaginare come la versione quantistica delle porte logiche tipo AND e OR. La posizione delle porte sul reticolo viene cambiata in modo casuale e lo stato dei qubit sul reticolo misurato. Credit: Sergio Boxio et al., Nature Physics, 2019.
Misurando ripetutamente lo stato dei 53 qubit, i ricercatori sono stati in grado di risolvere il problema di partenza in tre minuti e mezzo, un tempo un miliardo di volte più breve di quello necessario a un supercomputer classico (diecimila anni). Poco tempo dopo IBM ha pubblicato sull'archivio di preprint arXiv un articolo in cui la conclusione del gruppo di Google veniva messa in discussione. I ricercatori di IBM sostengono infatti che esisterebbe un metodo più efficiente di calcolare la distribuzione di probabilità delle diverse configurazioni del chip partendo dai principi della meccanica quantistica e utilizzando una grande quantità di memoria. Fatto questo sarebbe sufficiente campionare da questa distribuzione per riprodurre il calcolo di Sycamore. Secondo le loro stime il supercomputer IBM impiegherebbe 2 giorni e mezzo per portare a termine l'intera procedura e non diecimila anni. Tuttavia, la validità di questa affermazione è tutta da dimostrare, visto che IBM non ha mai realizzato la strategia computazionale descritta.La seconda dimostrazione, stavolta con i fotoni
Anche se il successo di Google del 2019 nel dimostrare la supremazia quantistica fosse confermato, il risultato appena ottenuto dal gruppo della USTC di Hefei ha almeno due novità. La prima è il grado di superiorità dimostrato. Il sistema di fotoni messo a punto sarebbe in grado di eseguire il calcolo diecimila miliardi di volte più velocemente del più performante supercomputer cinese. Ci si potrebbe aspettare un colpo di scena come quello di IBM con Google dello scorso anno, cioè qualcuno che afferma di poter accelerare il calcolo sul computer classico, ma questo appare piuttosto improbabile. Scott Aaronson, professore di computer science alla University of Texas at Austin, fa notare sul suo blog che mentre l'esperimento sul chip Sycamore si confrontava con un sistema che poteva avere 9 milioni di miliardi di possibili stati (ovvero 9 × 1015, l'equivalente di 253, cioè il numero di possibili configurazioni di un sistema di 53 qubit), quello appena descritto su Science ne può avere ben 1030. La seconda novità è che è stato realizzato con un sistema di fotoni, una tecnologia del tutto differente rispetto a quella impiegata da Google.
La macchina di Galton prima e dopo il rovesciamento. Credit: Matemateca (IME/USP)/Rodrigo Tetsuo Argenton. Licenza: CC BY-SA 4.0.
Ma cosa hanno fatto i ricercatori cinesi in pratica? Possiamo immaginare un sistema simile alla macchina di Galton in cui al posto delle biglie abbiamo dei fotoni e al posto dei chiodi che deviano il percorso di caduta delle biglie abbiamo dei prismi e degli specchi che riflettono e fanno interferire tra loro i fotoni (si chiama infatti interferometro). Mentre nel caso della macchina di Galton è sufficiente contare le biglie che cadono in ciascuna colonna alla base, con i fotoni è necessario utilizzare dei misuratori in grado di rilevare l'arrivo delle particelle di luce. I ricercatori guidati da Chang-Yao Lu e Jian-Wei Pan sono stati in grado di inviare fino a 76 fotoni indistinguibili in un interferometro con 100 canali di input. Dopo aver incontrato lungo il loro percorso 300 prismi e 75 specchi, i fotoni sono stati misurati da 100 rilevatori. L'output sarà dunque una serie di stringhe '0' e '1' di lunghezza pari a cento (ci saranno degli '1' nelle posizioni corrispondenti ai rilevatori che hanno "visto" un fotone e degli '0' in corrispondenza dei rilevatori che non ne hanno "visti"). Lasciando correre il sistema per 200 secondi gli scienziati hanno osservato in media stringhe con 43 '1' e il resto '0', cioè hanno osservato in media 43 fotoni arrivare contemporaneamente all'uscita dell'interferometro. Una volta, però, hanno osservato 76 fotoni contemporaneamente. Questo vuol dire che sono riusciti a misurare uno degli output tra i 1030 possibili.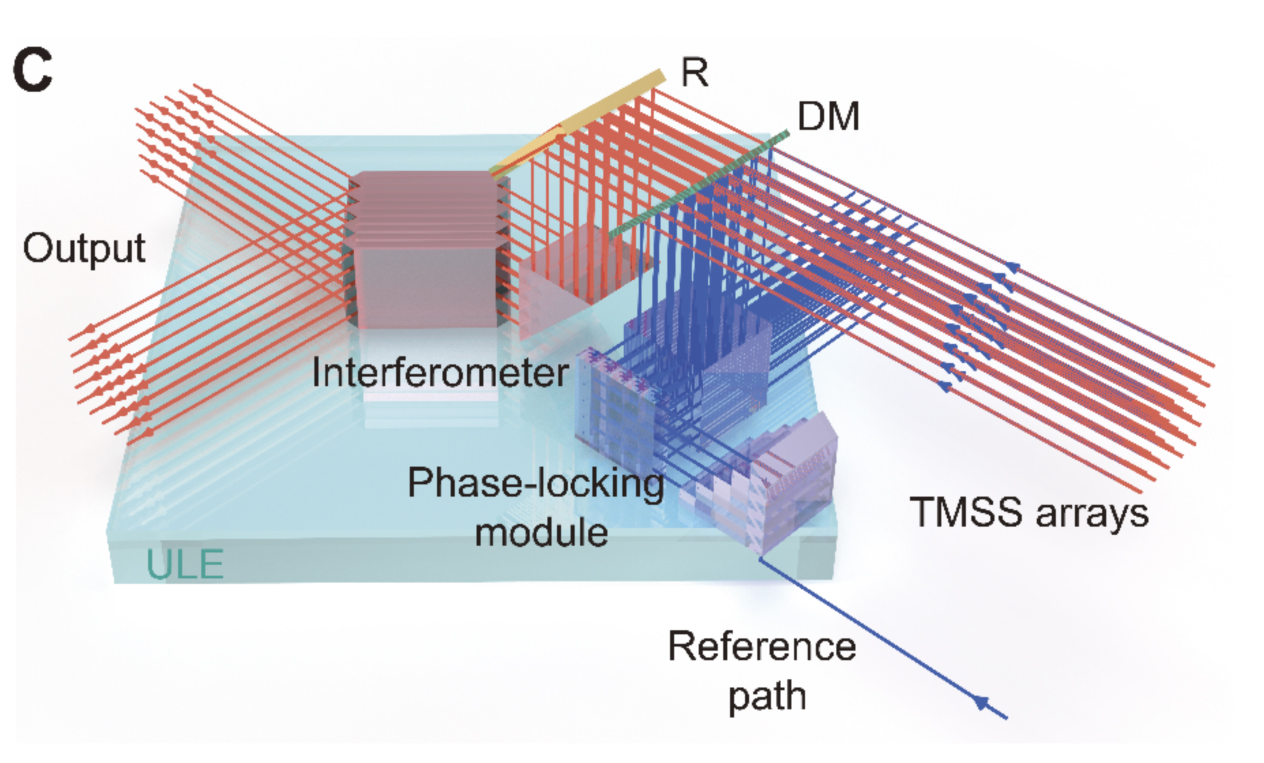
Rappresentazione schematica dell'esperimento pubblicato su Science dal gruppo della USTC a Hefei. Credit: Han-Sen Zhong et al., arXiv.
Il problema che hanno affrontato è una particolare variante del boson sampling, lo studio di un sistema di bosoni (una delle due categorie di stati quantistici a cui appartengono anche i fotoni) che interferiscono fra loro tramite prismi e specchi. Nel 2011 Scott Aaronson e Alex Arkhipov hanno dimostrato non solo che calcolare la probabilità di osservare una certa sequenza di '0' e '1' con i rilevatori di fotoni posti alla fine del percorso di interferenza è un problema incredibilmente difficile per un computer classico, ma anche che campionare da quella distribuzione è un problema altrettanto difficile. Parlando più tecnicamente, i due ricercatori hanno provato, usando tecniche matematiche molto sofisticate, che è estremamente poco plausibile che il problema sia polinomiale nella dimensione dell'input (il numero di fotoni che interagiscono) per un computer classico. La loro dimostrazione vale per un qualunque algoritmo classico e dunque è estremamente generale.Una volta formulato il problema dal punto di vista teorico, il lavoro si è spostato nel campo sperimentale. Era infatti necessario mettere a punto un sistema con un numero di fotoni sufficientemente grande per poter raggiungere il punto oltre il quale si manifesta in maniera eclatante il vantaggio di una macchina quantistica sulla più potente macchina classica. Come spesso succede nella scienza ci si è arrivati per passi intermedi. Il primo di questi passi è stato compiuto alla fine del 2012 contemporaneamente da quattro gruppi di ricercatori, tra cui quello guidato da Sciarrino, utilizzando tre fotoni per dimostrare il funzionamento del protocollo proposto da Aaronson e Arkhipov. Il calcolo della distribuzione di probabilità di tre fotoni che interferiscono è facile da ottenere anche con un computer classico, ma i risultati dei quattro gruppi hanno mostrato che l'esperimento proposto era in principio fattibile con un hardware quantistico. Lo scorso anno il gruppo di Chao-Yang Lu e Jian-Wei Pan ha fatto un ulteriore passo avanti, riuscendo a misurare l'output di un esperimento in cui 14 fotoni interferivano attraverso un sistema di specchi e prismi. Un risultato per nulla scontato, ma purtroppo ancora insufficiente a dimostrare il vantaggio quantistico. Sono bastati dodici mesi di lavoro per battere il proprio risultato e Chao-Yang Lu promette di non fermarsi qui e di aumentare il numero di fotoni fino a oltre 80 nell'arco di due mesi e di dare dimostrazione di un utilizzo del loro sistema per risolvere un problema "pratico" entro il 2021. Esistono infatti prove che la variante del boson sampling realizzata dal gruppo cinese possa essere d'aiuto nel campo della chimica quantistica e della teoria dei grafi.
don't guess. here is the goal. in 2 months, go to 80+ photons and 144 modes. by the end of 2021, demo a practical use.
— Chao-Yang Lu (@chaoyanglu) December 5, 2020
Le reazioni degli esperti
I commenti degli esperti del settore sono stati per lo più entusiasti. Christine Silberhorn, professoressa di ottica quantistica alla Paderborn University in Germania, ha definito l'esperimento una "pietra miliare" in una intervista per il Financial Times. Dello stesso avviso è Ian Walmsley, professore all'Imperial College, che, intervistato da Nature, aggiunge «Dato che l'esperimento riproduce molto fedelmente lo schema proposto da Aaronson e Arkhipov, è improbabile che si possa formulare un algoritmo classico più efficiente».Leggermente meno entusiasti i commenti di John Martinis, a capo del gruppo che ha ottenuto la prima dimostrazione della supremazia quantistica nel 2019 sul chip Sycamore di Google e che oggi è professore alla University of New South Wales a Sidney. Intervenendo durante un summit sull'innovazione in Australia Martinis ha dichiarato: «Nonostante siano riusciti a far funzionare le cose, e questo è di per sé interessante, le loro conclusioni sulla complessità computazionale del problema che risolvono non sono del tutto giustificate. La giuria si è riunita e deve deliberare (“the jury is still out”). Questo è quello che accade nella scienza». Una delle questioni che secondo Martinis è ancora aperta è se la macchina utilizzata nell'esperimento di Lu e Pan sia programmabile e dunque capace di svolgere diversi compiti oltre quello considerato. Se così non fosse il loro risultato sarebbe molto meno significativo secondo Martinis.
«La programmabilità dell'apparato realizzato da Chang-Yao Lu e collaboratori è limitata per ora, e questo è dovuto al fatto che hanno dovuto scegliere una configurazione che minimizzasse il più possibile le perdite e che gli permetterà di raggiungere rapidamente dimensioni ancora maggiori», spiega Sciarrino. «Il passo successivo è capire come sfruttare pienamente le conseguenze tecnologiche del loro risultato» continua, «ma questo di certo giustifica e incoraggia gli enormi investimenti che sono stati fatti in questo settore negli ultimi anni».
L'alba di una nuova epoca
La dimostrazione della supremazia quantistica segna l'alba di una nuova era tecnologica, quella che Preskill definisce la noisy intermediate-scale quantum technology (NISQ). Si tratta dell'era in cui si svilupperanno computer quantistici di taglia intermedia, cioè con un numero limitato di qubit, e su cui si avrà un controllo limitato, per questo noisy. Queste macchine sono ancora molto lontane dai computer quantistici capaci di rivoluzionare la nostra società. Nonostante ciò i computer NISQ potrebbero essere utili a realizzare simulazioni fisiche più accurate e magari, immagina Preskill, «giocandoci potremo capire di più su cosa sono capaci di fare». In un articolo pubblicato sull'Economist a settembre si faceva notare che esistono già investimenti consistenti in questo settore da parte dei fondi di venture capital.Chi sta investendo più massicciamente sulla computazione e l'informazione quantistica sono però i governi, che negli ultimi anni hanno riversato grandi quantità di fondi in questo campo, dando inizio a programmi di ricerca coordinati a livello nazionale e internazionale. Il Regno Unito ha avviato nel 2014 il National Quantum Technology Programme finanziandolo con 1 miliardo di sterline; la Russia ha adottato una roadmap dedicata alle tecnologie quantistiche all'interno del programma nazionale per l'economia digitale, che riceverà fondi per un totale di 1 miliardo di euro; alla fine del 2018 il congresso USA ha approvato il Quantum Initiative Act, con una dotazione finanziaria di 1,2 miliardi di dollari; la Commissione Europea ha avviato nel 2018 un programma decennale chiamato Quantum Flagship Initiative con un finanziamento di un miliardo di euro, seguendo lo stesso schema della Graphene Flagship Initiative e dello Human Brain Project. Infine la Cina, che sembra essere particolarmente aggressiva in questo settore. Nel decennio 2009-2019 ha speso quasi un miliardo di dollari nel campo dell'informazione quantistica, realizzando, tra le altre cose, il lancio del satellite Micius nel 2016. Inoltre dovrebbe essere giunta al termine la costruzione del National laboratory for quantum information sciences costato 10 miliardi di dollari. Le tecnologie quantistiche sembrano, insomma, rappresentare uno dei settori in cui la competizione tra le due super potenze, Cina e Stati Uniti, è particolarmente agguerrita, soprattutto considerando l'impatto che queste potrebbero avere in campo militare. Per avere un'idea di come proceda questa competizione, basti pensare che nel 2018 in Cina sono stati depositati 517 brevetti nel campo della comunicazione quantistica e della crittografia, mentre negli Stati Uniti "solo" 117. Insomma: la Cina sembra avere tutta l'intenzione di guidare la transizione verso la nuova era della computazione, assumendo così il ruolo che gli Stati Uniti hanno avuto all'alba della prima rivoluzione informatica.
Note
1 Oggi all'espressione "supremazia quantistica", molti preferiscono quella di "vantaggio quantistico". Il termine "supremazia" rischia infatti di essere associato alla "supremazia bianca" evocando violenza, neocolonialismo e razzismo.
2 Qui un video che illustra il lavoro del 2019 dei ricercatori di Google, realizzato dalla giornalista di Nature Elizabeth Gibney.
Per ricevere questo contenuto in anteprima ogni settimana insieme a sei consigli di lettura iscriviti alla newsletter di Scienza in rete curata da Chiara Sabelli (ecco il link per l'iscrizione). Trovi qui il testo completo di questa settimana.
Buona lettura, e buon fine settimana!



