In matematica e in economia, il problema del trasporto ottimale consiste nello studio di come trasferire una distribuzione di massa da un luogo a un altro ‘’in maniera ottimale”. Questo problema fu formalizzato per la prima volta nel trattato di Gaspard Monge del 1781, Mémoire sur la Théorie des Déblais et des Remblais, (ossia Trattato sulla teoria degli scavi e terrapieni). Nel caso particolare studiato da Monge, ci si domandava quale fosse la maniera ottimale di spostare della terra per costruire delle fortificazioni, supponendo che il “costo di trasporto” sia proporzionale alla distanza.
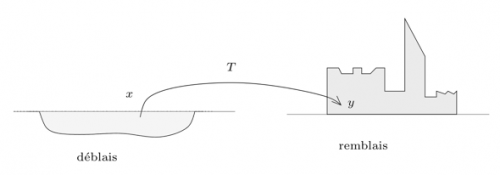
Un problema assolutamente non banale, da un punto di vista matematico, è sapere se un tale trasporto ottimale esista (e, in tal caso, se sia unico o meno).
Un primo importante progresso della teoria si deve al matematico e economista russo Leonid-Kantorovich, il quale negli anni ’40 del secolo scorso scrisse diversi trattati sulla materia che gli valsero, nel 1975, il premio Nobel per l’economia. Da un punto di vista matematico, il merito principale di Kantorovich è stato di dare una nuova formulazione del problema che permettesse alla massa che parte da un punto fissato di poter essere ‘’divisa’’ e inviata su più punti.
Questo "splitting" della massa è assolutamente naturale (e, anzi, desiderabile) se si pensa al problema seguente: supponiamo di avere un numero N di miniere di ferro, da ciascuna delle quali si estrae una certa quantità ai di ferro (i=1,…,N), e di avere M industrie, ciascuna delle quali richiede una quantita’ bj di ferro come materia prima (j=1,…,M). Supponendo che a1+…+aN=b1+…+bM (ossia produzione=domanda), risulta naturale (e in molti casi inevitabile) che una stessa miniera possa rifornire diverse fabbriche allo stesso tempo (ovviamente, fornendo quantità diverse a ognuna delle fabbliche). Quindi, in questo caso, non esiste nessun trasporto ottimale, dato che non si può associare a ciascuna miniera una sola fabbrica in maniera univoca.
Come conseguenza di questi lavori, il problema del transporto ottimale è attualmente anche chiamato ‘’problema di Monge-Kantorovich”.
Per quanto i lavori di Kantorovich avessero dato un grande impulso alla teoria del transporto ottimale in ambito economico, in matematica mancava ancora una vera teoria e il problema non aveva ancora riscosso un grande interesse.
Il boom del trasporto ottimale nella communità dell’analisi matematica si deve certamente ai lavori di Yann Brenier alla fine degli anni ’80. In quel periodo Brenier stava studiando problemi legati alla meccanica dei fluidi (più precisamente, le equazioni di Eulero per i fluidi incomprimibili) e si trovò di fronte a questioni che lo portarono (in maniera piuttosto inaspettata) al problema di Monge-Kantorovich, ma non con un costo di trasporto proporzionale alla distanza, bensì al quadrato della distanza (una sorta di “energia cinetica”). Brenier dimostrò in questo caso esistenza e unicità di un trasporto ottimale (l’esistenza di un trasporto nel caso costo=distanza era in quel momento ancora un problema aperto e fu risolto solamente alla fine degli anni ’90 grazie al contributo di vari matematici).
Il lavoro di Brenier fu importante non solo per il risultato in sè (ossia l’esistenza e unicità di un trasporto ottimale quando il costo è proporzionale alla distanza al quadrato), ma soprattutto per aver mostrato una connessione con problemi derivanti dalla meccanica dei fluidi. Questa è sicuramente una delle proprietà che sono alla base del successo del trasporto ottimale nella comunità dei matematici: il fatto di avere legami con altri settori della matematica. Infatti, il caso di Brenier fu il primo ma tutt’altro che l’ultimo: durante la metà degli anni ’90 del secolo scorso Robert McCann, che stava studiando la meccanica dei gas, mostrò che il trasporto ottimale si poteva applicare anche in questo contesto: l’idea di fondo è che, una volta noto come trasportare una distribuzione di massa (o gas) da una configurazione a un’altra, si può vedere questo come un processo continuo: se il trasporto ottimale invia un punto x su un punto y, allora si considera il segmento che congiunge x a y e si decide di muovere il punto x a velocità costante lungo questo segmento in modo che al tempo 0 si trovi in x e al tempo 1 si trovi in y. Così facendo, per ogni istante di tempo t compreso tra 0 e 1(0<t<1), il gas assume una famiglia di configurazioni “intermedie” che interpolano in maniera naturale tra lo stato iniziale e quello finale.
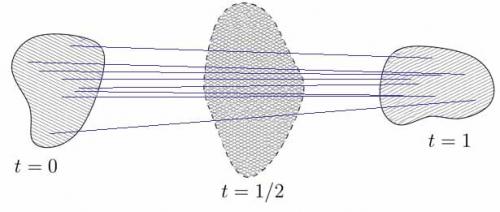
McCann chiamò questa maniera di passare da una configurazione all’altra “displacement interpolation”. Tra le varie applicazioni, questo tipo di interpolazione permette di dimostrare importanti disuguaglianze geometriche (tra cui, per esempio, le disuguaglianza isoperimetriche).
La lista delle applicazioni del trasporto ottimale non finisce però qui: negli ultimi 10 anni sono stati scoperti legami con la teoria delle equazioni alle derivate parziali, la geometria differenziale, etc.
Questo continuo emergere di legami con altri settori della matematica ha reso, e continua a rendere, il trasporto ottimale un argomento affascinante e estremamente attivo della matematica dei nostri giorni.



