L’indice di riproduzione netta del contagio R(t)1 è un parametro importante per monitorare l’evoluzione di un’epidemia, e la COVID-19 non fa eccezione. Da quasi un anno è entrato nel nostro linguaggio quotidiano e, con la seconda ondata arrivata in Europa e in Italia dopo l’estate, è stato scelto come strumento di governo dell’epidemia. A partire dal 3 novembre le misure per contenere il contagio sono state differenziate tra le diverse regioni anche in base al valore di R(t). Questo sistema è stato aggiornato il 14 gennaio con un nuovo decreto del Presidente del Consiglio dei Ministri, che ha dato maggior peso al livello di incidenza settimanale del contagio nell’assegnazione dei colori (l’incidenza è il numero di nuovi casi di infezione registrati nell’arco di una settimana in una certa regione in percentuale sulla popolazione).
R(t) è il numero medio di infezioni che una persona positiva causa nel suo periodo di contagiosità. Se R(t) è sopra 1 allora il numero di infezioni è destinato ad aumentare, se è sotto 1 invece il numero di infezioni di domani sarà più piccolo di quello di oggi e lo stesso avverrà il giorno successivo. R(t) è il risultato della biologia del virus e dei nostri comportamenti. Per il SARS-CoV-2 l’indice di riproduzione di base, cioè quello dovuto alla sola biologia senza misure di contenimento è intorno a 3 (almeno per la variante attualmente dominante in Italia). È quindi necessario mantenere le distanze, limitare i contatti e indossare le mascherine per far scendere questo numero sotto 1. Per stimarlo esistono diversi metodi. Finora le istituzioni italiane, come molte altre in Europa, hanno usato il metodo proposto e validato dal gruppo di epidemiologi dell’Imperial College di Londra2. In Italia è la Fondazione Bruno Kessler a essere responsabile di questa stima su incarico dell’Istituto Superiore di Sanità (qui una spiegazione dettagliata). L’R(t) stimato dalla Fondazione Bruno Kessler viene pubblicato nei report settimanali del monitoraggio regionale da ormai 36 settimane (l’ultimo è pubblicato qui). Il metodo parte dalla curva dei nuovi casi sintomatici organizzati secondo la data di inizio dei sintomi relativa a ciascuna regione. Qui sotto mostriamo la curva a livello nazionale per il periodo 1 agosto 2020 - 13 gennaio 2021 (i dati sono stati ottenuti dal sito web dell’Istituto Superiore di Sanità il 23 gennaio 2021).
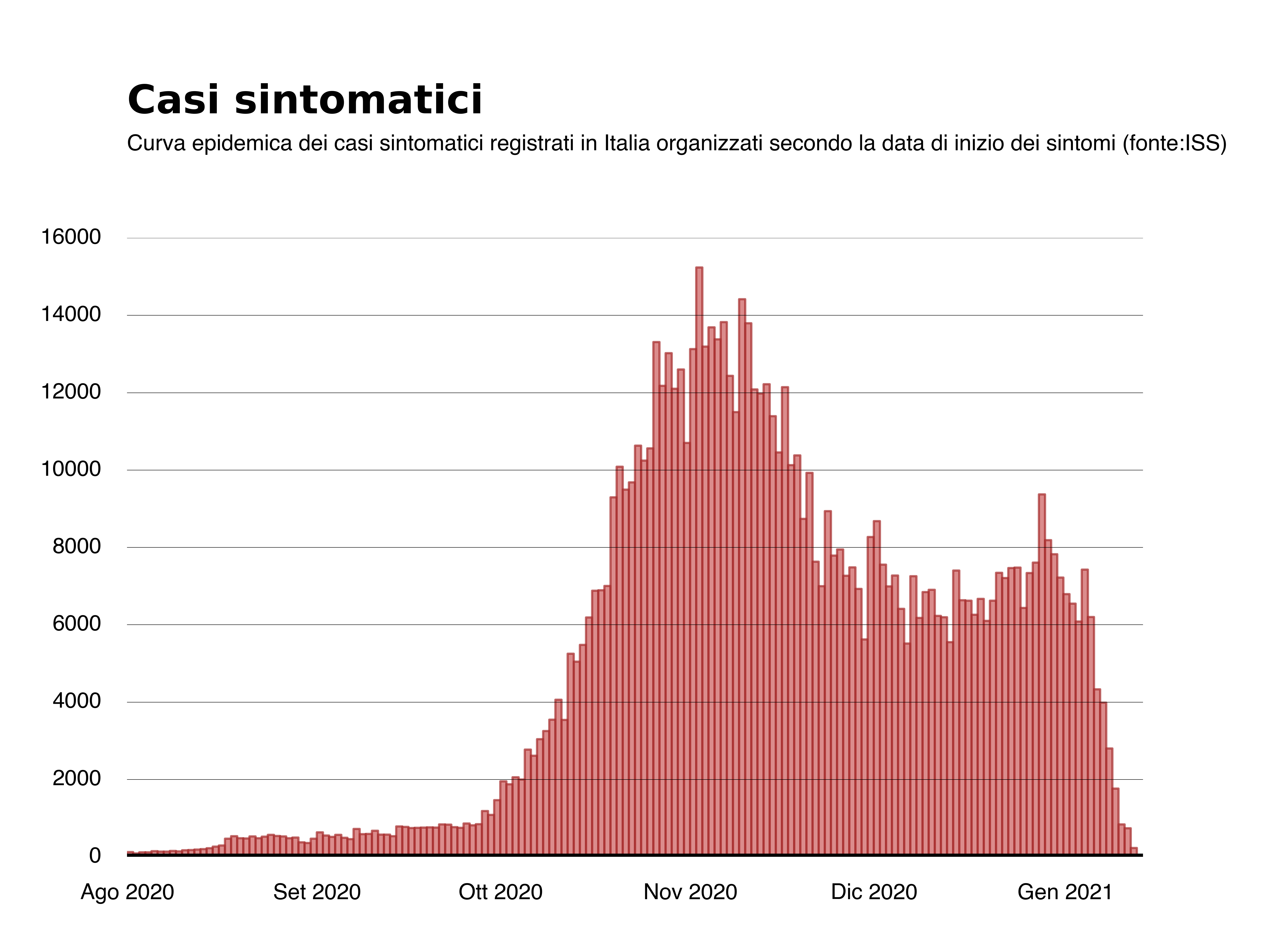
Tramite tecniche di inferenza bayesiana viene calcola la distribuzione di probabilità del valore di R(t). Più precisamente si calcola la media e l’intervallo di credibilità al 95% di questa distribuzione. Da questi parametri si ottiene un intervallo di valori probabili per R(t).
Ad esempio, nel rapporto settimanale pubblicato il 13 gennaio e relativo alla settimana tra il 4 e il 10 gennaio, per la Lombardia l’intervallo di credibilità di R(t) era stimato essere [1,38:1,43]. Questo equivale a dire che in Lombardia l’R(t) aveva un valore che cadeva da qualche parte tra il limite inferiore di 1,38 e il limite superiore di 1,43. Visto che il limite inferiore di questo intervallo di credibilità era maggiore della soglia di 1,25 e il limite superiore era minore della soglia di 1,5, la Lombardia è stata classificata in uno scenario 3 (in una scala da 1 a 4, definita in questo documento). Inoltre l’incidenza settimanale era pari a 133,3 persone ogni 100 000 abitanti, superiore alla soglia di 50 ogni 100 000 abitanti stabilita nel decreto del 14 gennaio. Trovandosi in uno scenario 3 e avendo incidenza superiore a 50 ogni 100 000 abitanti, insieme al fatto che il rischio era valutato come alto (principalmente a causa dell’elevato grado di saturazione delle terapie intensive) la regione è finita in zona rossa dal 17 gennaio. L’amministrazione della regione Lombardia ha contestato questa decisione, sostenendo che ci fosse un errore nella stima di R(t). Il valore “corretto” sarebbe stato inferiore e avrebbe portato la regione in uno scenario di tipo 2 e non 3. Come conseguenza la Regione si sarebbe trovata in zona arancione. È notizia di ieri che R(t) sia stato effettivamente sovrastimato, ma non per responsabilità della Fondazione Bruno Kessler, bensì per via di un errore nei dati trasmessi dalla regione al Ministero proprio riguardo la curva dei casi sintomatici (come ha fatto notare Andrea Capocci su Twitter, partendo da questo comunicato stampa dell'ISS). Dunque la Lombardia è stata ingiustamente classificata zona rossa e da oggi torna in zona arancione.
La vicenda della Lombardia mostra come la stima di R(t) possa essere sporcata da errori nella trasmissione dei dati sulla curva dei sintomatici da parte delle Regioni. Oltre a questa fragilità, però, la curva soffre di alcuni difetti “metodologici”. In particolare, il numero di nuovi casi giornalieri registrati ha un andamento che dipende dal numero dei tamponi fatti e dunque risulta in generale sottostimato rispetto al numero reale di nuovi casi. Ciò che però è più rilevante per la stima di R(t) è l’andamento di questa curva, cioè il modo in cui aumenta e diminuisce. Se per esempio in un certo periodo di tempo il numero di tamponi fatti al giorno tende ad aumentare, il numero di nuove infezioni registrate tenderà a crescere più rapidamente rispetto alla crescita del numero reale di nuovi casi e questo porterà a una sovrastima del valore di R(t). Al contrario, se in un certo periodo di tempo il numero di tamponi tende a ridursi progressivamente, avremo una decrescita del numero di nuovi casi che non fotografa l’andamento reale della diffusione della malattia.
Un metodo alternativo, e in qualche misura più semplice e intuitivo, per la stima di R(t) è stato proposto da Roberto Battiston in questo articolo pubblicato su Scienza in rete. Battiston propone di partire dalla curva degli infetti attivi (cioè il numero totale delle persone infette giorno dopo giorno e che da qui in poi chiameremo semplicemente curva degli infetti) e calcolare R(t) utilizzando il modello SIR3, un modello matematico che descrive tramite equazioni differenziali l’evoluzione temporale congiunta di tre popolazioni: i suscettibili, gli infetti e i rimossi (guariti+morti). Tuttavia, anche la curva degli infetti ha dei limiti. Nel grafico qui sotto la mostriamo in blu, insieme alla curva dei nuovi casi registrati in rosso (stavolta mostriamo il totale delle nuove infezioni registrate, sintomatiche e non, ogni giorno secondo la data di diagnosi). I dati sono quelli pubblicati dalla Protezione Civile e si riferiscono all’epidemia in Italia dal 1 giugno 2020 al 19 gennaio 2021.
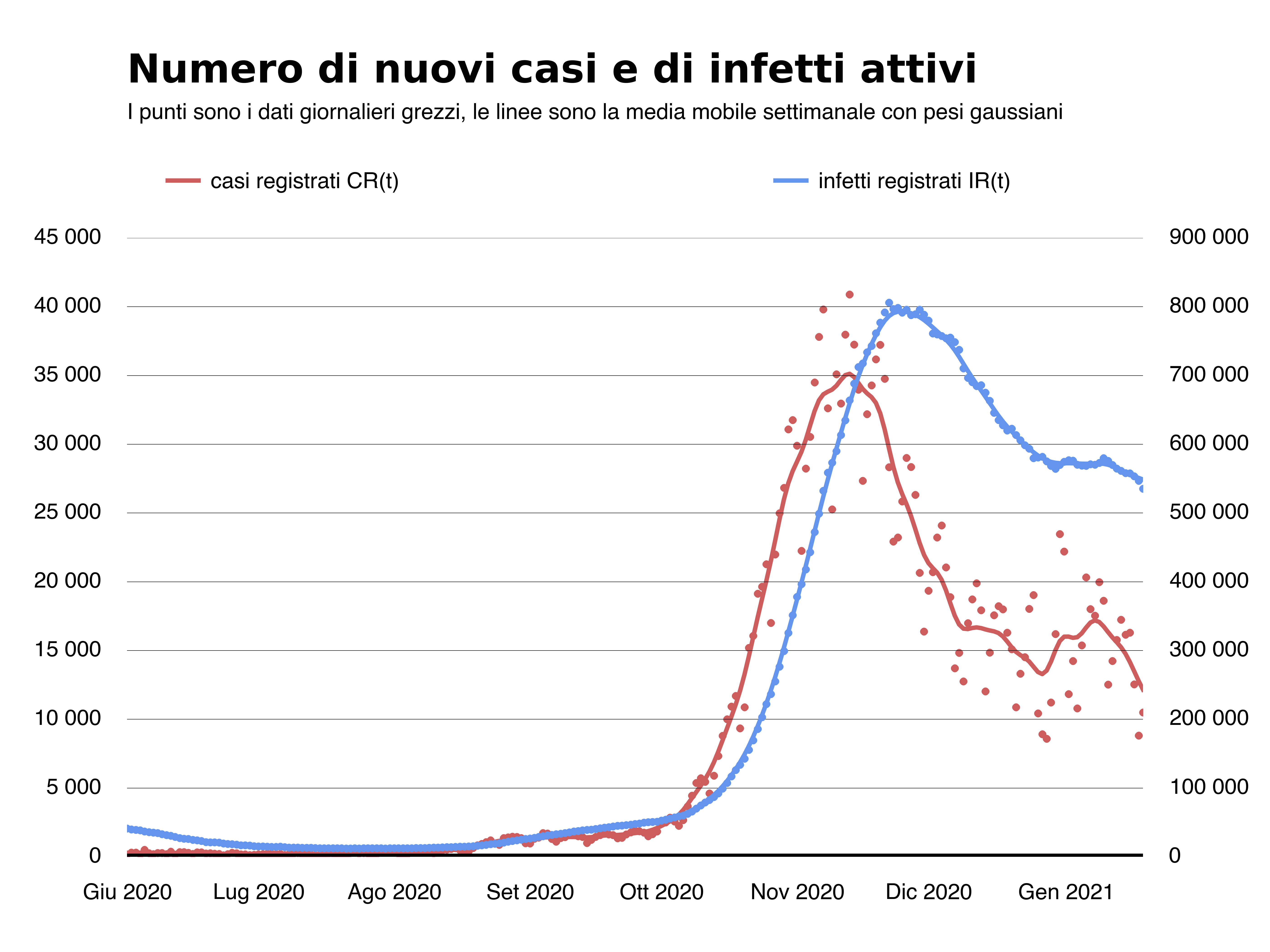
Nelle fasi di picco, fra i casi registrati ci sarà un eccesso di casi gravi, che necessitano di un maggiore tempo di ospedalizzazione o isolamento e il cui decorso è in media più lungo, sia che porti alla guarigione che alla morte. È ragionevole dunque aspettarsi che il tasso di decrescita della curva degli infetti sia in generale più lento rispetto a quello degli infetti reali. La curva degli infetti risulterà quindi eccessivamente ritardata rispetto a quella dei nuovi casi registrati, come in effetti si vede bene nella figura sopra, dove notiamo una differenza tra 15 e 20 giorni tra i picchi della curva dei nuovi casi e quella degli infetti mentre sulla base della stima del tempo medio dell’infezione4 ci aspetteremmo un ritardo non superiore a 10 giorni. Inoltre, sempre per lo stesso motivo, notiamo una velocità di discesa molto bassa della curva degli infetti: questo sia perché i malati gravi per COVID-19 necessitano di tempi lunghi sia per guarire che per morire, sia perché è necessario aspettare il tempo di isolamento e quello dovuto al tampone che accerta la guarigione.
Una possibilità è quella di ricorrere alle curve dei tassi di positività rispetto ai tamponi o ai casi testati5. Nell’immagine sotto confrontiamo queste due curve con quella dei nuovi casi registrati.
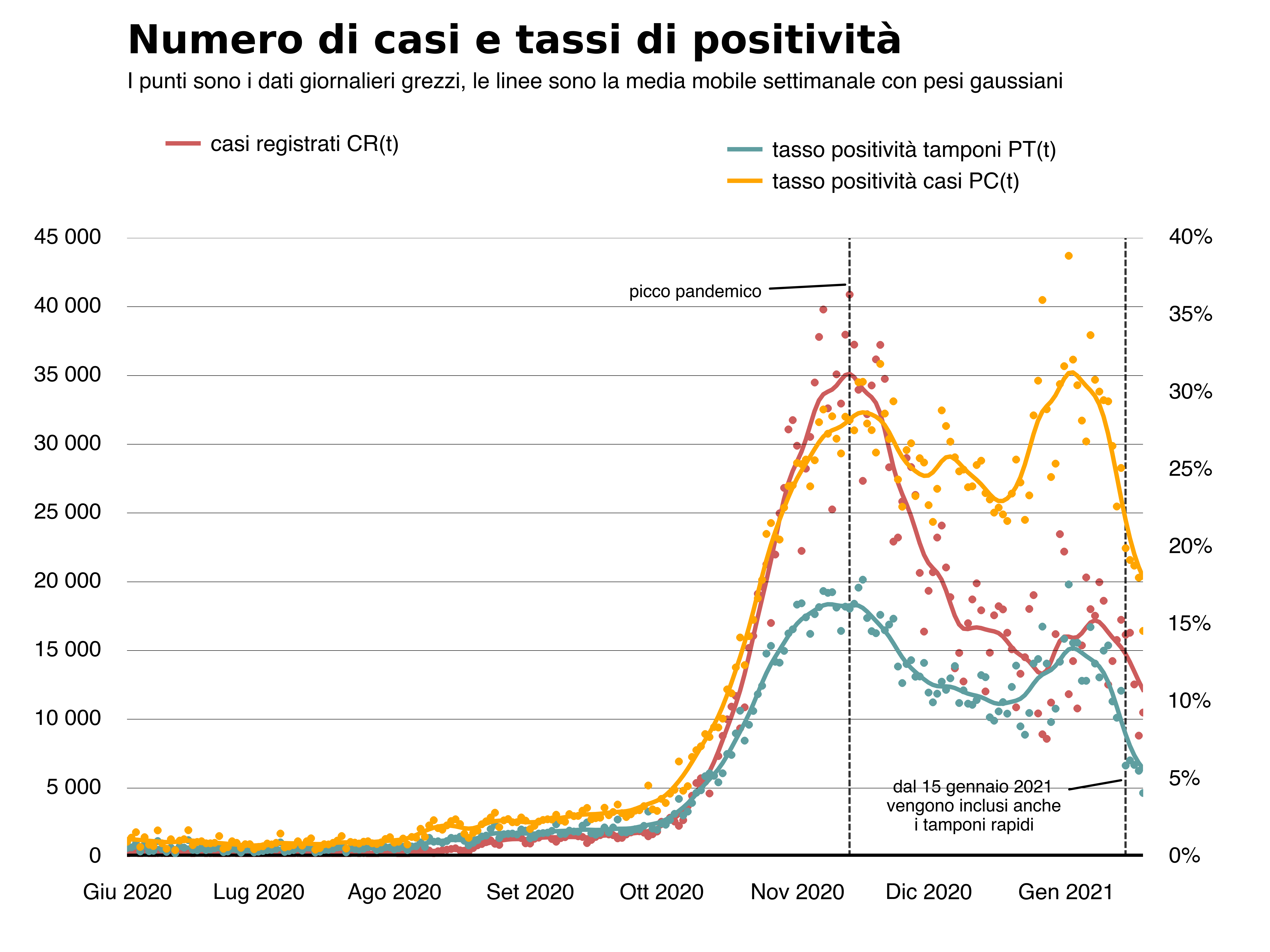
Dopo il picco pandemico, notiamo una diminuzione più veloce dei nuovi casi registrati rispetto al tasso di positività dei tamponi e del numero di casi testati al giorno, dovuta evidentemente alla diminuzione del numero di tamponi effettuati. Inoltre, sempre dopo il picco si osserva anche che il tasso di positività rispetto ai casi testati appare più livellato rispetto a quello relativo ai tamponi. Questa differenza è dovuta al fatto che dall’inizio di novembre il rapporto tra numero di tamponi effettuati e numero di casi testati è andato aumentando e ciò ha determinato una diminuzione più veloce del tasso di positività dei tamponi rispetto a quello dei casi testati. Effettivamente è quello che è accaduto, come si vede bene nella figura qui sotto in cui mostriamo l’andamento del rapporto tra numero di tamponi effettuati e numero di casi testati.
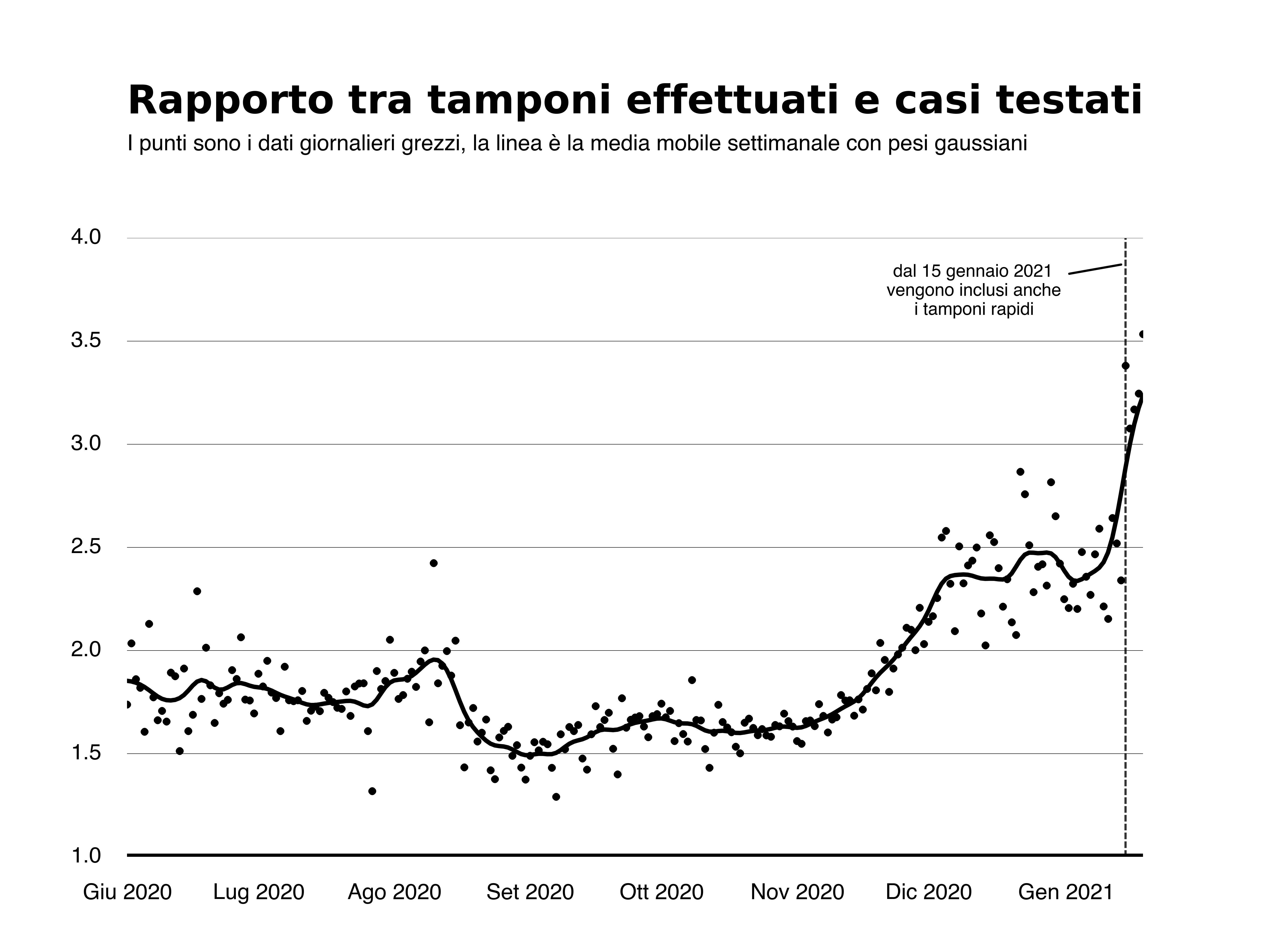
Si vede l’aumento a partire da novembre e poi una crescita brusca dal 15 gennaio 2021 in poi. Questo è dovuto al fatto che da quella data vengono considerati anche i tamponi rapidi oltre a quelli molecolari nel totale dei tamponi effettuati. Questo brusco aumento si riflette in una drastica caduta del tasso di positività rispetto ai tamponi.
Il cambio di strategia nel conteggio dei tamponi intercorso il 15 gennaio compromette dunque l’affidabilità delle curve dei tassi di positività. Una possibilità potrebbe essere quella di utilizzare i dati relativi ai soli tamponi molecolari, che la Protezione Civile rende pubblici, ma esiste un altro problema metodologico ben spiegato in quest’articolo di Cesare Cislaghi su Scienza in rete. In sostanza, perché le curve dei tassi di positività siano affidabili nel fotografare la diffusione del virus, il campione di persone che ricevono un tampone dovrebbe essere rappresentativo della popolazione (una proposta di istituire un sistema di monitoraggio simile è stata avanzata dagli statistici già direttori dell’ISTAT Alleva e Zuliani e documentata qui su Scienza in rete). Al contrario, il campione è costituito da diversi gruppi (persone che si recano in ospedale per patologie non collegate all’infezione, contatti stretti di positivi, chi ha ricevuto un risultato positivo da un test rapido e ne vuole confermare l’esito, persone che svolgono lavori a rischio) in proporzioni non controllate e variabili.
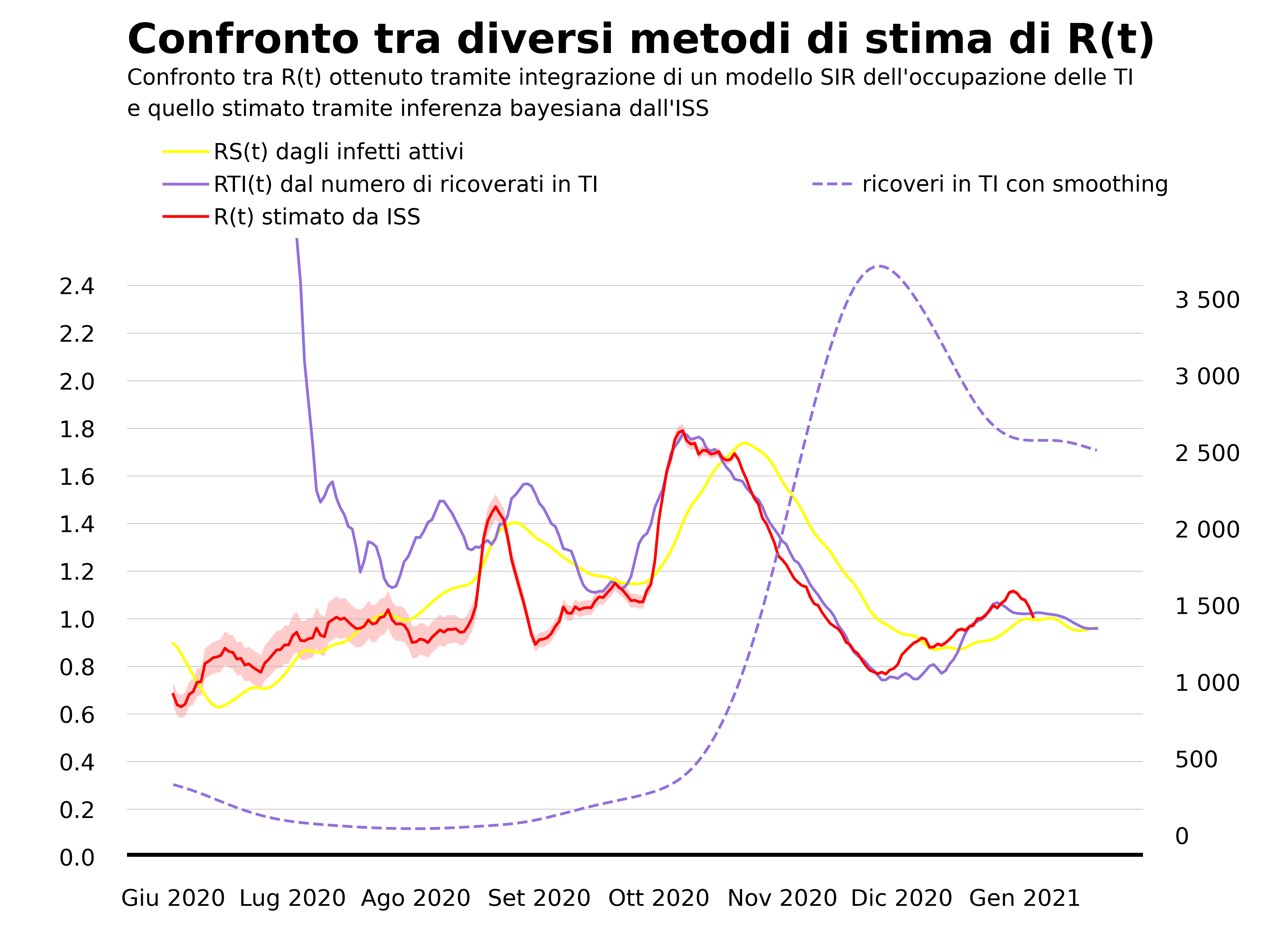
La nostra proposta è dunque quella di partire dall’unico dato che sembra restare affidabile, ovvero il numero di letti occupati da pazienti con COVID-19 nei reparti di terapia intensiva. Anche in questo caso si può costruire un modello tipo SIR che collega l’evoluzione nel tempo di questo numero col numero degli infetti e da questo ottenere una stima di R(t) (descriviamo il modello nell’appendice). Il risultato è quello che riportiamo qui sotto, dove lo confrontiamo con la stima proposta da Roberto Battiston che parte dalla curva degli infetti e con quella dell’Istituto Superiore di Sanità6.
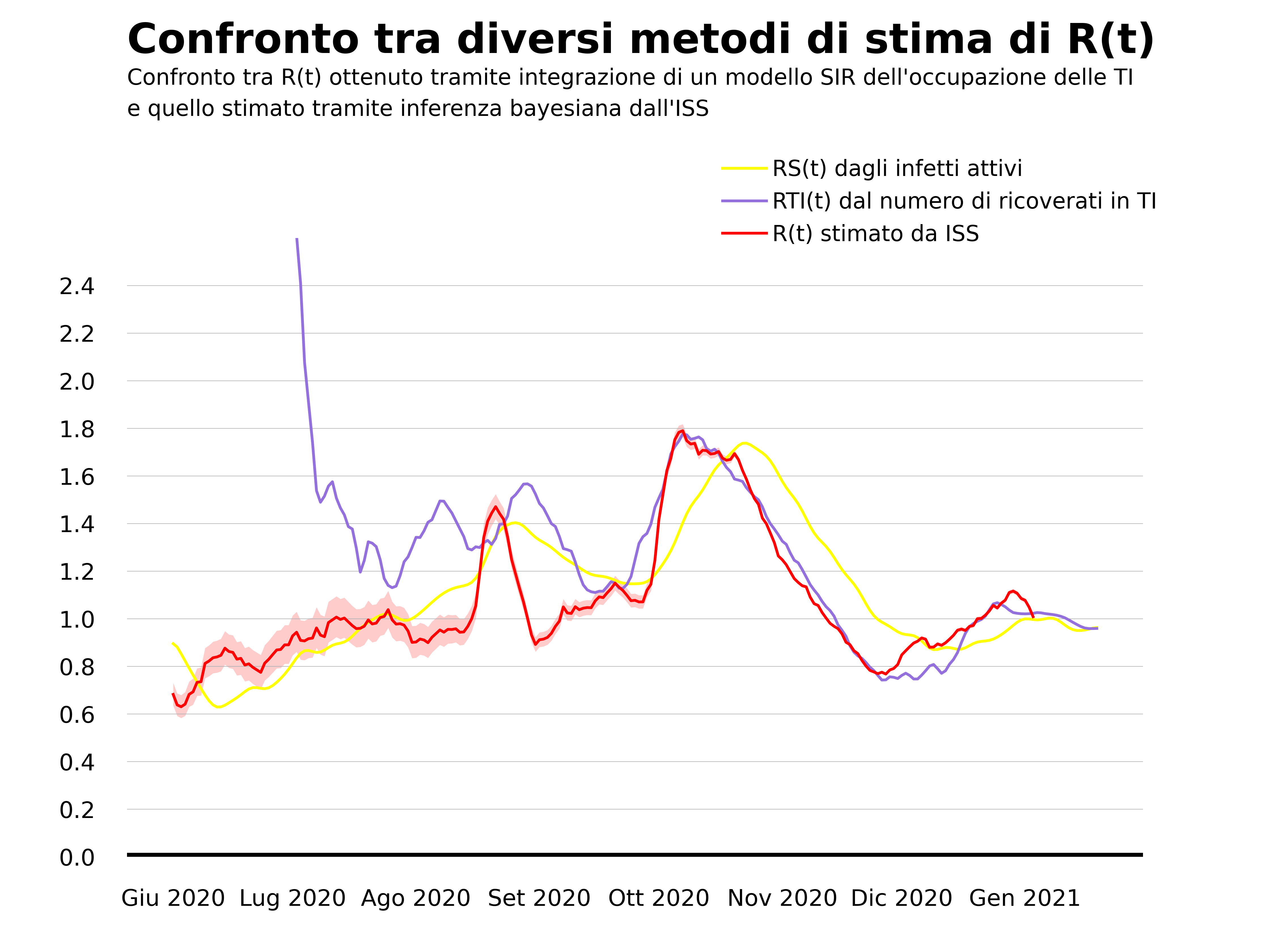
La prima osservazione è che nel periodo estivo la stima di R(t) basata sul numero di persone con COVID-19 ricoverate in terapia intensiva (linea viola), che per brevità indichiamo con RTI(t), non è affidabile. Questo è dovuto al fatto che il numero di infetti ricoverati in terapia intensiva in quel periodo era piccolo e variazioni di poche unità generano variazioni di grande entità in RTI(t). Per questo nel grafico abbiamo mostrato la stima di RTI(t) a partire dal 1 luglio 2020. La seconda osservazione riguarda il periodo che va da fine ottobre in poi. Si vede che la stima di R(t) ottenuta dalla curva degli infetti (linea gialla) cresce con ritardo rispetto sia alla stima dell’ISS (linea rossa) che a RTI(t). Al contrario RTI(t) raggiunge il picco sostanzialmente insieme all’R(t) stimato dall’ISS. Lo stesso discorso vale per la discesa. L’R(t) calcolato dalla curva degli infetti decresce con ritardo, per i motivi che abbiamo spiegato prima, mentre RTI(t) risulta in buon accordo con la stima dell’ISS anche nella fase decrescente dell’epidemia.
In conclusione, la nostra proposta ha il pregio di non dipendere dai dati che le Regioni inviano all’Istituto Superiore di Sanità (la curva dei casi sintomatici organizzata secondo la data di inizio dei sintomi) ma può essere ricavata a partire dai dati comunicati giornalmente dalla Protezione Civile. Inoltre la nostra stima appare più affidabile rispetto a quella che si basa sulla curva degli infetti. Tuttavia, il nostro metodo ha due limiti. Il primo è di non essere affidabile in fasi dell’epidemia in cui c’è un numero ridotto di persone ricoverate in terapia intensiva o in regioni che anche nei picchi di contagio hanno pochi ricoveri in terapia intensiva (si potrebbe pensare, per queste regioni, di modificare la nostra proposta considerando la curva dei ricoveri nei reparti ordinari). Il secondo è che non permette di stimare il grado di incertezza che grava sul valore di R(t), al contrario di quanto accade con il metodo utilizzato dall’ISS che si basa su una formulazione più solida del problema di inferenza. Quest’ultimo non è un limite trascurabile, visto che in alcune fasi dell’epidemia l’intervallo di credibilità di R(t) può essere anche molto ampio. Come ha discusso il sociologo della scienza Warren Pearce in questo articolo pubblicato pochi mesi fa sulla rivista Human and Social Sciences Communications considerando l’esperienza del gruppo di esperti SAGE che supporta il governo britannico, la conoscenza del grado di incertezza sulla stima di R(t) è fondamentale per informare nel modo migliore possibile le decisioni politiche.
Simone Cialdi ha formulato il modello, stimato i parametri e calcolato R(t). Chiara Sabelli ha curato l'editing dell'articolo, la visualizzazione dei dati e la stima di R(t) sulla curva nazionale usando il metodo dell'ISS.
Ringraziamenti: Simone Cialdi ringrazia il Prof. Carlo La Vecchia per i suggerimenti e il supporto.
* Aggiornato il 25 gennaio alle 9h30. In una precedente versione di questo articolo veniva fornita una spiegazione spagliata sui motivi che hanno causato la sovrastima dell'R(t) della Lombardia per la settimana dal 4 al 10 gennaio.
Appendice
In questa sezione mostriamo i passaggi matematici che ci permettono, a partire dalla formulazione standard del modello SIR, di utilizzare la curva delle terapie intensive per la stima di $R(t)$.
Per prima cosa ricaviamo l’equazione per $R(t)$ ottenuta con il metodo descritto da Battiston partendo dal modello SIR. Quello che ci serve è l’equazione differenziale per il numero degli infetti $I(t)$. Questa equazione ha un termine di crescita che dipende dal numero di nuovi casi $C(t)$ e un termine di perdita che dipende dal fatto che i malati guariscono o muoiono:
\begin{equation} \frac{dI(t)}{dt} = C(t) - \frac{1}{\tau}I(t) \end{equation}
Il numero di nuovi casi $C(t)$ è proporzionale al numero di suscettibili $S(t)$ tramite due fattori. Il primo è il numero di contatti effettivi che ciascun suscettibile ha nell’unità di tempo; chiamiamo questo fattore $\beta(t)$ e lo definiamo così $\beta(t)=\tilde{R}(t)/\tau$, dove $\tilde{R}(t)$ è il numero di riproduzione netto relativo agli incontri e $\tau$ è il tempo medio dell’infezione. Il secondo fattore è la probabilità di aver incontrato un infetto, ovvero il rapporto tra il numero degli infetti $I(t)$ e il numero totale di individui della popolazione $N(t)$. L'equazione differenziale che governa l'andamento degli infetti è dunque:
\begin{equation} \frac{dI(t)}{dt} = \frac{\tilde{R}(t)}{\tau}\frac{I(t)}{N(t)}S(t) - \frac{1}{\tau}I(t) \end{equation}
Adesso poniamo $R(t)=\tilde{R}(t) S(t)/N(t)$ e otteniamo la relazione seguente:
\begin{equation} \frac{dI(t)}{dt} = \frac{R(t)}{\tau}I(t)- \frac{1}{\tau}I(t) = \frac{R(t)-1}{\tau}I(t) \end{equation}
Da notare che è $R(t)$ l’indice che ci interessa e che viene abitualmente calcolato e non $\tilde{R}(t)$. Infatti $R(t)$ tiene automaticamente in conto anche l’effetto dovuto alla riduzione dei suscettibili dovuta al diffondersi della malattia o all’effetto dei vaccini. È anche importante dire che per il metodo che stiamo descrivendo non è affatto necessario imporre l’approssimazione $S(t)/N(t)$ circa 1 perché il nostro fine non è quello di risolvere l’equazione differenziale.
L'equazione che abbiamo appena scritto ci permette di trovare il valore di $R(t)$ a partire dall'andamento del numero di infetti $I(t)$:
\begin{equation} R(t)= 1+\tau\frac{1}{I(t)}\frac{dI(t)}{dt} = 1+\tau\frac{dln\left(I(t)\right)}{dt} \end{equation}
Idealmente, nelle equazioni scritte $C(t)$ e $I(t)$ sarebbero rispettivamente i nuovi casi reali e gli infetti realmente circolanti. In pratica, però, nell’implementazione del metodo viene usato il valore degli infetti registrati $IR(t)$ e quindi in generale si ottiene un valore di $R(t)$ diverso da quello reale.
Veniamo adesso al nuovo metodo che proponiamo per la stima di $R(t)$. Facciamo subito notare che siamo autorizzati a sostituire nell’equazione per $R(t)$ la funzione $I(t)$ con la funzione $k\,I(t)$, dove k è una costante qualsiasi. Questo è possibile perché nell'equazione per $R(t)$ compare solo la derivata rispetto al tempo del logaritmo di $I(t)$ e questa è uguale alla derivata del logaritmo di $k\,I(t)$. Questa identità è ciò che ci consente di usare il nostro metodo:
\begin{equation} R(t)= 1+\tau\frac{dln\left(I(t)\right)}{dt} = 1+\tau\frac{dln\left(k\,I(t)\right)}{dt} \end{equation}
Per costruire il modello che ci permette di stimare $R(t)$ a partire dal numero di persone con COVID-19 ricoverate in terapia intensiva, che indichiamo con $TI(t)$, cominciamo stabilendo una relazione fra la curva degli infetti a quella delle terapie intensive
\begin{equation} \frac{dTI(t)}{dt}=\frac{q}{\tau}I(t)-\frac{TI(t)}{\tau_{TI}} \end{equation}
dove $q$ la probabilità che una persona infetta venga ricoverata in terapia intensiva, $\tau$ è il tempo medio dell’infezione e $\tau_{TI}$ è il tempo medio di permanenza in terapia intensiva. Partendo dall’equazione sopra si può ricavare il numero di infetti molto facilmente:
\begin{equation} I(t)= \frac{\tau}{q}\left(\frac{dTI(t)}{dt}+\frac{TI(t)}{\tau_{TI}}\right) \end{equation}
Le curve $TI(t)$ e $dTI(t)/dt$ si ricavano dai dati disponibili. L’unica accortezza è che l’incremento giornaliero delle terapie intensive, cioè $dTI(t)/dt$, deve essere trattato con cura. Infatti il numero è piccolo e quindi molto fluttuante, quindi meglio usare uno smoothing pesante (ad esempio una media con peso gaussiano con larghezza di almeno 15 giorni o anche uno smoothing di tipo adattivo). Da notare che le grosse oscillazioni che si trovano nella stima di $R(t)$ fatta con questo metodo nel periodo estivo sono dovute non al basso numero di terapie intensive ma al termine relativo all’incremento delle terapie intensive. Una volta ricavato $I(t)$, applichiamo il nostro metodo per ricavare $R(t)$. La prima cosa da notare è che non è necessario conoscere $q$ per ricavare $R(t)$:
\begin{equation} R(t)= 1+\tau\frac{d}{dt}\left[ \frac{\tau}{q}\left(\frac{dTI(t)}{dt}+\frac{TI(t)}{\tau_{TI}}\right)\right]= 1+\tau\frac{d}{dt}\left[\frac{dTI(t)}{dt}+\frac{TI(t)}{\tau_{TI}}\right] \end{equation}
La stima di $R(t)$ dipende quindi da due parametri. Uno è $\tau$, di cui abbiamo già parlato, e l’altro è il tempo medio di permanenza nella terapie intensive $\tau_{TI}$. La stima da noi usata per $\tau$ è di 9 giorni4, mentre per la stima di $\tau_{TI}$ possiamo partire dall’equazione per $TI(t)$, che può essere riscritta così:
\begin{equation} \frac{dTI(t)}{dt}=\frac{q}{\tau}I(t)-\frac{TI(t)}{\tau_{TI}}=\frac{dTI^+}{dt}-\frac{TI(t)}{\tau_{TI}} \end{equation}
dove il termine $dTI^+(t)/dt$ rappresenta i nuovi ingressi in terapia intensiva. Avendo a disposizione i dati sui nuovi ingressi in terapia intensiva potremmo ricavare direttamente una curva proporzionare a $I(t)$ da sostituire nell’equazione per $R(t)$. Tuttavia, questi dati relativi sono stati resi pubblici solo dal 3 dicembre in poi, dunque ci basiamo sulle ultime 7 settimane per la stima di $\tau_{TI}$ . utilizzando la seguente relazione che ricaviamo dall’equazione precedente
\begin{equation} \tau_{TI}= \frac{TI(t)}{\frac{dTI^+}{dt}-\frac{TI(t)}{\tau_{TI}}} \end{equation}
da cui risulta $\tau_{TI}$ =15 giorni per l’Italia (da notare che la stima di $\tau_{TI}$ cambia da regione a regione nel caso della sola Lombardia ad esempio è di 20 giorni). Nella figura sotto mostriamo il risultato della stima di $R(t)$ che parte dalle terapie intensive e la confrontiamo con quella basata sulla curva degli infetti e quella dell'ISS. Riportiamo anche la curva del numero di pazienti con COVID-19 ricoverati in terapia intensiva (linea viola tratteggiata) che mostra come il metodo diventi affidabile solo quando il numero di pazienti in terapia intensiva è sufficientemente grande.
